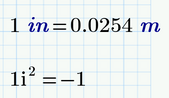Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Normalized intensity on value I(0)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Normalized intensity on value I(0)
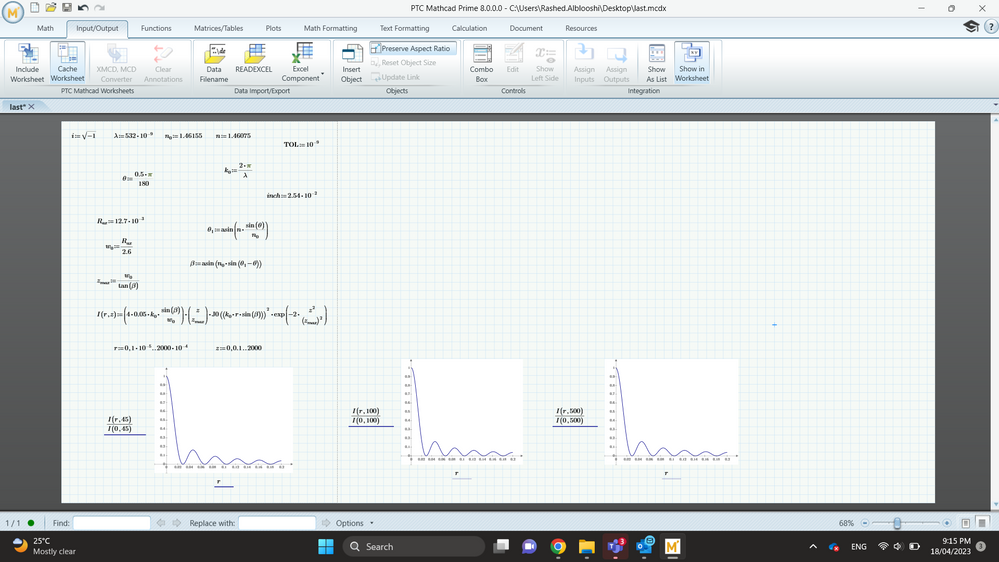
I have generated three plots for different z or distance
now i would like to compare the width of axial maximum and the width of central maximum is the value r from 0 to the point where the cure achieves zero.
I want to normalies and assume the value achive r=0
and i want to divide all values of I of I(r=0) how its possible to do this in mathcad
please help!
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One additional remark because you initially wrote that you are looking for "the value r from 0 to the point where the cure achieves zero. ".
The zeros correspond with the zeros of the Bessel function, divided by the factor you used for r in J0. And of course they are independent from the value of z.
Here are the first two positive zeros of your function - they correspond to the first two negative zeros of J0 because your factor sin(beta) is negative:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
and i want to divide all values of I of I(r=0) how its possible to do this in mathcad
Simply do it as you wrote.
In the plot at the placeholder for the function you simply type in I(r,100)/I(0,100) instead of just I(r,100).
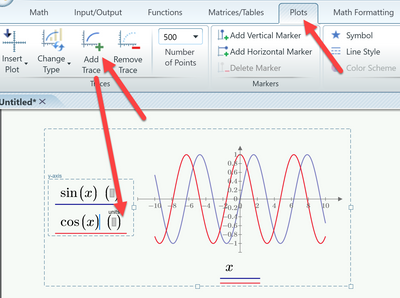
You may also plot all three graphs in one plot region using different colors. Guess you know how to add a second and third trace by either using the menu or by just typing Shift-Enter.
For further questions I would suggest that you attach your worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried this but still i cant see any difference they were all the same i will upload all the note , and please tell me how can i combine all three in one ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
About adding further traces
Its also not wrong to consult the help
When I asked you you attach your worksheet, I did not mean you to send a full screenshot picture but rather meant that you should attach the Prime file itself. You can do it by drag and drop or by browsing:
EDIT: I just look at the definition of your function I(r,z).
Changing z does just mean a scaling in ordinate direction. So when you "normalize" by dividing by I(0,z) you get the exact same function/graph, basically you cancel al the factors and what you see is the square of the Bessel function J0(k.0*r*sin(beta).
So of course you could not see any difference if you plot all traces in one plot - they are exactly the same!
Just a notice:
Prime can do quite well with units - You should use them!
No need to define units like inches and no need to define the imaginary unit (you get it by typing 1i or 1j without a space or multiplication inbetween)
Admittedly it looks ugly because on contrary to real Mathcad Prime does not suppress the leading "1" when it displays non-real numbers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One additional remark because you initially wrote that you are looking for "the value r from 0 to the point where the cure achieves zero. ".
The zeros correspond with the zeros of the Bessel function, divided by the factor you used for r in J0. And of course they are independent from the value of z.
Here are the first two positive zeros of your function - they correspond to the first two negative zeros of J0 because your factor sin(beta) is negative: