- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Numerical Solution for Bessel Equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Numerical Solution for Bessel Equation
Hello folks,
I'm trying to solve the Bessel equation that arises from the heat transfer equation of a straight triangulat fin. I know the analytical solution, but need to calculate the numerical solution for comparison purposes.
At the tip of the fin we know that dT/dx=0 and that at the base T(x)=Tb. I've tried using odesolve but it cannot solve the equation, so I'm thinking that odesolve is not the right solver, but do not know which one I should use. In this case, I placed the origin at the tip of the fin to simplify the differential equation.
Please take a look at the attached file for additional details
Any suggestions or recommendations would be greatly appreciated.
Thanks!
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try pls to solve it (without units) in Mathcsd 15?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
I had tried it before but was not getting anywhere. I finally was able to find the problem: dT/dx =0 @ 0 does not converge so instead had to change the left boundary of the domain to .000001 instead of 0, that is, dT/dx = 0 @ x = .0000001 instead of 0.
Thanks for the help.
FYI, in Mathcad Prime 3.0 we can find the same solution without anyother problems. Units cannot be used, though.
Regards,
Josué
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sometime I use not the built-in but user rkfixed function: I can see a part of solution
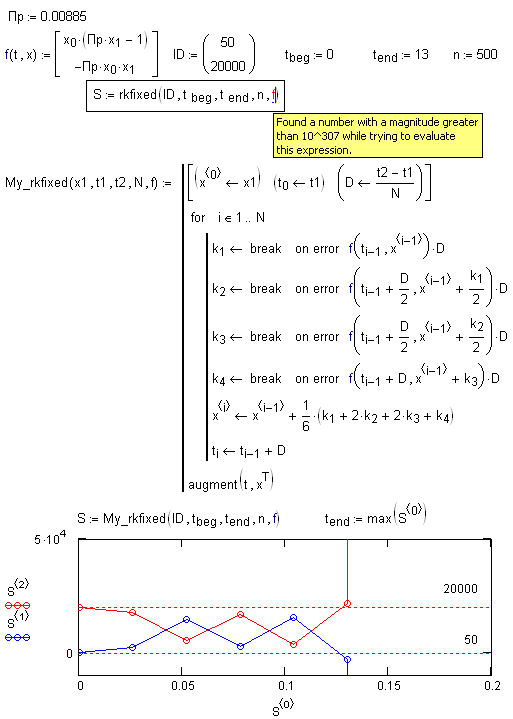
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Josue,
It is a good example for the new edition of this book - a solution is nothing, a way to solution is all!
http://www.springer.com/engineering/computational+intelligence+and+complexity/book/978-3-540-20852-5
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
Thanks for sharing your program for a user-defined alternative to rkfixed.
What actually makes this problem interesting is the boundary condition definition at the fin tip. From the analytical solution (and practical meaning of it), we use the bc θ(0) = finite, which eliminates the Bessel function of the second kind from the solution. We also refer to this bc as dθ/dx = 0, but in reality dθ/dx IS NOT 0.
So I think that a discussion in detail about this phenomena would be worthwhile, especially if we consider that Mathcad does not accept a boudary condition definition of finiteness, which would be the correct definition of the boundary condition, at least in my opinion.
Anyway, thanks again!
Best,
Josué





