- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
ODE Solve Blocks with conditional statements used to switch equations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ODE Solve Blocks with conditional statements used to switch equations
Werner;
The attached worksheet outlines my ultimate goal. This structure of the equations or requiems are called upon when particular conditions are met as shown on the diagrams and accompanying mass balance equations. This stormwater control structure is called a high early discharge tank. As you can see the tank has two chambers which become active when the water rises to particular levels in the first and second tanks. These different flow requiems which you have help me solve previously but this time all this knowledge needs to be stitched together. Unfortunately as you can see by the diagrams these must be switched on at certain times. Can you do this using a complex solve block? I thought one may be able to use an if statement in the solve block but this seems like it is not allowed. Is there another way to accomplish this for example can solve blocks become part of a programming block? What do you suggest? See the later parts of the worksheet for explanation.
You have been so helpful to me thus but once we solve this problem then my goal is achieved.
Kind regards, Mark
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your still QSCout still looks very suspicous. Not sure what you have in mind with the interpolation you suggest, but it sounds like a big botch. So why not just use Qpipe for the whole range - I guess it won't effect the maximum flowrate you obviously are after. At least unless you succeed in putting those equatoons right. Flowrate shouldn't change apruptly in my opinion and so the values at the end of the different ranges should match. Maybe there is some kind of correction factor you can apply?
In yor new QSCout there is a new discrepancy as of your habit of using the same name for differnt things - you are using h_LC in the routine which is not available here (and also Ithink should not be used here). But h_LC is not only the function for the water height in the main chamber, its also a variable you have defined somewhere, a very small lenght of 1um.
I think the large chamber does empty itself see the revised worksheet.
??? No, it obviously doesn't do so now. there remains a height of about 10cm at then end.
The length of that pipe is only the thickness of the barrier wall but the way the functions are being called it is the same length as the outlet pipe. It would be silly to rewrite these functions but I don't know how to pass a revised length back to the velocity function. As you see
No I don't and I won't bother looking at those lengthy calculations in detail. But gererally speaking - if you want a calculation being doen for different values of a variable, you will have to turn the whole calculation in one function/program. You have to know which argumetns that function must have.
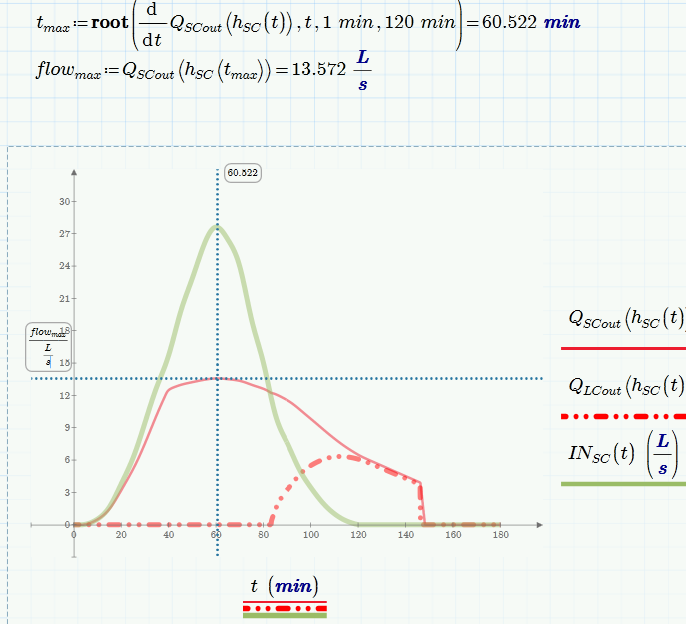
The last and final problem is a way to auto place a horizontal marker to show the peak discharge. As you can see from the final graph I am doing the placement manually because for some reason if I use Qscout(hsc(t) in the place holder I get an error.
Huh!?? What value of t you would have provided when you tried this?? Its silly, but those markers are not allowed to contain any units. So you may place QSCout(58min)/(L/s)in that marker placeholder. But first you would have to solve for the max time. One way is a differential appraoch like the following
What really bothers me is why the solve block fails if I slightly increase IN_SC(t). If I use the sheet use posted in your last reply I am not able to increase that inflow for more than 1.5% like so:
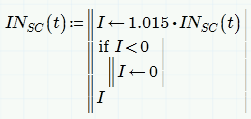
If I enlarge the length of the main chamber (L_t=20m, L_LC=19m) I am able to increase the inflow INSC up to 45%, then the solve block fails again. I am not sure why it is sfailing, but as changing the main chamber size affects it, I suppose it has soemthing to do with QLCout.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess I have to give up, things are going to confusing for me.
Just some last remarks concerning your last solve block:
h is parameter of the solveblock function, so it must be either a constant value or a known function when it is passed as argument later. You pass 15mm, so its a constant. But in the block h is first treated as function and even worse as a function which is subject to change - you gave an ODE for h(t) and even an initial condition, but you don't solve for it. And to top it you use a line later h again as a constant scalar as parameter for Qwinflow. So what did you have in mind for h: known constant, known function, function to be solved for, constant argument for Qwinflow,...???
Also problem with hw. First you use it as a constant (if hw<Spilllevel) and then as a function to solve for.
It seems to me you are searching for two functions at the same time and your solve block needs no argument. You also have to define the derivatives of those functions for the whole range of time.
I see vaguely from the pictures and textbook snippets you provide what you may be after, but I don't recognize it in your solve block. I also guees the meaning of h has again changed, its not the water height above exterm weir anymore, But then I may be missing the point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner;
I think I now know how to solve this problem at least conceptually. I don't think I need to couple ODEs in the solve block or try to incorporate tricky if statements to swap which equations the solve block needs to calculate at a given point in time. This is strategy is probably not even possible with Mathcad? So as you suggested I went through the worksheet and harmonized the variables. You were correct I was using different names for the same variable and I also had many redundant equations. It is surprising to me that the sheet worked at all. Lesson 1 be more meticulous.
Another surprise is that the cleanup didn't seem to alter the answer so I think I was simply using slightly differnt but redundant versions of the same equation. So here is what I think the solution is:
What I have to do is calculate the time at which the water spills over the internal weir. We already know how fast the water is rising in the first chamber (smallest tank). Next thing we know is the height of the spill level from the base of the tank i.e. the spill level creates a weir connection to the second tank chamber. The trick is that the water continues to rise over the barrier between the 2 chambers and thus creates the weir. The increasing depth above the weir then creates higher inflow to the large chamber (second tank). As you will see I have an array called X which is the depth of water at the weir location i.e. the height above the spill level.
The problem is one has a depth array but we need accompanying times at which these depths occur i.e. a time array. Once you calculate the time and knowing the depth then you can calculate the flow at each depth. Flow rate vs time array is a hydrograph (albeit a much smaller one than the main inflow hydrograph) which can then be routed to the second chamber i.e. water spills to the large chamber taking volume from the smaller chamber.
The problem is I do not know how to input multiple depth levels into solve block so that it can calculate the times at each depth level over the weir. I have an array of depths at the barrier location called X which I need to feed to the solve block so it can spit out the time array. However, my many attempts at this have failed. Is their a way to do this? See my X array and hw(t) function I have assigned hw(t)=X so that t can be calculated but for some reason this fails. Can you fix this and/or explain how this can be done?
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Haven't looked at the sheet but from your description it sounds like you are trying to mix a continious, functional approach (beginning with the interpolation of inflow values to turn it into a function, up to solving the ODE for the height in the first chamber) with a discrete approach, using kind of a lookup table, vector. This may be a discrepancy hard to follow. I can image that either a discrete or a continuos appraoch might work from the very beginning, but I doubt about the mixture. I have not the time to play around with the sheet at the moment but for the functional appraoch you sure have a pair of coupled functions and you will have to solve fo both at the same time (two compartnent problems) - being it Outflow_of_chamber1 & Inflow_to_Chamber2 or the heights in both chambers. Both function will be coupled by the height Hw and the valve betwen the two chambers. Not sure if you can look at the two chambers as one bigger chamber when the hydrograph is falling and both chambers are emptying.
So working with if-statements seems inevitable, but they do not belong in the solve block but in the definition of the functions in play. So one way could be to setup Hm(t) as a Hm(t, Hf) and use it in the solve block as Hm(t,Hf(t)). Not sure if that will work as expected, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is one has a depth array but we need accompanying times at which these depths occur i.e. a time array.
Thats not difficult to achoeve bu I am not sure if it would help you in your solution.

You should also avoid calculating hw(t) twice by assigning it to a variable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner;
This problem is much harder that I thought it would be. I think my approach can work but there is only a weak coupling between the small and large chambers. Also their hydrographs are shifted in time relative to each other which I don't know how to address with the solve block approach. I know you have already probably spent too much time helping me with this but I don't know if an alternative approach can overcome these problems. Can you have a quick look an give me some further guidance?
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, from your post I understand that emptying both chambers is not that easy to as we can't see them as one big chamber. See below - 5)
Can you explain in detail the function A(h). From a prior sheet I know something about a trapezoidal shape but its unclear how exactly the tank shape would be and especially how it would look like with the separation between forst and main chamber. I think I already wrote in a prior post about A(h) and
a) I dont understand the distinction between h<1m and h>1m
b) I think the formula for h>1m is wrong. What you have is obviously assuming a tank with rectangular base and sidewall with a slope. While you name Z slope Ithink the slope as I uderstand it it is 1/Z. Z=0 means vertical walls, the tank is a cuboid. The formula you provide is simply the volume of that tank divided by the height. This won't give you the top water area (unless Z=0) which I guess A(h) is supposed to provide. I think that A(h):=(W+2*h*Z)*(H+2*h*Z) is more appropriate. But that all changes again if the tank has a vertical wall separating first and second chamber. Or whatever the two chamber may look like - you haven't yet specified.
I won't bother dealing with the sheet you posted as on first sight it again seems to use a mixture of discrete and continous appraoch and not coupled ODEs.
But as I see it the task should not be that difficult. Each chamber has one IN- and one OUT-flow, the ones for the main chamber are coupled with the first, so we may also say that the first chamber has 2 in- and 2 outflows - we have to consider that in the ODE. So as far you are able to provide those four functions correctly and defined over the whole raange, covering all posibilities in one respective function (its those functions where all those if's should be in), the coupled system of two first order ODEs should be solveable (I hope). Don't bother with vectors and range variables if you follow this continous appraoch.
So we need the following and and I am using for the heights the names in the pictures you provide about first and main chamber. If you want to do us a favor you do so in your sheet likewise (or provide different labelled sketches covering the whole procedure from the first rain drop up to the empty tank again).
We need:
- a function A_f(H_f):=... for the first chamber (see my remarks above)
- a function A_m(H_m):= for the main chamber (see my remarks above)
- a funcion IN_f(t):=, the inflow in the first chamber (this already exists as interpolation)
- a function IN_m(H_f):= the inflow in th emain chamber = outflow from the first chamber over the weir dependent on the height in the first chamber. You have to define all functions for the whole range! So you would define something like OUT_f(H_f):= 0 if H_f<H_w, otherwise (formula which uses (H_f - H_w), the height over weir). Be sure to also cover H_m=H_f (better H_m>=H_f) also for H_m >H_w (that is water is still raising; not sure if there is a difference).
- a function OUT_m(H_m, H_f) describing the flow from the main to the first chamber. Of course this function would begin with "0 if H_m<H_f)". This function should give us the outflow from the main chamber to the first chamber and would be defined on the "weak coupling" between the chambers you describe in a manner you have to formulate. OUT_m() may also be dependent on the height in the first chamber (not only that its zeror for H_m<H_f) in as much as lower value of H_f might result in more water flowing from the main chamber to the first (less resistance ba the pressure in the first chamber, bigger valve opening?). YOu have to define the dependency.
- a function OUT_f(H_f); you already have provided that kind of function. (Q_out). I hope it still applies when the second chamber is in play. Can we simply add the OUT_m() to the volume in the first chamber? If no, you would have to change OUT_f() - probably adding H_m as second argument making it a OUT_f(H_f,H_m).
- Now all we would need are the two differential equations for H_f and H_m. As I see it they should be
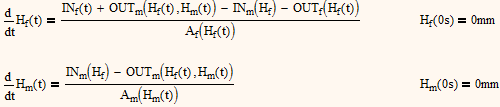
You have to solve for them at the same time as a system of ODEs.
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
Thank you for your detailed reply. It's late now so I will try what you have suggested tomorrow. As for the shape of the chambers you are correct they are boxes. I only used the prismodial formula to generalise the problem because often times this chambers are made from earth and side slopes of 1 in 4 are common in that case. A quick question to conclude is the format for coupling ODEs in a solve block the same as if you just have one ODE? In other words is the format within the solve block as you have shown? Lastly, you seem to be suggesting that provided the in and out functions are properly defined for the entire time of the simulation then you should be able to do everything in one solve block and not piece by piece as I tried to do is that a correct assumption?
king regard, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In other words is the format within the solve block as you have shown?
Yes, and you will put a 2x1 vector with both functions in odesolve(). I think I already posted a sheet solving for two functions in a prior thread of yours. You may look up the correct sytntax in the help, too.
Lastly, you seem to be suggesting that provided the in and out functions are properly defined for the entire time of the simulation
better "for all possibilities and combinations of the heights which are arguments", as none of those functions is directly dependent on time but just on the height(s).
then you should be able to do everything in one solve block and not piece by piece as I tried to do is that a correct assumption?
Yes, thats correct. Thats what I think we can achieve. You can't solve the problem piecewise in the manner first H_f, then H_m, because they are coupled. You could solve for t=0 to the time point where H_f=H_w. But from then on you must solve for H_m and H_f at the same time. This especially is true for the phase, when both chambers are emptying.
Afterthoughts:
As for the shape of the chambers you are correct they are boxes. I only used the prismodial formula to generalise the problem because often times this chambers are made from earth and side slopes of 1 in 4 are common in that case.
But you had Z:=1 in your sheet - so no simple boxes. No problem to generalize, but first again the question: What about that 1m limit in your A(h)???. Let both chambers share the same width W and the lengths are Lf and Lm. We assume one tank (length=Lf+Lm+divider_thickness) with sloped walls, Z being the reciproke slope value (Z=0 --> wall straight up, slope=infinity, boxes). The tank is divided by a straight wall across its full width (straight up,no slope). This would yield A(H,L):=(W+2*H*Z)*(L+H*Z). You can use the same formula for both chambers, simply call A(H_f(t),Lf) for the first chamber and accordingly with H_m(t), Lm for the main chamber. We don't need two different functions, but if you wish you could set it up with two separate functions (as demanded in my previous post) as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner;
I have simplified the chambers they are now two boxes. Which I call SC and LC.
In the drawn diagram provided previously f=first chamber. On my worksheet, however, f=SC which I call the small chamber. Also in the diagram m=main chamber which in my worksheet I m=LC i.e. the main chamber I call the large chamber. Other than that there concept is identical when your reading it whenever you see SC just think f and when you see LC just think m. I just think my names are more descriptive. Also, I adopted you IN notation for flows into a chamber but instead of your notation OUT I use Qout. Q means flow so flow out of the small chamber would be QSCout.
Your point 4. If we have a one way flap valve on the weir going from LC to SC then we do not need to consider HSC=HLC or HLC>HSC those cases. Flow will therefore only occurs when HSC>HLC and HSC>Spill Level else their is zero flow.
Your point 5. Again if we If we have a one way flap valve on orrifice pipe between the large and small chambers then only when HLC>HSC will flow occur from the large chamber (LC) to the small chamber (SC). No flow can go the other way i.e. from SC to LC by way of the pipe orifice between the chambers hence if HLC<HSC flow between the chambers is once again zer hence the else statement.
Your point 6. The QSCout applies to both chambers SC and LC as this is what drains both tanks once water level in the small chamber HSC<HLC or their heights are equalised i.e. HSC becomes equal to HLC. I am not certain if I have to do an if statement for this as the small chamber is draining all the time as it discharges first because it develops the highest water depth first and therefore has the highest initial outflow. It is only when HSC<=HLC that we get water being drawn from the large chamber i.e. LC.
Your point 7, I believe I have set up the coupled ODE's correctly however as you can see I have problem with my initial condition. I believe however that this MathCad error is not initial conditions but something else as at t=0s both the LC and SC have no water which is correct.
What may be the problem is the two parameter functions which I must admit I am not sure are necessary and maybe my inflow and outflow functions are not set up to cope with 2 parameters in fact I don't see a way to do this?
Hopefully you could have a look at what I have done to eliminate this error.
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
After a quick look (more in the afternoon (in my timezone)):
1) the functions in odesolve have to be in a vector, too.
2) Your INLC is definitely wrong. it uses a never ending recursive function cll, calling itself foreveer. It seems illogic to me, why you define SPilllevel (=height of weir wall) in this function and not along with the other dimensions. Also hSC>hLC looks wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner;
Once again thank you for looking at this for me.
Your point 1, I thought hSC(t) and hLC(t) are functions both of time. Are we not solving for these height functions by using the coupled ODEs? Maybe the coupled ODE syntax is incorrect?
Your point 2, INCL program block calls INLC(hsc):=C*L*(hsc)^1.5 which I tested with a range variable hsc:=0m,0.1m..2m and it works. However, I do agree that the logic "AND" probably should be an "OR", but as you are usually correct I wait for your more detailed response.
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The same name for different function is more than confusing - pleas not again!
Both QLout and INLCare are obviously using both heights, so both must be paraneters of those functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Whoops! Sorry QLout should be QLorifice. I changed this but still the Solve Block is not happy.
Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Buckton wrote:
Whoops! Sorry QLout should be QLorifice.
Which one and where?
Some things I noticed:
- Spilllevel (=height of weir wall) should be defined along with all the other variables like tank width, etc.
- You use L which (most of the times) should be unit liter, but its labelled as variable L which unfortunately exists and is 0.05 m. This yields wrong results and units.
- IN_LC (the first of the two): 1) shouldn't it be dependent on water height over weir (= h.Lc - spilllevel)?
2) it returns wrong units, no matter if L is unit(m^3) or varible (m)
- IN_LC(Hf,Hm)
if Hf<Hw (=spilllevel?) then 0
if Hf>Hw AND Hm<Hf then there is a flow from the first to the main chamber - weir. But is this also the same formula when both heights are above the weir height
What happens when the given Inflow is so big, that both heights raise above the weir wall. Both heights must be equal in that situation, but we have to deal with that situation in terms of mass flow equations. You have to define the mass flow from first to main chamber for this situation, too and I guess its not the same as the mass flow over the weir.
- Even if I use the correct sytax for odesolve and even as I corrected the wrong units in a crude way the odesolve block throws an "unknown error" and no possibility to race that error. Prime really is more than user unfriendly in that respect, too.
BTW, in the solve block Hf and Hm must be functions of time in every occurance. I missed that twice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Where there are 2 orifices one at the main outlet located in the small chamber. The one that I changed is the orifice between the large chamber and the small chamber water only flows from large to small chamber if the water level in the large chamber is higher than the level in the small chamber or the water levels are equal which would make both chambers to act as one. The equation QLCorifice is identical to the equation used for the final outlet. The only difference is that the final outlet also has a length of pipe connected to the orifice which restricts the outflow more than an orifice would
I agree Spilllevel is a tank component and needs to be defined in the variables section.
I Will have to look for these L variables because I try to make it a habit to subscript all variables.
YEs the water level in the small chamber needs to minus the SpillLevel to get a the depth over the weir barrier. I recall I did this previously but ran into problems but conceptually what you say is correct.
WAter is piped directly to the small chamber so I don't envisage that the large chamber would buildup above the slotted weir in the barrier wall. However if it did I have a flap valve which would close preventing water flowing from the large chamber to the small chamber by way of the slotted weir hence why I have the else statement which defaults to zero flow where a condition other than water in the small chamber is higher than the water in the large chamber. You could have 2 way flow but that overly complicates the situation and in my view is not necessary to take into account.
But is my solve block couple ODE syntax correct? I agree there error messages leave a lot to be desired.
Werner it goes without saying that I really appreciate your help on this matter and if I can give you an amazon gift voucher for your effort please let me know your details and I will send you a voucher. Contact me offline as you will find my email on the PTC address book.
KInd regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
WAter is piped directly to the small chamber so I don't envisage that the large chamber would buildup above the slotted weir in the barrier wall.
What I had in mind is: a large inflow to the first chamber, just a small outflow from the first chamber which can't cope with the inflow, water is rising in the first chamber up to the weir and begins flooding the main chamber where the water begins to rise. If the big inflow doesnt stop the water in the main chamber will raise up to weir and beyond. In my underatnding both chambers become one big tank now, no matter how wear or small the valve connection between he two chambers at the bottom might be. The weir wall is fully flooded and has no effect other than taking up small volume in the tank.
The way the model was set up is that the initial inflow ONLY affects the area of/above the first chamber which is not true in that case. So either we would have to change that approach or deal with the situation via the IN_LC function. In the latter case we would assume that its possible that (even though there is no wall and weir visible anymore) the height h_SC is getting slighty higher than h_LC. The superfluous water volume would then immedeatly(?) flow over to make h_SC=h_LC. But how do we get time into the game, how would be get a flow rate in L/s? Looks like we would have more than two ODEs to solve simultanously?? What do you think?
Is it really possible to calculate a flow RATE by simply knowing the heights in the two chambers??? I am beginning to doubt that. From where would we get the time?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe I am not fully grasping the concept of a weir, I wonder about the length of just 5 cm you defined.
Anyway here is the sheet which I cleaned up as good as i was able to. Unfortunately no success.
Look at the graphs at the end to see if they are realistic. Maybe the solver chokes on the discontinuities of the derivatives of the functions used. i don't know.
I also notice you had used h_SC quite often with different meanings. You may want to look if your function use the correct h_SC and may consider renaming. All this should have no influence on the odesolve, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So to (hopefully) finish it up - this really was a tough one.
I don't think that the function you provided are correct. I doubt about the step at 10cm in Q_SCout(H_SC) and especially I am pretty sure that your Q_LCout is wrong - for H_LC only slighty higher than H_SC I would expect a very low flow rate. Your functions doesn't take in acount H_SC at all.
I finally got the whole sh....eet to work but its pretty instable. If I only multiply all IN_SC(t) values by 1.1 the solve block fails again - probably because of wrong formulas(?) used. Multiplying by 1.05 works and shows, that h_LC can also rise above the spill level.
What did I change to make it work:
1) I assured that your functions will return 0 if a height is negative (which it will be and thats one reason the block failed)
2) I modified your Q_LCout so that your routine is fed with the height difference of the two chamber rather than just with the height of the large compartment. I don't think that this is correct, but it seems at least more reasonable than what you provided (see above). I don't fully understand what you do with your QSorifice, but I guess its a difference if two chambers, both filled with water, are connected by a valve, or if a chamber is emptied by a drainage. You use the very same formula for both.
3) I made a wrapper for IN_SC(t) to assure that only positive input is applied, negative values are set to 0. This is not absolutely necessary to make the block work but it seems to be reasonable and disabling that warpper shows a strange effect in that the large chamber never gets fully emptied - see yourself.
So now you have a working sheet and you can play around with the various functions yourself to hopefully find the best ones describing the physics behind the scenario.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner;
This is a marvelous result thank you. "I doubt about the step at 10cm in Q_SCout(H_SC)", your hunch is absolutley correct, this is a known problem. My understanding is that the problem occurs at the transition zones at certain flow reguimes because of the circular geometry such as pipes. There are actually 3 zones (circular weir, submerged oriffice and pipe flow) to simplify the problem I only used 2 zones. Orifice flow and pipeflow. However there is still research going on to work out where these zones start and end but they appear to change with flowrate. There is also a know problem of hysteresis loop forming creating a jump. If you are interested I have attached an Australian paper describing this affect.
"I am pretty sure that your Q_LCout is wrong" again you are correct because the downstream water level does effect upstream, that is to say that I have again used a simplification called outlet control where the discharge from the large chamber to the smaller one is independent of the water level of the small chamber i.e. its only controlled by the orifice however as you point out that is not correct and one must apply the Bernoulli equation (by Swiss mathematician Daniel Bernoulli) to get the correct solution.
I try to understand in depth what you have done and see if I can make the model more physically correct.
Thank you much appreciated.
Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner;
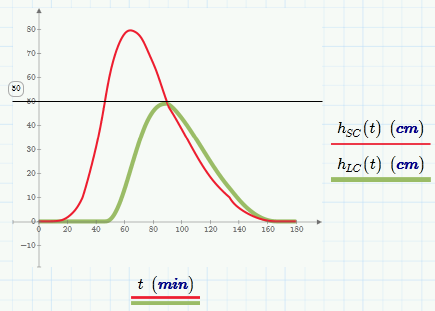
I have rationalized some of the variables used, cut some more redundant equations and added some additional logic and a new equation for circular weir flow.
I think the large chamber does empty itself see the revised worksheet. The last plot shows the inflow hydrograph for the rain, and for the small chamber and large chamber. The falling limb of the large and small hydrographs become coincident at about the 130 minute mark. Both chambers are empty as far as I can tell at about t=150 minutes. As you said this system of equations is very numerically unstable. For example if you increase the outlet pipe length Lp by only a small amount there will be no solution found. I believe it is all to do with the transition zones between weir, orifice and pipe flow. As I said I previously only used orifice and pipe flow requiems. I have now introduced the circular weir requiem. Although I am using the state of the art equations (from the latest journal articles) there is some weird transition stuff happening between the flow requiems and this is were I think the instability stems from. The only way to fix this I think would be to do a smooth curve fit of the piecewise equations but I don't know how to do this when these functions are dynamic as they are being called by the ODE solve block. The other problem the length of pipe that connects the large and small chambers. The length of that pipe is only the thickness of the barrier wall but the way the functions are being called it is the same length as the outlet pipe. It would be silly to rewrite these functions but I don't know how to pass a revised length back to the velocity function. As you see I started this by gave up as it just wouldn't work. The last and final problem is a way to auto place a horizontal marker to show the peak discharge. As you can see from the final graph I am doing the placement manually because for some reason if I use Qscout(hsc(t) in the place holder I get an error.
As for the results they look correct to me i.e. their order of magnitude seems in the "right ballpark". I you could help me with these final problems it would be much appreciated.
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your still QSCout still looks very suspicous. Not sure what you have in mind with the interpolation you suggest, but it sounds like a big botch. So why not just use Qpipe for the whole range - I guess it won't effect the maximum flowrate you obviously are after. At least unless you succeed in putting those equatoons right. Flowrate shouldn't change apruptly in my opinion and so the values at the end of the different ranges should match. Maybe there is some kind of correction factor you can apply?
In yor new QSCout there is a new discrepancy as of your habit of using the same name for differnt things - you are using h_LC in the routine which is not available here (and also Ithink should not be used here). But h_LC is not only the function for the water height in the main chamber, its also a variable you have defined somewhere, a very small lenght of 1um.
I think the large chamber does empty itself see the revised worksheet.
??? No, it obviously doesn't do so now. there remains a height of about 10cm at then end.
The length of that pipe is only the thickness of the barrier wall but the way the functions are being called it is the same length as the outlet pipe. It would be silly to rewrite these functions but I don't know how to pass a revised length back to the velocity function. As you see
No I don't and I won't bother looking at those lengthy calculations in detail. But gererally speaking - if you want a calculation being doen for different values of a variable, you will have to turn the whole calculation in one function/program. You have to know which argumetns that function must have.
The last and final problem is a way to auto place a horizontal marker to show the peak discharge. As you can see from the final graph I am doing the placement manually because for some reason if I use Qscout(hsc(t) in the place holder I get an error.
Huh!?? What value of t you would have provided when you tried this?? Its silly, but those markers are not allowed to contain any units. So you may place QSCout(58min)/(L/s)in that marker placeholder. But first you would have to solve for the max time. One way is a differential appraoch like the following

What really bothers me is why the solve block fails if I slightly increase IN_SC(t). If I use the sheet use posted in your last reply I am not able to increase that inflow for more than 1.5% like so:
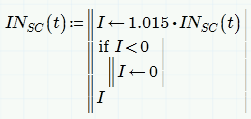
If I enlarge the length of the main chamber (L_t=20m, L_LC=19m) I am able to increase the inflow INSC up to 45%, then the solve block fails again. I am not sure why it is sfailing, but as changing the main chamber size affects it, I suppose it has soemthing to do with QLCout.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner;
Thank you very much for all your hard work on this problem it is much appreciated. As for the Large Chamber not draining you will notice from the hydrograph plots that flow rate from both tanks drops to zero at about the 120 minute mark. The large chamber does drain but it is acting under such a low head pressure that it takes up to 300 minutes i.e. it trickles out.
I think we will call this problem done. Unfortunately I don't know why it is so numerically unstable. I have found literature which gives me the best possible equations for the weir and orifice flow requiems and have largely eliminated the step in the Qscout rating curve but that doesn't seem to help the situation. I am sending this Worksheet to Professor Dixie Griffin he is a Civil engineer and MathCad user. Hopefully he will check if I have all the correct equations.
If I have then one can conclude that even MathCad's state of the art ODE solvers cannot solve some problems, or maybe our whole approach is wrong. I doubt it though as the mass balance which we have used is fundamental to solving thesetype of problem. Once Professor Griffin gets back to me I will update you on what he believes we must do to make this calaculation more stable.
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
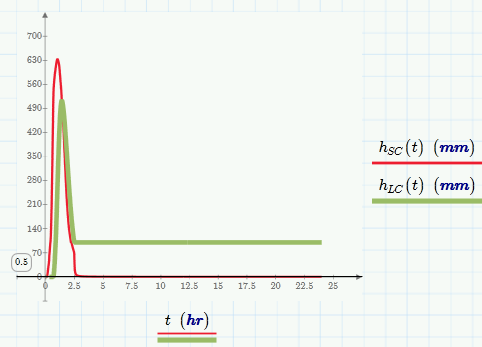
As for the Large Chamber not draining you will notice from the hydrograph plots that flow rate from both tanks drops to zero at about the 120 minute mark. The large chamber does drain but it is acting under such a low head pressure that it takes up to 300 minutes i.e. it trickles out.
Thats not reflected by the plot. As you can see in the screenshot below I let the simulation run for 24 hours and the water level in the large chambers stays constant.
BTW, if you try this the solve block will fail. This is because we have a rather huge time interval but only 1000 steps, so the algorithm goes havoc. We can cure this by demanding more steps - I found that 10^4 steps will make the block work again. Maybe worth a try in other cases where the block fails, too. Th number of steps is an optional parameter of odesolve()
![]()
I think we will call this problem done.
OK, so lets wait for other input.
I am sending this Worksheet to Professor Dixie Griffin he is a Civil engineer and MathCad user. Hopefully he will check if I have all the correct equations.
As far as I remember he is also a participant of this forum and I think I've seen a post from him here not long ago. So I guess if he would be interested he would probably had already joined this discussion, but then I may be wrong - we'll see and you will update the discussion here if appropriate.
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner;
It is great you found out about this optional parameter for the ODE solve block, thank you. As for the emptying the large tank, I forgot that I was using a slightly modified version of the worksheet that I had uploaded. As you had suggested I removed the orifice equation (I think your actual suggestion was just to use the pipe flow requiem). This simple change seemed to "let the water flow" from the large to the small tank and drain the system but as I said it takes much longer than 120 minutes.
Instinctively, I believe we are getting the correct answers but everything I read says you must consider the three flow requiems (weir, orifice and pipe) but as you have seen even though I seemed to be using he best empirical equations available there still seems to be a discontinuity between the flow requiems. There is a closed form solutions for circular weir and orifice flow but it involves elliptic equations which are very complicated and need look up tables to solve the various parameters and so from what I read are impractical for engineering purposes.
As you say lets see what Professor Griffin says about what we have done, my belief is that the procedure is correct but I think the Civil Engineers may do some trickery to make the problem more tractable.
Kind regards, Mark





