OFDM Signal Reconstruction via DFT

[ptc-5008524]

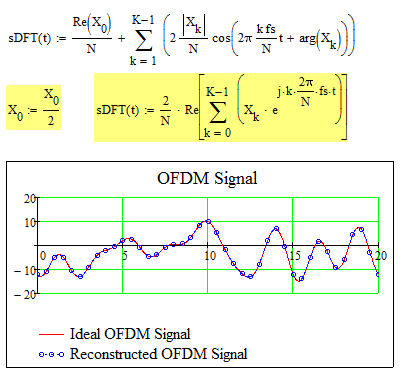
I'm having trouble reconstructing an OFDM QAM signal using its amplitude and phase spectra obtained by using the DFT. The QAM signal is given in the image below.

I have tried to do it so far using the below equation.

This is the closest I have reconstructed it to the original. What am I missing?

I am using Mathcad 13.

[Werner_E]

You sure would get a better respones if you attach a worksheet. From the pic alone probably nobody would be able to determine what the problem ould be.

Would the following link be of any help?

http://www.comlab.hut.fi/users/tko/geta07/GETA fall 07- OFDM with MathCAD.ppt

[ptc-5008524]

No sorry that doesn't help. I was browsing through that just last night actually. I have attached my worksheet.

[Werner_E]

Jonathan Mayers wrote:

No sorry that doesn't help. I was browsing through that just last night actually. I have attached my worksheet.

Was just a try.

So hopefully someone with better technical background could jump in.

BTW,

• are you sure about the absolute value of X0 in the definition of sDFT(t)?
• could it be that you used the wrong vector X in the last definition? You redefined X in the Spectral Analyisis section.

[ptc-5008524]

1. Yes. The DC value is part of the reconstruction.

2. No. The last definition of X is what I'm supposed to use.

[Werner_E]

Jonathan Mayers wrote:

1. Yes. The DC value is part of the reconstruction.

2. No. The last definition of X is what I'm supposed to use.

OK, so I'm not of much help. It was just that I thought that

1) the DC value could be (is) negative!?

and I noticed that

2) you are using just the first 10 values of the 200 element vector X in the definition of sDFT for reconstruction. Obviously thats supposed to be done.

[ptc-5008524]

Yes because after the first K components, all others are zero and do not affect the calculation. The DC value is positive for me so I'm not sure what you mean. However, I changed the equation up a bit and instead I put my DC value to be negative and the two signals overlay exactly. For anyone who may be in a similar situation, find attached the mathcad 13 worksheet.

[Werner_E]

Ah yes, that makes sense, especially if you think of the reconstruction in its complex form

BTW, I think your DC should be X0/N (without the absolute value) or even better Re(X0)/N so you are prepared if cause of numeric errors you get an imaginary part in X0.