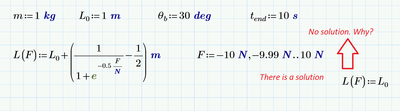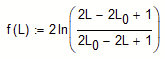Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Odesolve problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Odesolve problem
See Prime 6 in attach (one pendulum with a ribbon)
- Labels:
-
Calculus_Derivatives
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
See Prime 6 in attach (one pendulum with a ribbon)
Looks like you forgot to attach the file!
BTW, how could L(F):=L.0 be a solution? Given the function L seen in your screenshot this seems to be not possible. F=0 is the only value for F where L(F) would be L.0. Or did you mean something else?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry ~ see the attach Mathcad 15 and Prime 6
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Strange and quite sensible. Usually this could mean "check your equations"?
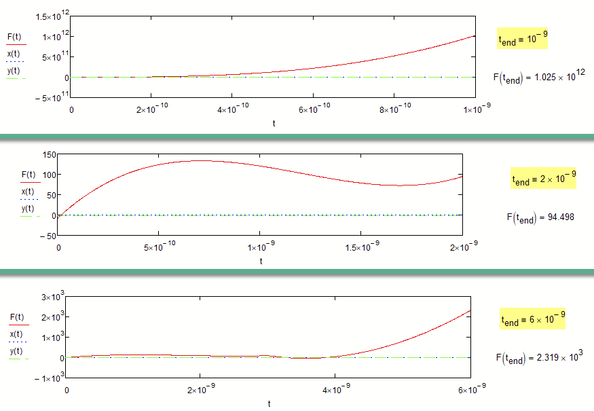
See here the result with three different end-values and notice the magnitude of the force values.
Force seems to be rising and positive in these scenarios but the error thrown ("number with magnitude greater than 10^307) when calculating L(F(t)) would only occur if F goes below -1413 ?????
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So the initial force F(0) is zero in your approach?
Valery demanded it to be F(0)=-8.496 but so his first equation x^2+y^2=L(F)^2 is not fulfilled .
It looks like L exceeds the valid range from 0.5 to 1.5 during the solving procedure which results in wrong return values of your function f(L).
This is the reason the odesolve block fails when I replace your interpolating function f(L) by the symbolic inverse
as it would return non-real values which odesolve doesn't like at all.
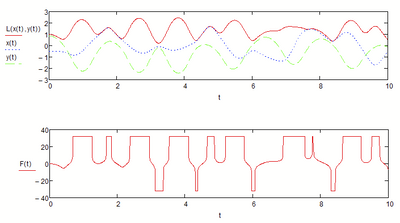
If I limit the range for L
also the force is limited
Not sure which approach fits Valerys problem better.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner, you are probably right. I took a fairly arbitrary approach, as it wasn't clear just what physical system Val was modelling!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@AlanStevens wrote:
Hi Werner, you are probably right. I took a fairly arbitrary approach, as it wasn't clear just what physical system Val was modelling!
I don't know either but it may have to do with this thread: https://community.ptc.com/t5/PTC-Mathcad/New-problem-with-circles/td-p/780229
Your answer reminded me that we often had problems with an odesolve block when trying to solve for a function for which there was no ODE (like here with F(t)). It was then necessary to pull out that function from the odesolve like you did and this often meant to use quite "creative" (and sometimes awkward) solutions.
I am not sure why Valery had chosen the initial Value for F(0) the way he did.
I tried with the "correct" initial value F(0)=0 but the solve block still failed. "Correct" according to his initial values for x and y and the first equation.
Maybe the problems occur because his function L(F) isn't an appropriate model for an elastic rubber band (infinite force -> still length 1.5 meter). Maybe it just means that the rubber band breaks 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or there is a 1.5 m titanium (or kevlar, or other strong stuff) rope in parallel to the rubber band....
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
Or there is a 1.5 m titanium (or kevlar, or other strong stuff) rope in parallel to the rubber band....
Luc
🙂
But then the force applied by the rubber band wouldn't change and again be limited, wouldn't it?