Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
One catenary problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One catenary problem
The description of the problem is here - http://communities.ptc.com/videos/1549#comment-11596
Help me please! My first step is in attach. Is it any right direction?
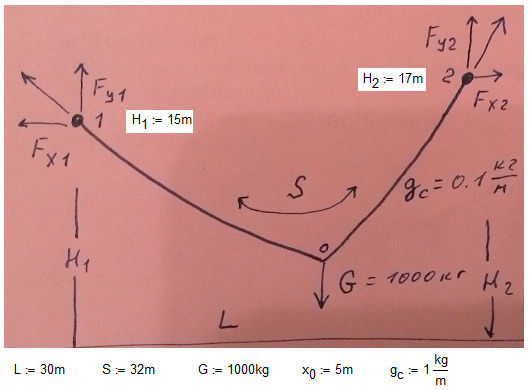
Solved! Go to Solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry but I see it this brench of PlanetPTC so:
Valery: I have one model and need one more equation. Help me please.
Werner: I feel that the model is wrong but have no time to point it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Where now is Tom Gutman? Does anyone know?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Arbiter 007 wrote:
Looks like he hasn't logged on in a couple of years:
http://communities.ptc.com/people/TomGutman
TTFN
Thanks, I have seen it too.
Can we call to the Phone on this page and ask someone?
Mr. 007 - it is any search work for You!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Arbiter 007 wrote:
Looks like he hasn't logged on in a couple of years:
http://communities.ptc.com/people/TomGutman
TTFN
I remember that at the time the collaboratory was moved over to this communities with all its problems, drawbacks and errors, Tom reported having big difficulties with login without getting any help from PTC staff. I am not sure but I guess he left in frustration.
A big loss for the forum anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
11 unknowns, 9 equations and no solution found 😞
Maybe we should not expect two catenaries.
Look if the chain has to hold a bridge - at equidistant points we may apply vertical ropes to hold the weight- This time we don't get a catenary but a parabola!
Sorry.
It is not a parabola but a set of catenaries (chains) with a form of parabola.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Werner Exinger wrote:
11 unknowns, 9 equations and no solution found 😞
Maybe we should not expect two catenaries.
Look if the chain has to hold a bridge - at equidistant points we may apply vertical ropes to hold the weight- This time we don't get a catenary but a parabola!
Sorry.
It is not a parabola but a set of catenaries (chains - near line) with a form of parabola.
I have checked it myself![]()

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have checked it myself
So you have seen its neither pieces of parabolas nor pieces of catenaries but just straight line segments 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If it is absolutely flexible catenery/chain placed between two attachment points, it takes the form of a catenary (hypercos). Builders do lengthes of the vertical suspension bridge cables such that the load of each vertical rope was the same. This leads to the fact that the attachment point pass through the vertical ropes parabola. But we have a catenery between the points curve, which is close to a parabola because the main two rope bridge is not absolutly flexible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If we can image an absolutely flexible chain we also can image making the distance between the vertical ropes infinite small. Its only that way we get the parabola of course.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
11 unknowns, 9 equations and no solution found 😞
More two equations - balances x and y forces in the point 0.
Tomorrow I will try to do it. Now I go to bed. In Moscow 22:40
Werner and Mikko - you have more 2 hrs (20:40) for do it before go to bed ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it is one more equation we needed:
:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you state c=c, then B1&B2 are known due basic geometry and load position.
A1&A2 are unknown, but dependend, thus leaving us with one equation and one variable?
Also load point must be on catenary, which gives us one extra condition for system of equations.
Maby you have a point here... ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mikko Hinkkanen wrote:
If you state c=c, then B1&B2 are known due basic geometry and load position.
A1&A2 are unknown, but dependend, thus leaving us with one equation and one variable?
Also load point must be on catenary, which gives us one extra condition for system of equations.
Maby you have a point here...
Mikko,
when can we see your own Mathcad sheets or edited our?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's hard to impove pavement laid by masters, but I try to contribute something later. Honestly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mikko Hinkkanen wrote:
It's hard to impove pavement laid by masters, but I try to contribute something later. Honestly.
You welcome, Mikko!
One fresh man - one fresh solution!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One fresh man - one fresh solution!
Well, I don't know about freshness (newborn in house) but here is something (Prime 3) that you might consider either as good joke or a new direction in problem...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fine, Mikko!
1. See in attach my little correction (not Find but Root).
2. Now we/you can convert it in M15 and create an animation. But where ia the load? No animation - no solution!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Valery,
there is a solution for vertical point loads in the refrenced paper - so, there is some hope that it will be possible with Mathcad as well. Lets see if I/you/someone on community has some time to type it.
You seem to be very keen on animations. Personally I would like to see macro buttons in Prime 4.
EDIT:
yeah, root is much more elegant than find... this is what you get when using copy paste at end of day.
Message was edited.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In a catenary, the horizontal tension is constant.
You can develop enough equations to find a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
In a catenary, the horizontal tension is constant.
Yes - in the point 0 too
Thanks, Fred. I have lost my dream...
But change please H1, H2, G etc and see the plot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't see a problem. You can set up the solve block as a function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, changing the weight G from 10^-3 to 10^6 (the smallest and largest values allowed) does not affect the graph!??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
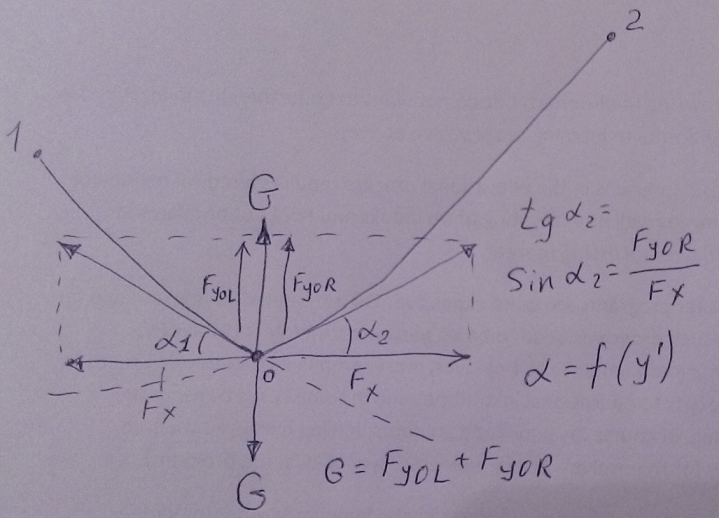
Werner Exinger wrote:
Hmm, changing the weight G from 10^-3 to 10^6 (the smallest and largest values allowed) does not affect the graph!??
The smallest value of G must be 0
The smallest value of x0 must be 0 too etc
We must create 11 equations with 11 unknowns and try to solve it.
But I think Mathcad cannot solve it. We must put fine guess values.
But let we try.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
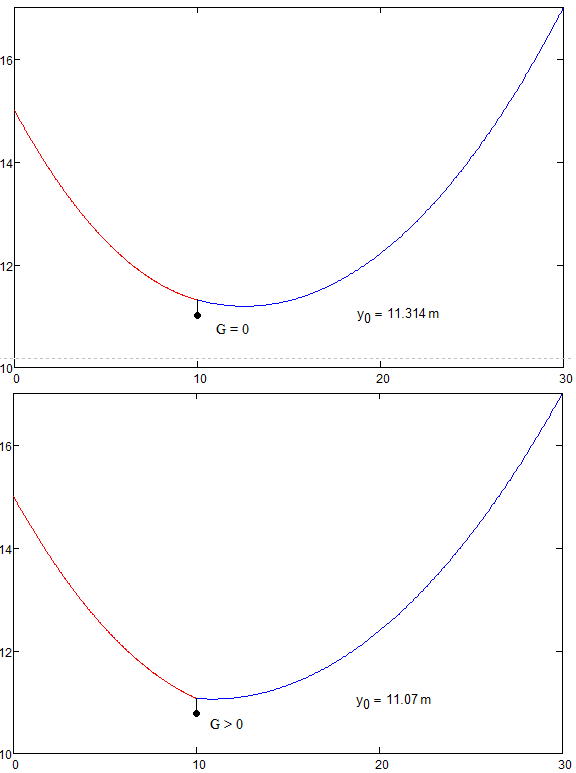
You'll laugh, but there is any solution!
Check it please!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great job Valery!
A humble Thank You!
Solution seems to be stabile even with one real case with:
- H1=16m, H2=11,75m, L=126, S=129, G=240kg, gc=0,41kg/m
Now, back to problem set - "elastic catenary with point load". We are on halfway of our journey... ![]()
Hints:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See the video here http://communities.ptc.com/videos/4417
But the solution is not stabile - catenary-arch-catenary-arch etc
We must think about more good guesses. Use for example in new step solution of the last step.
And no problem with elastic catenary...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
We must think about more good guesses.
Not so crazy catenary with load.
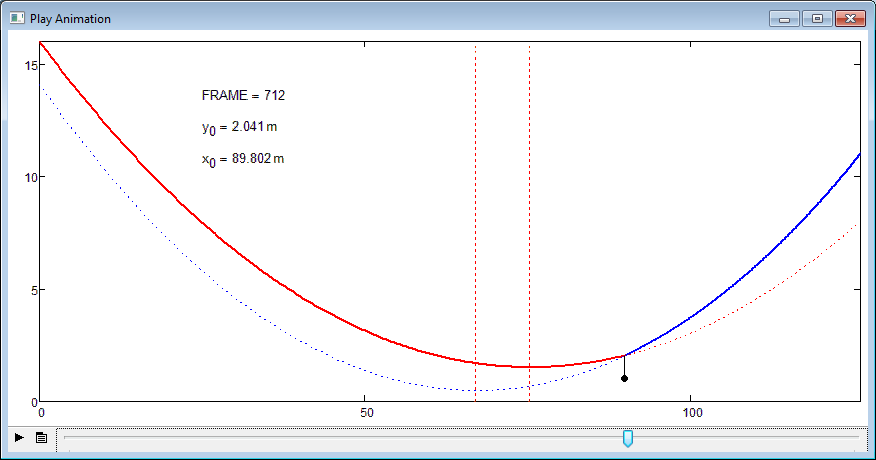
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is nothing so aggravating as a good-looking wrong answer!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
There is nothing so aggravating as a good-looking wrong answer!
The best answer on a good-looking wrong answer is one good-looking correct answer! ![]()





