Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
One catenary problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One catenary problem
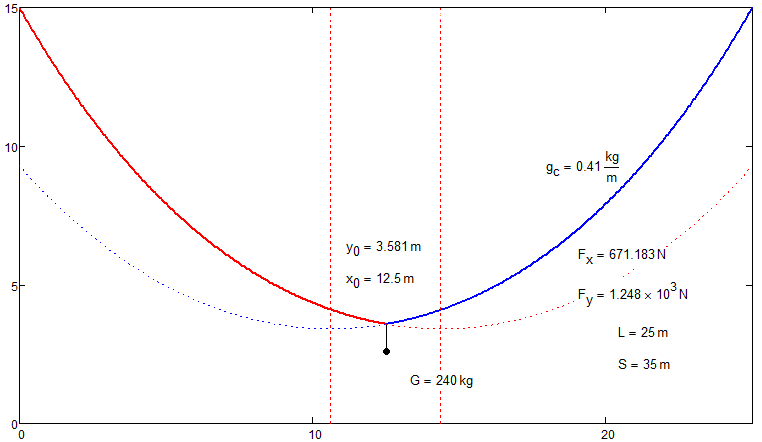
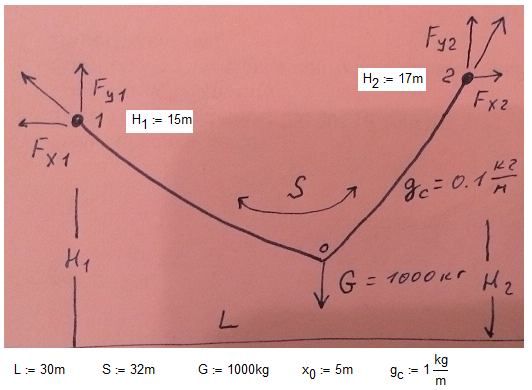
The description of the problem is here - http://communities.ptc.com/videos/1549#comment-11596
Help me please! My first step is in attach. Is it any right direction?
Solved! Go to Solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Welcome, Leopold!
We have a catenary but you have in Australia an arch ![]()

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
???????? Posting just to post or am I missing the point? Its a catenary, yes - or better an approximation of such - but so what? Or is it supposed to be funny - how??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry Valery, thats the Gateway Arch in St Louis, Missouri, U.S., not Australia (yes I know, you were thinking of upside down, down under, etc.).
The Gateway Arch isn't a normal catenery at all. The normal catenery would be the most efficient shape if the the thickness of the arch would be the same all over. But the cross sectional area of the Gateway Arch is about 125 ft^2 at the top, but 1263 ft^2 at the bottom! The shape is a flattened catenery - a more general family of curves which include the catenery. The equation (in its simplest form w/o translations) is y=a*cosh(b*x) and you would get a catenery only if b=1/a, which is only approximately, but for good reason not exactly the case with the Gateway Arch.
BTW, the approxomation equation (which forms a catenery) you gave uses the height information of 630 ft you can find in most folders. The real height of the arch centerline is "just" 625.0925 ft 😉 The half base length 299.2239 ft.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Sorry Valery, thats the Gateway Arch in St Louis, Missouri, U.S., not Australia (yes I know, you were thinking of upside down, down under, etc.).
Thanks, I know it - it is a picture from the Wikipedia article about Gateway Arch in St Louis.
Leopold, sorry, it was a joke about Australia people position - heads down - foots - up ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Sorry Valery, thats the Gateway Arch in St Louis, Missouri, U.S., not Australia
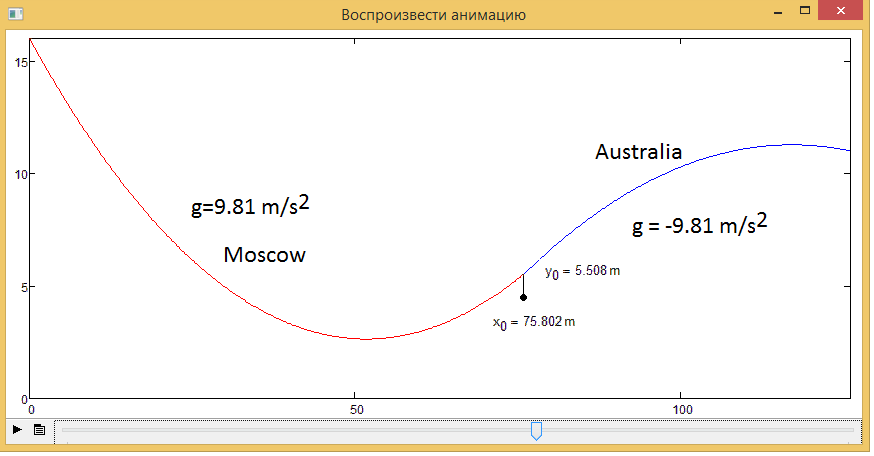
One more picture - one frame from "crazy canenary" animation:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
GREAT!! So thats the correct answer.
I didn't realize that the problem already was solved, but I could have bet that you would be the one finding the correct answer to your own question 🙂
Congratulation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now, thanks to Werner,I understand better what Valery was trying to do (famous last words!), I’ve come up with the following reasoning for his additional conditions.
We can assume the two parts of the chain are catenaries if they are, indeed, catenaries that have no added mass at a point. This can be made to represent the problem with an added mass at a point if the sum of the masses of the chains below the crossover point equals the added mass. In this case the parts of the chains above the crossover point don't "know" that they are supporting a mass rather than the rest of their own chain. This gives an additional condition.
However, the problem is incomplete until we specify what fraction of the added mass is supported by each chain. In the attached I allocate a fraction f of the added mass to chain 1. There are very sensitive limits to the range of acceptable values of f. In the attached a range of values of f between about 0.485 and 0.501 is all that seems to be acceptable! (But all of those in range are acceptable - i.e. there is no unique solution.) These values will be different for different values of added mass. There might be a logical way of reasoning about the acceptable range, but I just used trial and error. The image below shows the result with a 10kg added mass and a fifty-fifty split.
My advice: If you insist on adding masses at a point, stick to a discrete model!
This is definitely going to be my last post on this topic!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I played with Alan's sheet and came up with the following.
I'm still not convinced about the catenaries (see my other posts).
And I am absolute not sure about the distribution of the weight G on the two catenaries I made.
The solve block fails for some values of x0 and the results near the ends seem to be not that realistic.
What do you think?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
Half a problem.
Thanks Fred for the support!
"To be or not to be? That is the question!"
I think we can show it without DE - with a simple logic.
I see a part of chain:
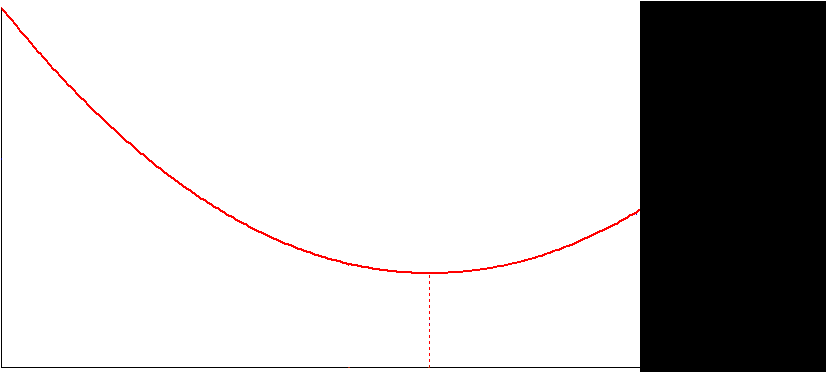
It may be so
or so (the load is fixed or very slow moves).
Or?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I think we can show it without DE - with a simple logic.
I see a part of chain:
OK. What is it we should see? I guess you mean we see an ordinary catenary, right?
It may be so
OK.
or so (the load is fixed or very slow moves).
No! Not OK. You already assume that a single point load generates a catenary to "show" that a single point load generates a catenary.
You can easily prove that the square root of 16 is 5 if you first assume that 5^2 is 16.
Thats TOO simple logic 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov wrote:
I think we can show it without DE - with a simple logic.
I see a part of chain:
OK. What is it we should see? I guess you mean we see an ordinary catenary, right?
It may be so
OK.
or so (the load is fixed or very slow moves).
No! Not OK.
Ooooooooooooooooo!
We have two fixed points and we can have between its only a catenary.
One (limit) form of a catenary is a straight line.
Our discussion here has a Russian name Толочь воду в ступе!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you are happy with your appraoch, fell free to stay with it.
As I had already written prior, evreybody is free to ignore arguments and hang on with his believe.
Valery Ochkov wrote:
One (limit) form of a catenary is a straight line.
Can you please show how by using the equation of a catanary and a mathematical limit rather than pics of brick walls?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The only way to convince Werner is with the pure physics; common sense be damned!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many good people in the past were victims of what they believed to be common sense ![]()
I'd be happy to be able to believe the solutions will be catenaries, so maybe you can explain how a linear function can be a special case of a catenary, that is, how the following limit would work? It seems to be beyond my mathematical and my common sense 😉

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Many good people in the past were victims of what they believed to be common sense
But in 99.9..% cases common sense = science!
I'd be happy to be able to believe the solutions will be catenaries, so maybe you can explain how a linear function can be a special case of a catenary,
Sorry, no a linear function a+b x, but I tell about a catenery like, near straight line!
I think this massage #100 is a dead point of this discussion. I would like to begin new one in new branch of this forum Or on one other Math forum. On one forum, where man does not say "I feel it is not correct, bu I do not know why!"

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think this massage #100 is a dead point of this discussion. I would like to begin new one in new branch of this forum Or on one other Math forum. On one forum, where man does not say "I feel it is not correct, bu I do not know why!"
Maybe its a good idea to post in a forum where no one is critically questioning your appraoch.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Werner, for the help an for the good idea.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Fred!
But one question to the second file - to last plot.
If I change x.o from 10m to others - 5m or 15m for example I see that H.2 on the plot is not equal 17m (the right end of the plot).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't get an automatic solution; the two files are two separate manual solutions. You need to alter the Horizontal tension and the weight share percentage to get the values of height and length to be correct. If you can figure out how to get the solve block to work (red Find()), then we've beaten this one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Let's begin with simple case.
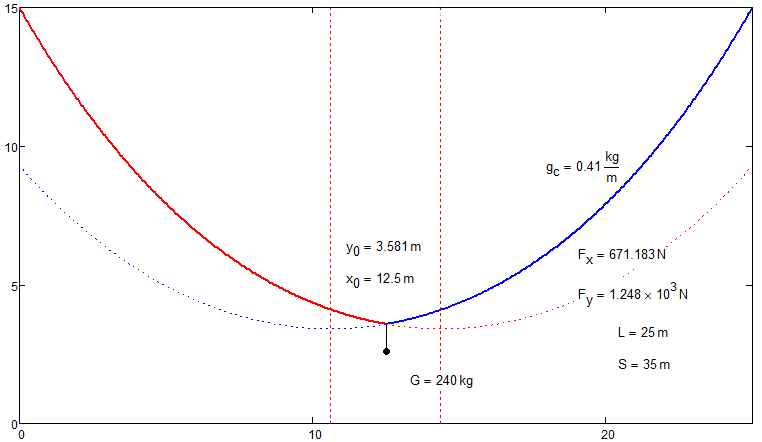
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The image looks like one of those that are labeled, "some features are exagerated for clarity."
I don't have any particular insight, but for a chain or cable that weighs about 5% of the suspended weight, I just can't see my way to a catenary with that much curvature. In fact, I would have expected for such a weight ratio that the chain would almost look like two straight lines.
TTFN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Arbiter 007 wrote:
The image looks like one of those that are labeled, "some features are exagerated for clarity."
I don't have any particular insight, but for a chain or cable that weighs about 5% of the suspended weight, I just can't see my way to a catenary with that much curvature. In fact, I would have expected for such a weight ratio that the chain would almost look like two straight lines.
Indeed it does!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Arbiter 007 wrote:
The image looks like one of those that are labeled, "some features are exagerated for clarity."
I don't have any particular insight, but for a chain or cable that weighs about 5% of the suspended weight, I just can't see my way to a catenary with that much curvature. In fact, I would have expected for such a weight ratio that the chain would almost look like two straight lines.
Indeed it does!
Alan
Yes, like two straight lines!
And what we have between:
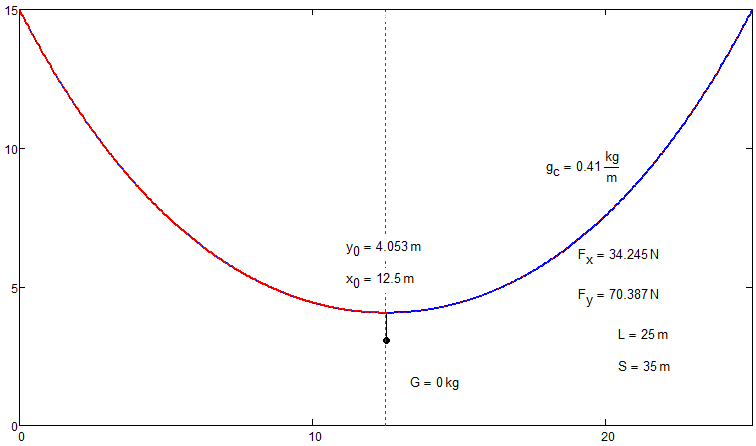
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I think I have one problrms with Given-Find block (CTOL, TOL, etc)
I don't know about TOL and CTOL Valery, but you certainly have a problem with units:
LHS is mass, RHS is force!
Also, this expression (even with corrected units) is only true if x0 is exactly half-way, which, in general, it isn't.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Valery Ochkov wrote:
I think I have one problrms with Given-Find block (CTOL, TOL, etc)
I don't know about TOL and CTOL Valery, but you certainly have a problem with units:
LHS is mass, RHS is force!
Also, this expression (even with corrected units) is only true if x0 is exactly half-way, which, in general, it isn't.
Alan
Thanks, Alan!
Better to solve this task in Prime with different dimension in the Solve block. But Prime has not animation.
See please http://communities.ptc.com/videos/4438
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
...
Better to solve this task in Prime with different dimension in the Solve block. But Prime has not animation.
See please http://communities.ptc.com/videos/4438
The units have been set to "none" in the MC15 version - why?. You could switch them on (to SI, say).
Alan