Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
One task - how can I use not rkfixed but odesolve?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One task - how can I use not rkfixed but odesolve?
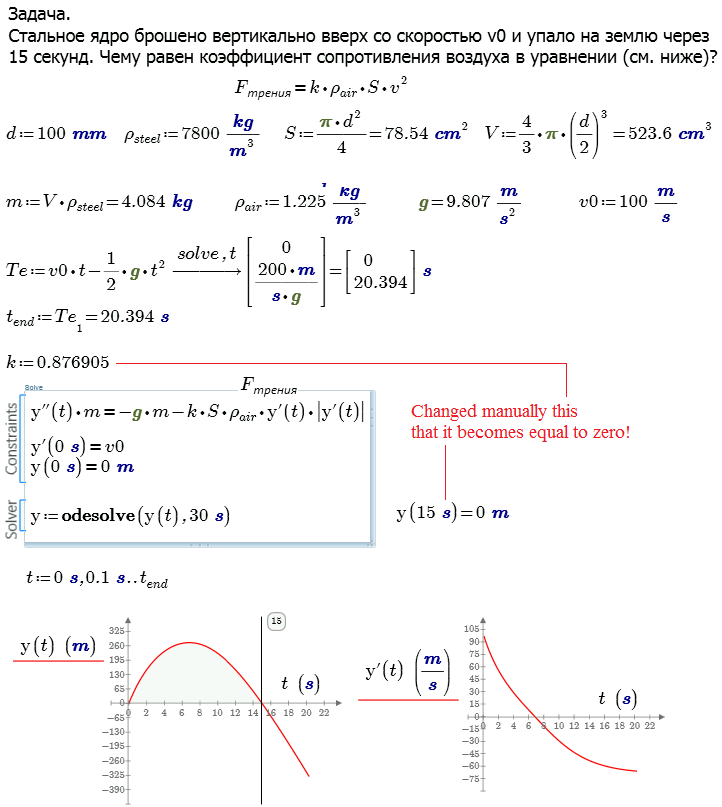
A Task.
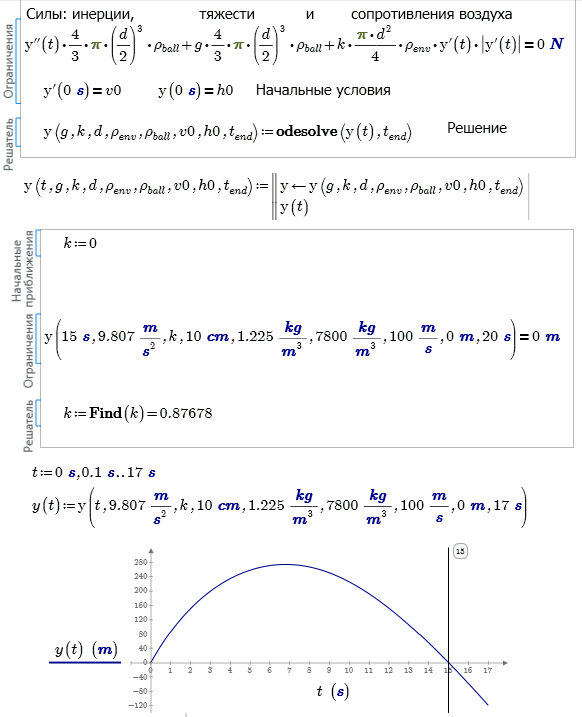
A steel core thrown vertically upward at a speed v0 and fell to the ground in 15 seconds. What is the coefficient of air resistance in the equation Ffriction = k S Ro v ^ 2? [The answer k=0.877 ![]() ]
]
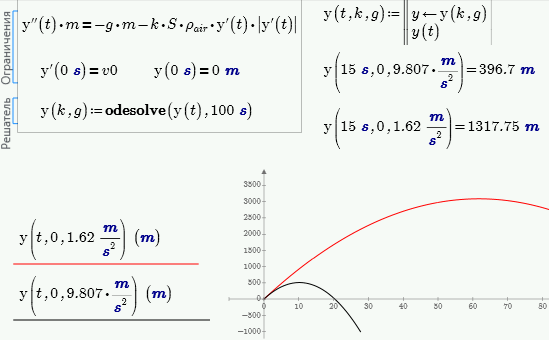
I have a solution with the using the rkfixed function (Mathcad Prime with UNITS!- see the attach). In Mathcad 15 we can not use units in this task ![]()
1. Is the solution correct?
2. How can I use not rkfixed but odesolve function?
3. I'll take the other comments and suggestions gratefully!

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Nearest I can manage.
Alan
Thanks for the idea.
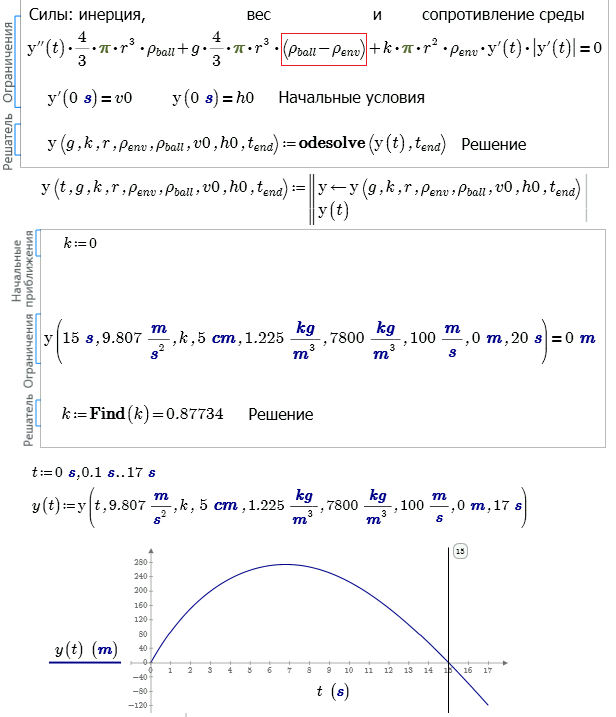
I think it is a solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A Westerman wrote:
Ode solved?
Problem may be redefinition of 'm'
Regards
Andy
Thanks!
But:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem may be redefinition of 'm'
No, not quite. Look at the Labels of y within Valery's Solve block. They are labelled "function" but should be labelled "variable". Also the "t" in "y(t)" in the argument within odesolve has label "none", but should have label "variable". I find this sort of thing occurs all too easily within Prime, making it still a toy not a real tool.
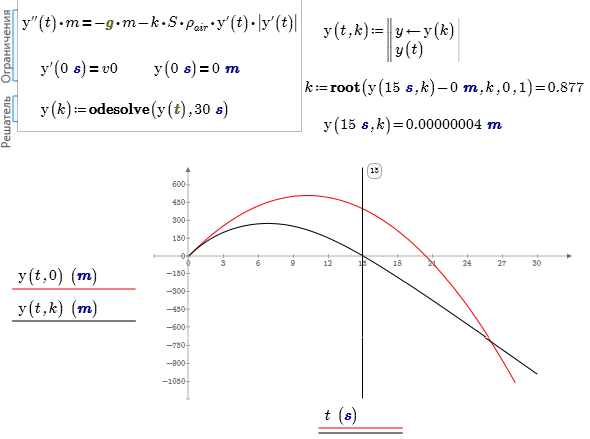
Meanwhile, the attached shows a way of solving Valery's original problem using odesolve.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Missed that the original had the issue of multiple uses of variable names - definitely a serious weakness in Prime.
But T15 (2) was re-written from 1st principles & lost that in translation.
regards
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A Westerman wrote:
Missed that the original had the issue of multiple uses of variable names - definitely a serious weakness in Prime.
But T15 (2) was re-written from 1st principles & lost that in translation.
regards
Andy
Yes, I often find problems in Prime can be fixed by rewriting from scratch!
Incidentally, Valery's problem can also be fixed by labelling all the y's and all the t's within his solve block as "none"!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just saw this thread. In Valery's original file, he used "m" both as a variable and as the unit "m".
He's able to do this with labels. The variable "m" has the label variable, and the unit "m" has the label "m", which you can see by the default blue color.
I'm logging the issue that Alan raised below with some of the labels showing the wrong color.
Mona
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mona Zeftel wrote:
I just saw this thread. In Valery's original file, he used "m" both as a variable and as the unit "m".
He's able to do this with labels. The variable "m" has the label variable, and the unit "m" has the label "m", which you can see by the default blue color.
I'm logging the issue that Alan raised below with some of the labels showing the wrong color.
Mona
Mona,
see please http://communities.ptc.com/message/190187
I think it is not correct (normal) with lables in the odesolve-block in Mathcad Prime and will be fine in Prime 3 or N.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mona Zeftel wrote:
I just saw this thread. In Valery's original file, he used "m" both as a variable and as the unit "m".
He's able to do this with labels. The variable "m" has the label variable, and the unit "m" has the label "m", which you can see by the default blue color.
I'm logging the issue that Alan raised below with some of the labels showing the wrong color.
Mona
Sorry Mona! But we say in same cases in Russia - you should at first "eat peas" before using the function odelolve with lables in Mathcad Prime ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Problem may be redefinition of 'm'
I find this sort of thing occurs all too easily within Prime, making it still a toy not a real tool.
Alan
I too!
Mona!
Do you read this?
And second.
I can create the function y(t, k) by the using the fkfiksed function but can not with the odesolve one![]() .
.
Somebody can?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
However we can use the odesolve! With grief in half! Pardon, with the bisection method!
See
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
However we can use the odesolve! With grief in half! Pardon, with the bisection method!
Did you see my file t15b above Valery? That uses the bisection method (automatically, not by hand).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Valery Ochkov wrote:
However we can use the odesolve! With grief in half! Pardon, with the bisection method!
Did you see my file t15b above Valery? That uses the bisection method (automatically, not by hand).
Alan
Thanks, Alan!
But it is very difficult!
I would like to have a function y(t,k) as in the sheet with rkfixed!
As in Mathcad Prime Minister - http://communities.ptc.com/docs/DOC-2999
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I would like to have a function y(t,k) as in the sheet with rkfixed!
I agree. It is frustrating not to have this capability.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Nearest I can manage.
Alan
Thanks for the idea.
I think it is a solution:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So Mathcad calculates faster, but we do not understand how to get this equation:
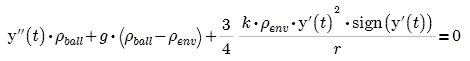
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Valery Ochkov wrote:
So Mathcad calculates faster, but we do not understand how to get this equation:
Haven't you got a y'(t) too many here Valery? i.e. shouldn't y'(t)^2.sign(y'(t)) be just y'(t).sign(y'(t))?
Alan
Sorry I do not understand your question!
y'^2.sign(y') is equal y'*|y'| - the vector of the friction force is opposite the vector of velosity!
But what is fester?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oops! I read sign(y'(t)) as absolute value of y'(t)!
But I don't understand what you are asking. Is what faster than what?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
But I don't understand what you are asking. Is what faster than what?
Alan
What is fester? y'^2 * sign(y') or y' * |y'| ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator