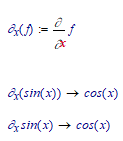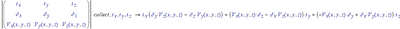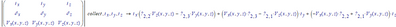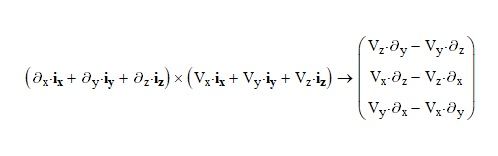- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Partial derivatives operator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Partial derivatives operator
Hi,
How can I modify the operator so that it works correctly and not as shown in the figure? In the image what I would like is marked in red:
I used a letter linked to the sword symbol (but I could have used others) because when it is used as an argument of a function in a reference file, it is sure that, in the calling program (s) (in which I will be careful not to use that symbol, linked to the sword symbol), no conflicts arise.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would need something more than previously said. For example, use those operators in the rotor calculation as in the figure:
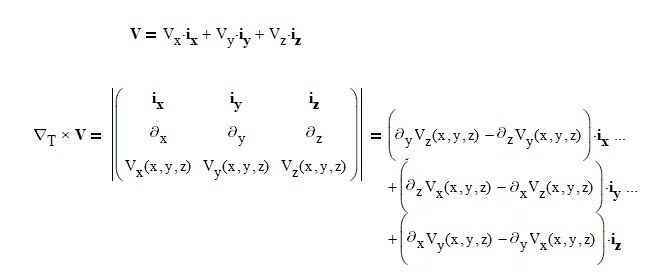
is it possible?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm afraid not. And I doubt if the operation, defined through the determinant, is mathematically correct.
Anyway, if all items of the 3x3 matrix are just symbols, this is what you get:
So it looks great, until you look closer. In the first term of i.x, the partial derivative to y is not applied to V.z, but simply multiplied with it.
With the partial derivative 'operators' (in fact they're defined as functions) defined you're getting undefined items.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
in fact that is a mnemonic rule for calculating the rotor. It is also given by the vector product between the vector of the operators and the given vector.
which also makes no sense.
Obviously, your displayed result does not make sense as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Are you aware that the del symbol is the functional gradient operator? In Mathcad 15 (not Prime) you get it with cntrl+shift+G, you can subscript which variables you want to take the derivative of. There were a few old posts . ..