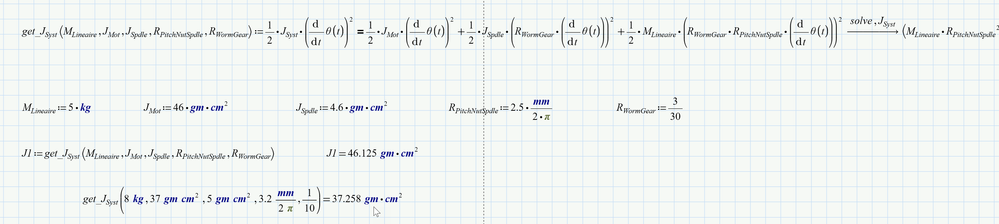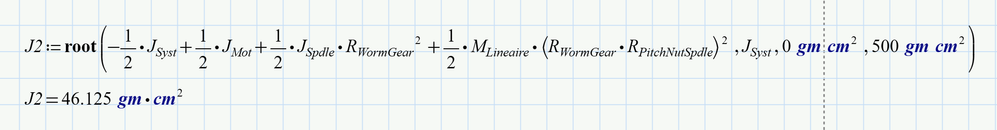We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Pb to allocate a result from symblic Solve to a variable
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Pb to allocate a result from symblic Solve to a variable
Hello
I am want to use Mathcad to build a mathematical model from several physical formulas and later on substitute either numerical values either lower formulas.
The 1st difficulty I meet is that I would expect hereafter to get numericla result in the variable JSyst. Currently the error is "undefined variable".
Another strange thing is the numerical resuls from the Solve command is not combining the unit.
Is there a common explanation ?

Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
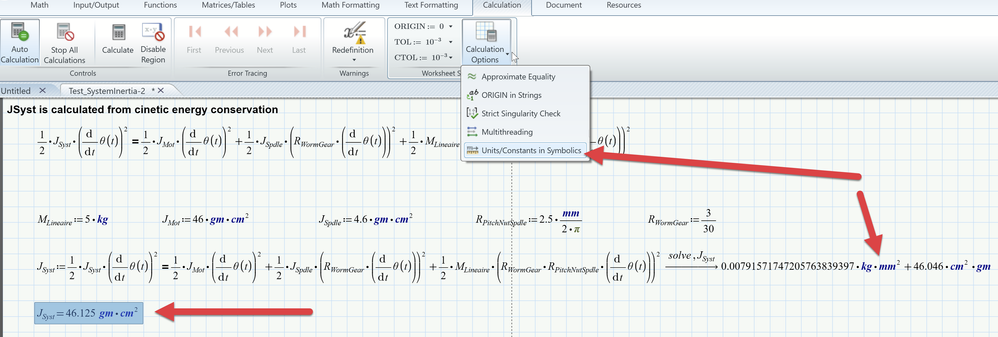
You have to know that the symbolics does not understand anything about units. It does not know that 1cm=10mm or the like. So it treats each unit as an unknown variable and therefore can't simplify them.
Checking "Units/Constants in symbolics" is a good idea and you should do it. The symbolics still don't know anything about units, but at least Prime labels these units in the symbolic result as being a unit (you can see that kg, mm, etc. is now shown in bold and blue) and therefore the native numeric engine in Prime can numerically evaluate the variable and of course it simplifies the units as well:
I would suggest other approaches:
1) You may turn the symbolic solve result into a function of the involved variables. That way you could easily compare evaluation with different input values side by side.
2) If you are only interested in a numerical result, you may consider to avoid the symbolics altogether a use one of Primes numeric methods for solving an equation. You have the choice between a solve block with "find" or using the "root" function. The root function could be used in two flavors - either by providing a guess value or by providing an appropriate lower and upper limit for the variable you want to solve for.
Here is the last mentioned method - root-function and providing a range from 0 gm cm^2 to 500 gm cm^2.
I had to get rid of the derivative of theta(t) which cancels anyway and also had to get all expressions to one side of the equation because "root" will not solve equations but rather looks for the zero of a function:
Prime 9 worksheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
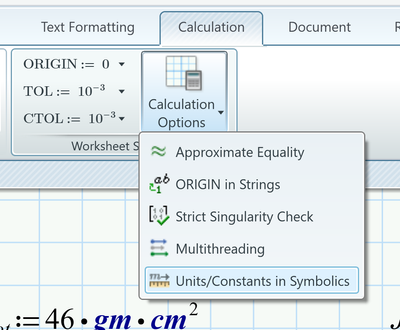
Easy solution here. On the Calculation tab/Calculation options, turn on Units/Constants in Symbolics.
Bob
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your prompt answer.
But this does change anything.
1- I wonder if the units are well recognized.
2- Still JSyst appears undefined ???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The "Units in constants/symbols" works sometimes, that is, not always.
If you want to use symbolics, then work symbolically only.
If you want to get numerical data using symbolical definitions, make them as functions. So define
J.Syst(J.Mot, J.Spdle, ....) :=
Then you can call it with the numerical data.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry about that. I should have said to recalculate the document after making the change. When I did that on your document, JSyst was defined.
Bob
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have to know that the symbolics does not understand anything about units. It does not know that 1cm=10mm or the like. So it treats each unit as an unknown variable and therefore can't simplify them.
Checking "Units/Constants in symbolics" is a good idea and you should do it. The symbolics still don't know anything about units, but at least Prime labels these units in the symbolic result as being a unit (you can see that kg, mm, etc. is now shown in bold and blue) and therefore the native numeric engine in Prime can numerically evaluate the variable and of course it simplifies the units as well:
I would suggest other approaches:
1) You may turn the symbolic solve result into a function of the involved variables. That way you could easily compare evaluation with different input values side by side.
2) If you are only interested in a numerical result, you may consider to avoid the symbolics altogether a use one of Primes numeric methods for solving an equation. You have the choice between a solve block with "find" or using the "root" function. The root function could be used in two flavors - either by providing a guess value or by providing an appropriate lower and upper limit for the variable you want to solve for.
Here is the last mentioned method - root-function and providing a range from 0 gm cm^2 to 500 gm cm^2.
I had to get rid of the derivative of theta(t) which cancels anyway and also had to get all expressions to one side of the equation because "root" will not solve equations but rather looks for the zero of a function:
Prime 9 worksheet attached