Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Performance Issues
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Performance Issues
Hi,
I am having performance issues with the attached worksheet and would appreciate any help/guidence. I am trying to calculate the deflection and stress along a pipeline during flooding / installation. I am relatively confident that the equations are correct, as the spreadsheet works for a single input of water depth (delta c).
So the aim of this sheet is to rewrite it so that maximum water depth is calculated based on allowable stresses. I have managed to calculate the deflection, slope and bending moment, but the spreadsheet takes a long time to converge. I am looking for a more efficient way as I have passed delta c to all dependent variables and sure this is the issue. .
Thanks in advance.
Mike
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Mike, long time no see.
You call the solve block function "Func" really very, very often in your various routines. Better call it just once (or at least only once per plotted point) and pass the result as additional argument.
See if the attached can be of any help.
On a slow machine here the plotting of the slope diagram speeds up from 52 seconds to just 6 seconds.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Instead of the first solve block, you could have used:
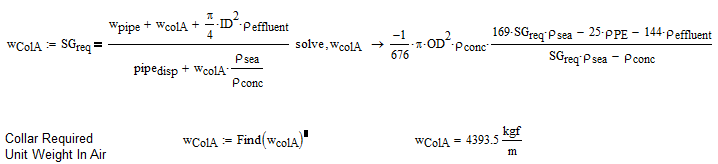
(I've undefined all your parameters first:  , etc) and it did not improve the speed
, etc) and it did not improve the speed ![]() .
.
Unfortunately for the second solve block I haven't found a way to solve it symbolically....
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for looking at it Luc. I think Werner has solved it.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Mike, long time no see.
You call the solve block function "Func" really very, very often in your various routines. Better call it just once (or at least only once per plotted point) and pass the result as additional argument.
See if the attached can be of any help.
On a slow machine here the plotting of the slope diagram speeds up from 52 seconds to just 6 seconds.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Werner, excellent effort as always.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
I am having further performance issues when I try to differentiate slope to calculate the bending moment, and subsequently calculate the stress.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
M is the first derivative of theta (I*E is just a constant factor) which is the first derivative of y. All derivatives are evaluated numerically.
That means, the every single call to M has to calculate the derivative of y again and again.
Using the second derivative of y directly reduces calculation time from 98 seconds down to 6 seconds:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Another good point.
I made the following change so omega b and delta b did not call func throughout the worksheet, which reduced the time to zero:
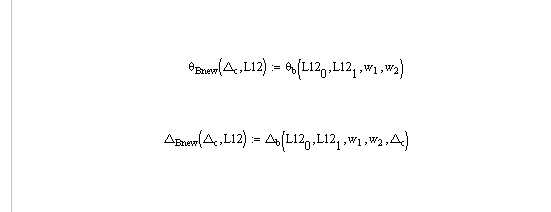

Thanks,
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah! I see. I had overlooked theta.B and Delta.B when I changed the functions in my first answer.
Now its really pretty fast.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cheers for the help.





