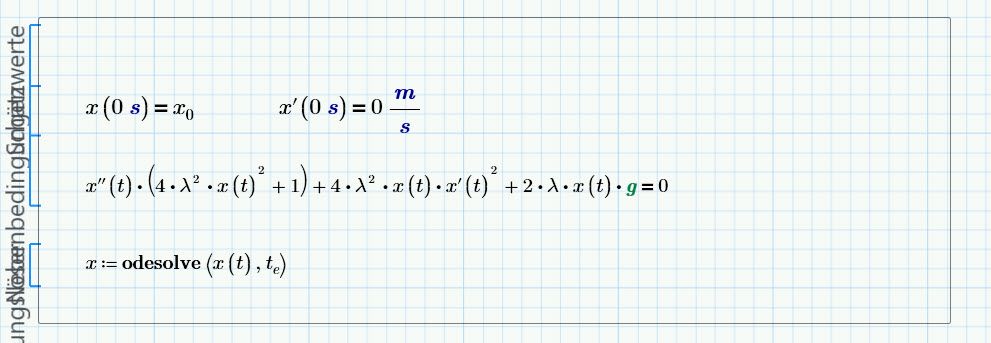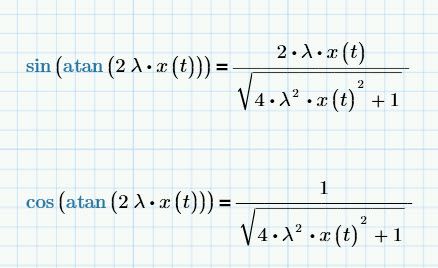Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Point-Mass at it's Orbit: Newton's Equations searched
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Point-Mass at it's Orbit: Newton's Equations searched
Hello!
I have calculated the complete dynamics for a mass-point moving along a parabola curvation without any resistance like air-resistance, friction, etc.
The solution is correctly solved with the Lagrangesche-methos, the movement happens in that way i suggested.
But sometimes it's very complex to create ODEs in that way and therefore it's better to use Newton's Laws.
I tryed to solve the problem with the dynamic balance of forces acting on the mass, but i couldn’t get the same solution in that way so i’m asking what’s wrong. (please see attachement including MP4 and Pdf-file)
Can somebody tell me what’s wrong there?
Thank you very much.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
In principal i understand what you calculated.
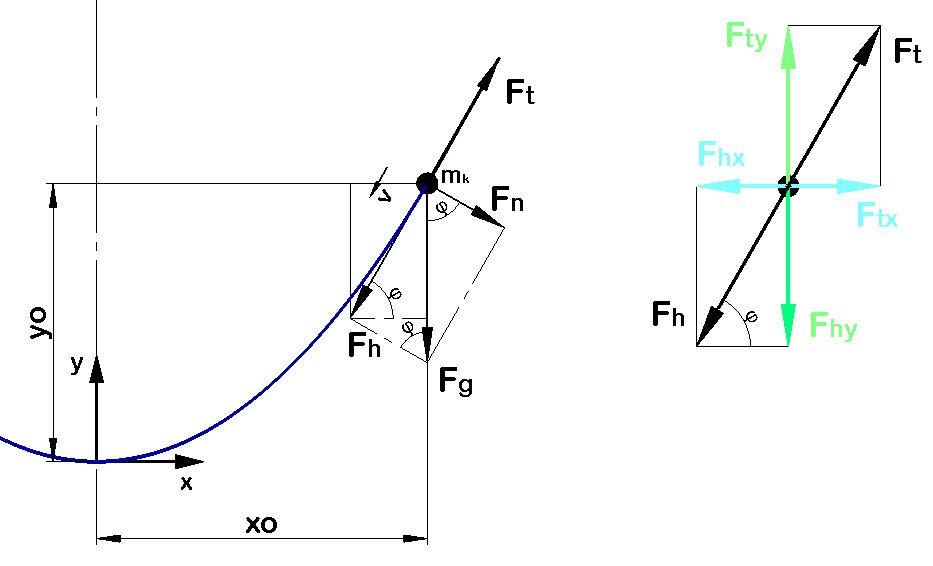
But what i do not understand is: The sign of the force Fhx.
Initial situation:
The body is on the right side and we release it at xo, then it moves along downwards the curvature to the left.
I calculated Fhx as negative and added Ftx, this should be zero.(see sketch)
Fhx (yellow) is acting from right to the left side and will accelerate the body, the force Ftx acts from left to the right because the body has the intension to stay at the position he is (=Trägheitskraft).
If i built the sum, then i have: -Fhx+Ftx=0 what gives a wrong graph, but the dynamic statik says: the sum of all forces have to be zero. In many textbooks i saw this same procedure.
When changing the sign of Fhx to positive, i get a correct graph like you have.
Now i'm confused because i know that the sum of all acting forces have to be zero taking into account their direction they act.
I had the same problem in the thread: https://community.ptc.com/t5/PTC-Mathcad-Questions/Hello-World-See-my-1-st-Prime-Animation/td-p/196317/page/7
neither something in my interpretation is basically wrong, nor something other don't work correctly.
Please explain me.
Thanks for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Another example for the sum of all forces:
We have an inclined plane without friction and any resistance, then it is (like in many textbooks):
This princip is the same with the parabola.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The disconnect is the "sum of forces equals zero." If the forces sum to zero there will be no acceleration (F = ma).
So there must be a force unbalance.
I tried to solve for acceleration along the curve, using the tangential component of weight; but I'm not good enough to sort x and y out of the acceleration along the curve.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
it's easy for the acceleration along the curve.
You can use the solved x(t) to compute this acceleration and make a new balance of forces with m*a=-Fh:
Anyway: I'm not familiar with the Signs of the forces in the balances. We have a dynamic statik.
See attachement please.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"
The disconnect is the "sum of forces equals zero." If the forces sum to zero there will be no acceleration (F = ma).
So there must be a force unbalance. "
An what is now about this:
There is a contradiction!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Something else has occurred to me:
comparing the ODE from the Lagrangesche Method with the ODE from the Newtons method shows following:
Lagrangesche ODE:
Newton's ODE:
Note, that the sin and cos functions can be written here as:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All this is from my textbook kinetics, technical mechanik 3:
The origin task see example 4.5 in this textbook.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Volker,
Could you be interested in the following Lagrange multiplier technique?
Greetings
Francesco
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Francesco,
Absolutely!
It's impressive.
could you attach this file please- then i can study it much better.
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Volker,
I've attached the requested file.
I hope I've zipped the file correctly.
Greetings
Francesco