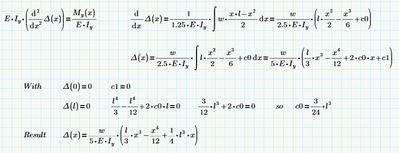Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Prime 7 and odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 7 and odesolve
I recently encountered an issue with Prime 7. The function odesolve doesn't work the way it used to in Prime 5 and I can't figure out why.
I'm updating my MathCAD sheets to Prime 7 and my current header and coding standards, and finding that there's an issue with odesolve.
Here is my solve block showing the differential equation for deflection of a beam. It's a simply supported beam, so deflection delta at 0 and at the beam's end L are both zero.
E is in units of GPa, Iy in units of mm^4, length l in units of m, and M(x) in units of kN*m. I have verified that all units are correct.
When I open this MathCAD sheet in Prime 7, I get an error "These units are not compatible", but when I open it in Prime 5, I get no error and the thing works.
What is different about Prime 7 that causes the functionality not to work anymore? MathCAD sheet attached.
Please help!
Thanks!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK... I don't know why this is, but I solved my problem. You're not gonna believe the solution.
In the boundary condition at d(l) = 0 in, I had to delete the units from the right hand side of the equation.
I don't know why, and it definitely shouldn't work this way, but it works.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK... I don't know why this is, but I solved my problem. You're not gonna believe the solution.
In the boundary condition at d(l) = 0 in, I had to delete the units from the right hand side of the equation.
I don't know why, and it definitely shouldn't work this way, but it works.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Glad you found the problem.
You could directly calculate the maximum deflections.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Terry. The reason I do it using odesolve and not the direct formula is because I sometimes need to change the M(x) equation. It's easier and I make fewer mistakes to only change one thing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Some calculus. if I made no mistake, gives:
You should be able to compare that with the Odesolve result.
(I'll leave the other ODE to you...)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
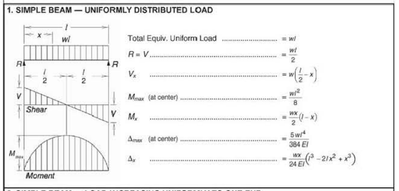
Hi Luc,
Your answer is really close to the formula published at
Digital Edition - 14th Edition Steel Construction Manual (usc.edu)
Well done with your calculus!