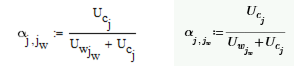Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Prime 7 swapping row and column order from Mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 7 swapping row and column order from Mathcad 15
Hi, I've recently been tasked with updating some Mathcad sheets from version 15 to Prime 7 and have noticed something that has confused me. (Unfortunately as they aren't my sheets and I'm only upgrading them I don't have full permission to upload the mathcad files but I can send some screenshots, but anyways)
Using the following equation, on dropping the subscript [ j, jw after the α, they both give the same identical matrix.
However, when reintroducing the [ j, jw subscript (sorry I don't know the proper term, again I'm just converting the files - the maths itself is beyond me), the output in Mathcad 15 is different from Prime 7.
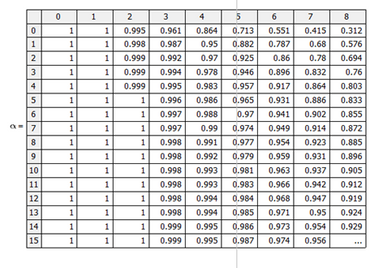
In Prime 7, it creates a vector starting from the first row of α, and then from the second and then third row etc.
However, for 15, it creates a vector starting from the first column of α, and then the second and the third etc.
Is this something that was changed in the update that I'm not aware of, is there a setting in either of the Mathcad versions which might have been changed that is causing this discrepancy, or is it something else entirely?
Thanks in advance.
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
-
Mechanical_Engineering
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Figured it out.
The expression α[j,jw=, with j and jw range variables that span the rows and columns respectively, results in the serialization of the matrix α.
Example:
Prime does it row by row, Mathcad does it column by column:
So yes, there is a difference in behaviour between Mathcad and Prime. (And this is not the only example of that...)
To get the same result in Prime, you could use the transpose operator, but you also need to swap the indices then.:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is the matrix α the same size in both cases (Mathcad & Prime)?
In Prime it appears to have 20 rows and 32 columns.
You can check sizes with:
rows(α)=
cols(α)=
If so, then how do you get indices above 31 in the Mathcad output?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Figured it out.
The expression α[j,jw=, with j and jw range variables that span the rows and columns respectively, results in the serialization of the matrix α.
Example:
Prime does it row by row, Mathcad does it column by column:
So yes, there is a difference in behaviour between Mathcad and Prime. (And this is not the only example of that...)
To get the same result in Prime, you could use the transpose operator, but you also need to swap the indices then.:
Success!
Luc