Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problem solving system of ODE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem solving system of ODE
Hello everyone, i hope all are having a great day.
I started this discussion because im having a little problem solving a system of 2 ordinary diff eqs.
Im not defining a function for t or x because theres not a way to put this in function of w.Also I dont know if i define w with a random numer and t and x with random functions would affect the final result. I just want to solve the differential eqs. I defined r(w) for example for simplicity.
The problem im trying to solve is for chemical engineering. Its about solving the mass and heat differnetial eq simultaneously. Heres the document.
Thanks for your time
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is one possible solution. Other approaches would either copy the expressions of your function Ca, k and r directly in the solveblock equations or include those functions in the solve block (using the boolean 😃 and solve for all five functions.
BTW, the last (optional) argument of odesolve() is the number of iteration steps (not the step width) and has to be a positive integer (default is 1000).
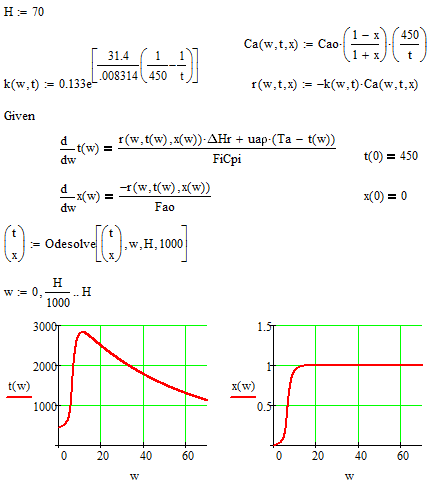
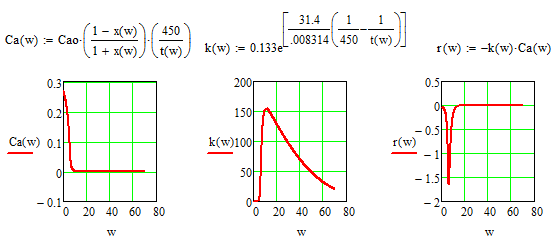
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is one possible solution. Other approaches would either copy the expressions of your function Ca, k and r directly in the solveblock equations or include those functions in the solve block (using the boolean 😃 and solve for all five functions.
BTW, the last (optional) argument of odesolve() is the number of iteration steps (not the step width) and has to be a positive integer (default is 1000).


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
Is there a reason you inverted the RHS of the second ODE? Alexander had Fao/-r.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
Werner,
Is there a reason you inverted the RHS of the second ODE? Alexander had Fao/-r.
??? As far as I see I haven't changed anything.
This is what I see when I open his original sheet:

BTW, attached is a second approach using five functions to solve for.
EDIT: Just noticed that in my first file those three functions (r,Ca and k) won't need w as argument. It doesn't hurt but its obsolete.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner, thanks for posting both of the possible ways to solve this problem. Now I understand a little bit more how to use correct notation. Thanks for taking your time to reply and correct my worksheet. Hope you have a nice day!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello again Werner, I have a doubt , wonder if you can help me. I know H is the limit of integration, if i put x(60)=0.922, but lets imagine this case that H=10^15, the value of x(60)=7.608x10^-6. Why does this happens? It should remain constant but it doesnt.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alexander Alvarez wrote:
Hello again Werner, I have a doubt , wonder if you can help me. I know H is the limit of integration, if i put x(60)=0.922, but lets imagine this case that H=10^15, the value of x(60)=7.608x10^-6. Why does this happens? It should remain constant but it doesnt.
In a perfect world with a perfect solution, that is an exact, symbolic solution - yes, you would get what you expect.
But you have to understand that Odesolve uses a numerical iteration algorithm, an approximation. In fact you can chose among a couple of algorithms if you right click the word odesolve.
The farther you get away from the starting point (0), the more inaccurate the results will be. Also the number of intervals chosen is of importance. Default is 1000 and I added this as the last argument of Odesolve. You set the end value of the interval to 10^15? Politely spoken thats not a good idea. You get a solution consisting of just 1001 points and inbetween Mathcad would simply interpolate. So the first point will be at 0, the next at 10^13, then 2*10^13, etc. You really can't expect a meaningful value at x(60)!
You can go up to H:=10^7 - if you set the number of intervals to 10^6 you still will get the result you expected for x(60). Going even more up with the number of intervals may be possible, but it sure will take a very long time to calculate and eventually you will run into memory problems.
So, no! You can't extend the integration interval to "infinity" and honestly - why would you do so??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks a lot Werner, it was just curiousity. Thanks a lot really for your help
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As Alexander sent me a private message asking me to look at his file I've attached my response here, though I see Fred and Werner have already tackled it.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Alan, thanks for taking your time to reply my message. It was really helpful those notes you put in the worksheet. As you can see im starting to learn on how to use this progam. Thanks a lot, I hope you have an awesome day!





