- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problem with units and odesolve using Mathcad Prime 1.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem with units and odesolve using Mathcad Prime 1.0
As recommended by Valery in the previous discussion, I have tried to set up units in a first order heat transfer ODE but am having difficulty with that task. As you can see this I have used various workarounds - first defining the units then stripping the units from variables etc in order to plot the intermediate results. The main problem however, is with the units in the ODE solve block. What I don't understand is why although all units have been explicitly defined in a table at the beginning of the worksheet, nevertheless the ODE reports that the "units are not compatible"? I have tried to explicitly insert the units into the solve block however nothing seems to work. As you can seen from the previous discussion I know this ODE works if you don't have units but I thought one of the big advantages of MathCad Prime 1 was that it can use units in solve blocks. Am I correct in that assertion and if so can someone work out why this error is resulting.
Thanking you in advance.
Kind regards, Mark Buckton
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark,
I am not really use to Prime yet, so I might miss something, but:
You stripped the units from Ts before the solve block, and Tf has units if K, that is one problem.
Also t is defined as a range variable, to the functions are defined at points only. I did not see an equation for Ts, but it seems you can use that way with range variables; but I don't think that is what you want. Try using t' or tt for range variables for plotting and t for the variable otherwise.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wayne;
Thank you for your suggestion I have tried what you suggested but to no avail.
Regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark!
Thanks for use my tip!
I think you must use units in Cs function too!
See the picture in attach!
PS
I have a dream to rewrite this book for Mathcad Prime with units in ODE
http://www.springer.com/engineering/computational+intelligence+and+complexity/book/978-3-642-05878-3
but when I have got Mathcad Prime 7.0 ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery;
Thanks for the tip; as you can see it is better but still the ODE refuses to reveal the function for T.s i.e. the steel temperature at a given time due to heat transfer.
What else am I missing i.e. why are the units incompatible with the ODE solver?
Regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See the picture and try please convert to order the right part of the ODE:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery;
I know you are trying to make me think through the problem to a solution but the recent tip you have provided is too obtuse for me to follow. Would you have the time to alter the my worksheet to show the solution? I rarely have success with MathCad units because most of the stuff I play around with is empirical formulas and thus units don't balance but in this case units should work because the formular is derived from theory and especially since the non unit version has been shown to provide a solution but where am I going wrong?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Buckton wrote:
I play around with is empirical formulas
Empirical formulas work fine with units! Imust only insert units in this formulas how I have shown it you and show again now in the picture.
And second.
Before to solve an ODE it would be good to check the right part - see thre picture:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery;
I have rechecked the equation by reference to the original literature in which it was derived and all looks OK. I have also checked the units as recommended but I think there are still problems. Obviously the solution of the differential equation T.s must have units of temperature (representing the steels temperature) in this case Kelvin i.e. K but I cannot get this unit out of the equation. Can you see where I am going wrong? Please refer to the attached worksheet.
Regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think better is so - see the picture in attch (Ci is unitless)!
We can see in this EMPIRICAL function an unit of argument and unit of function.
PS
We can see in reference books 3 types of formulas:
- physical formulas (connected physical quantities)
- empirical formulas (connected units of physical quantities)
- pseudoempirical formulas. Do you know what is it!?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm willing to forgive many developers of Mathcad Prime only for that they are trying to introduce the dimension/units in differential equations... This problem is not solved in Maple yet... But in Mathcad Prime...
Mona, do you hear me!?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan and Valery,
Thank you very much for your advice and forbearance, this is just what I wanted. I forgot the fact that this heat transfer formula is applicable to per lineal meter of beam. The main thing however is that I learnt something i.e. how to put units into ODEs and also how one attaches then to programming blocks - fantastic!
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See the same task - the density of water as function of temperature at p=1atm
On-line calculation on Mathcad Server:
http://twt.mpei.ac.ru/MCS/Worksheets/WSP/LiquidWaterDensity.xmcd
and the screenshot:
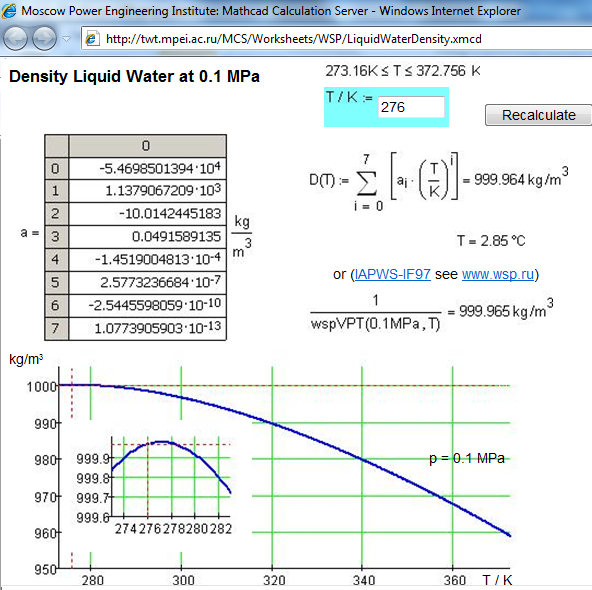
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan;
I spoke too soon.
If this is how the ODE solver works with units then I suspect there is something seriously wrong with the MathCad's ODE algorithm? Compare your unit version setup with the previous one done with no units. Note the solution plot of the ODE solution with no units is what would be expected i.e. the steel temperature should slightly lag the fire temperature noting that in this case this should be so as we are modeling the heat transfer to a light weight steel section. What we see in the ODE which uses units, however is the incorrect shape to the steel temperature rise i.e. concave up. I have plotted this together with the fire temperature curve and as you can see, and in humble opinion, the lag between these 2 curves is much too great.
Kind regards, Mark
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Buckton wrote:
Alan;
I spoke too soon.
If this is how the ODE solver works with units then I suspect there is something seriously wrong with the MathCad's ODE algorithm? Compare your unit version setup with the previous one done with no units. Note the solution plot of the ODE solution with no units is what would be expected i.e. the steel temperature should slightly lag the fire temperature noting that in this case this should be so as we are modeling the heat transfer to a light weight steel section. What we see in the ODE which uses units, however is the incorrect shape to the steel temperature rise i.e. concave up. I have plotted this together with the fire temperature curve and as you can see, and in humble opinion, the lag between these 2 curves is much too great.
Kind regards, Mark
My fault! I assumed your cp function returned values which are kJ/(kg.K). If this is changed to J/(kg.K) you get the same comparison graph of temperatures at the end as in the unitless version.
Alan
PS Assumptions should be made in the following order:
1st: The user is wrong.
2nd: The programmer is wrong.
3rd: The algorithm is wrong.
The computer, of course, is never wrong!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan;
Thank you very much. Well it seems I was too quick in jumping to the 3rd conclusion.
Kind regards, Mark





