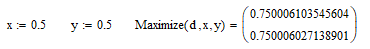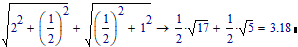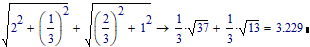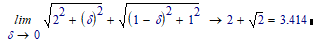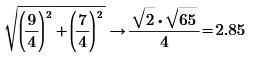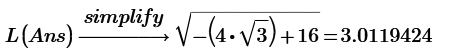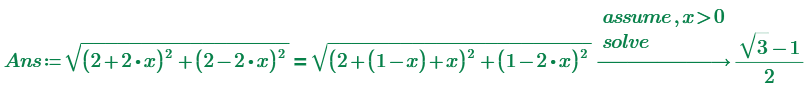Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Puzzle 28 Find the most far point from [0 0 0].
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Puzzle 28 Find the most far point from [0 0 0].
Make 1 ohm by 1 ohms is my best electric circuit puzzles.
I show the 1D, 2D and 3D lattice answers. Maybe these are the only one solution for each dimension.
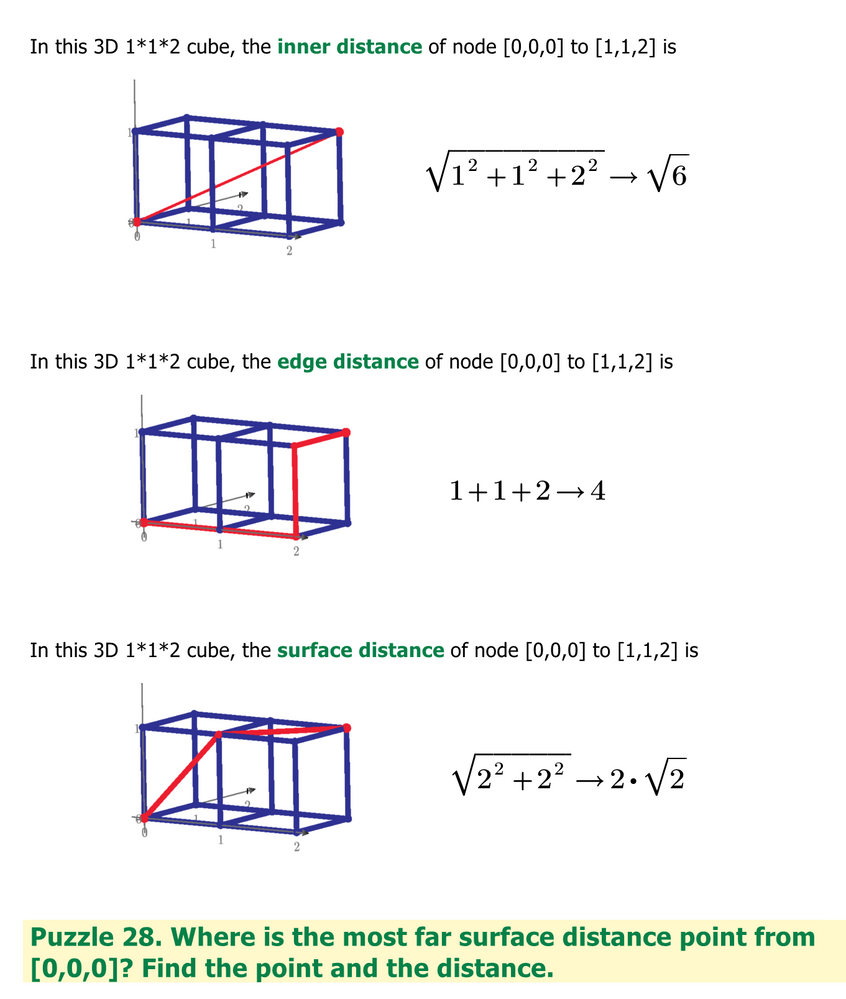
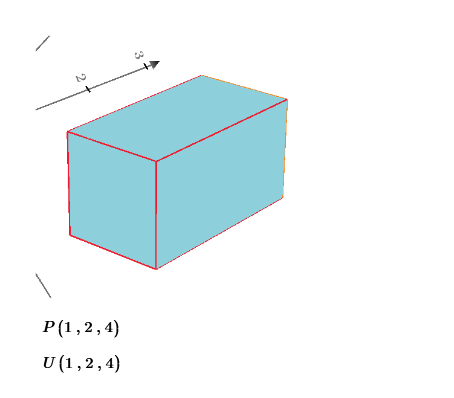
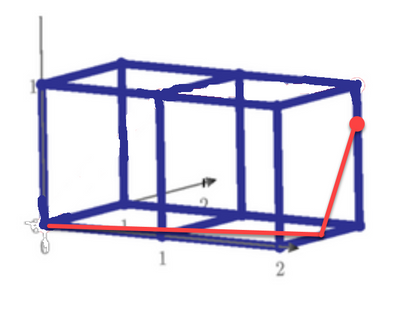
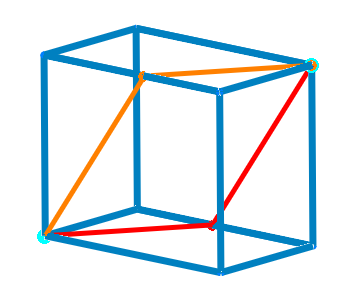
Puzzle 28 is using this 3D lattice shape 1*1*2. Where is the most far surface distance point from [0,0,0]?
Find the point and the distance.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
For the 3*4*5 cube, the surface distance of [0,0,0]-[3,4,5] is.
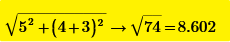
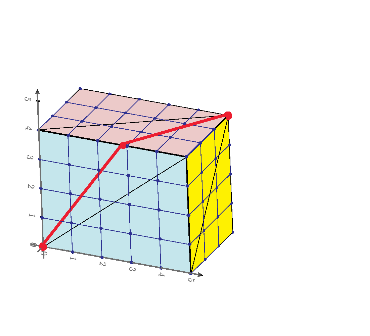
Yes, but.... I thought the task is to find the point with the largest surface distance from (0;0;0) in a 1 x 1 x 2 cuboid.
And I would say that (0.75; 0.75; 2) would be a good candidate:
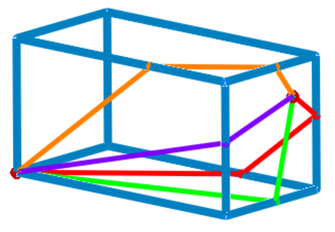
There are four possible ways from (0;0;0) to (0.75; 0.75; 2), all the same length!
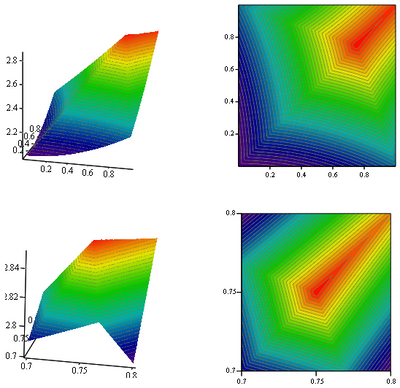
But I am missing a true proof that its really the point with the largest distance. I just have a numerical
and an optical confirmation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The 3D object you show consists of line segments only. You will have to define what exactly you would like to call a "surface" and how exactly you would like to define "surface distance" of two "points". I assume that with "points" you only mean the endpoints of the line segments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In this puzzle, surface means the surface on the 1*1*2 cube as shown below in blue color.
Point means any point on the surface and not only the integer nodes.
Distance means the shortest way by connecting two points by string on the surface.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That could be any point on the block, depending how many times you want to go around.
Limiting myself to go from 0,0,0 to 1,1,2, I could also go from 0,0,0 to 0,1/2,2, and from there to 1,1,2, then the 'surface distance is:
or go from 0,0,0 to 0,1/3,2 and then on to 1,1,2, which gives:
better still, choose any fraction delta and go via 0,delta,2 to 1,1,2 gives at maximum:
all of which is more than
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. Sorry my explanation is poor.
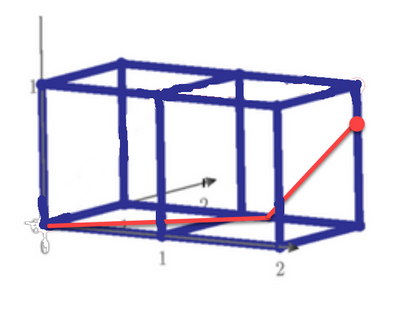
Start point is fixed to [0,0,0]. End point is not fixed to [1,1,2] but any point on the surface. So, find the most far point on the surface from [0,0,0].
The surface distance from [0,0,0] to [1,1,2] is "the shortest way" on the surface and it is 2*sqrt(2).
(The surface distance from [0,0,0] to [1,1,1] is "the shortest way" on the surface and it is sqrt(5).)
Tokoro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So the surface distance from (0;0;0) to (1;0.8;2) is 1/5*sqrt(221)=2.973... ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. Using Deployment Diagram, your case is
Therefore, the surface distance from [0,0,0] to Point [1,0.8,2] is shorter than 2*sqrt(2).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, you are of course right!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
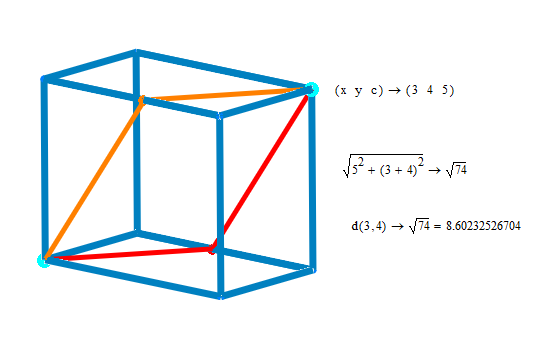
For the 3*4*5 cube, the surface distance of [0,0,0]-[3,4,5] is.
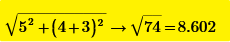
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
For the 3*4*5 cube, the surface distance of [0,0,0]-[3,4,5] is.
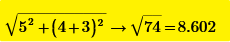
Yes, but.... I thought the task is to find the point with the largest surface distance from (0;0;0) in a 1 x 1 x 2 cuboid.
And I would say that (0.75; 0.75; 2) would be a good candidate:
There are four possible ways from (0;0;0) to (0.75; 0.75; 2), all the same length!
But I am missing a true proof that its really the point with the largest distance. I just have a numerical
and an optical confirmation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Then, the last question is what is the largest surface distance on a 1 x 1 x 2 cuboid?
It means we need two points on the surface and the distance is larger than above result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, I don't see a proof in your picture. Actually I am nor sure what you ar showing at all.
It looks like you are already assuming that for the solution it must be x=y. Why?
Then in your "deployment diagram" yo seem to consider only two ways a distance could be measured, but actually there are four.
You also seem to assume that for the largest distance these two paths have to be of equal length. While that is true (I had shown that even four different paths are of equal, maximal length) I wonder what justifies to assume that from the very beginning.
And then I don't see the meaning of your x:=2 y:=3 z=0 and Z:=3
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
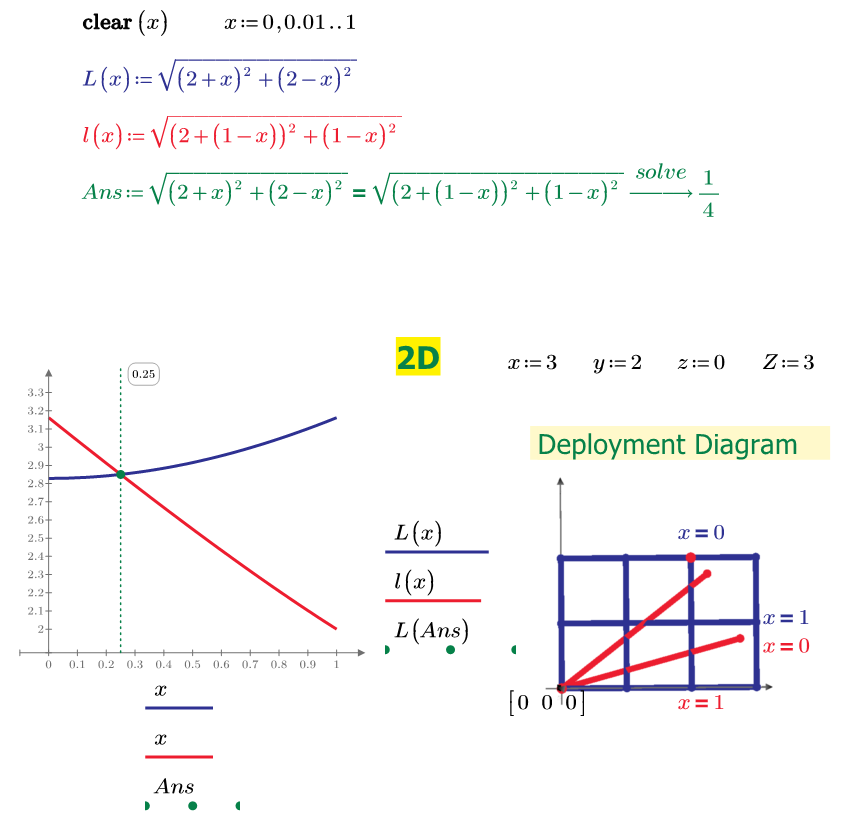
Original 1*1*2 cuboid has symmetrical plane, [0,0,0]-[0,0,2]-[1,1,2]-[1,1,0]. So, your 4 answers are right and as same as my results.
My reply's x:=2 y:=3 z=0 and Z:=3 means nothing. It only makes a plot of blue grid circuit for 2D 2*3 and shows two answers in red line.
Therefore, my equations only for cuboid with symmetrical plane. And for 3*4*5 cuboid, I have an answer but not sure it is true or not. 1*1*n cuboid's answer is already on the mathematics Web site. First thinking is may [0,0,0] to [1,1,2] be the largest distance. So, this is good puzzle to solve by Mathcad.
Tokoro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
IMHO the symmetry you mention does not necessarily mean that the point with the largest surface distance must lie in that symmetry plane. There could be two (or more points with the same largest distance which lie symmetrical to x=y. It is not the case in the task, but I see no compelling reason that it could not be that way. OK, there could be a compelling argument (which would then have to be formulated) that in that case there must necessarily be a point in the symmetry plane that has an even greater distance.
1*1*n cuboid's answer is already on the mathematics Web site.
??? Which web site?
According the 3*4*5 cube and the point with the largest distance from (0;0;0), here is what my sheet says:
Looks, like that in this case the opposite corner (3;4;5) actually is the solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
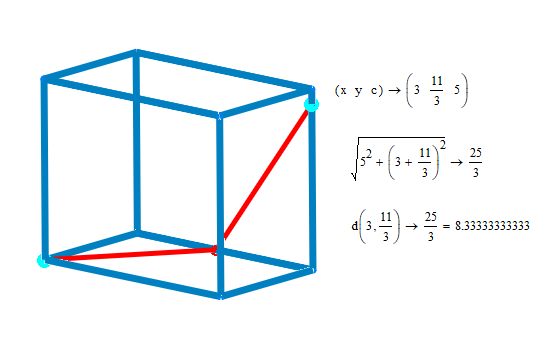
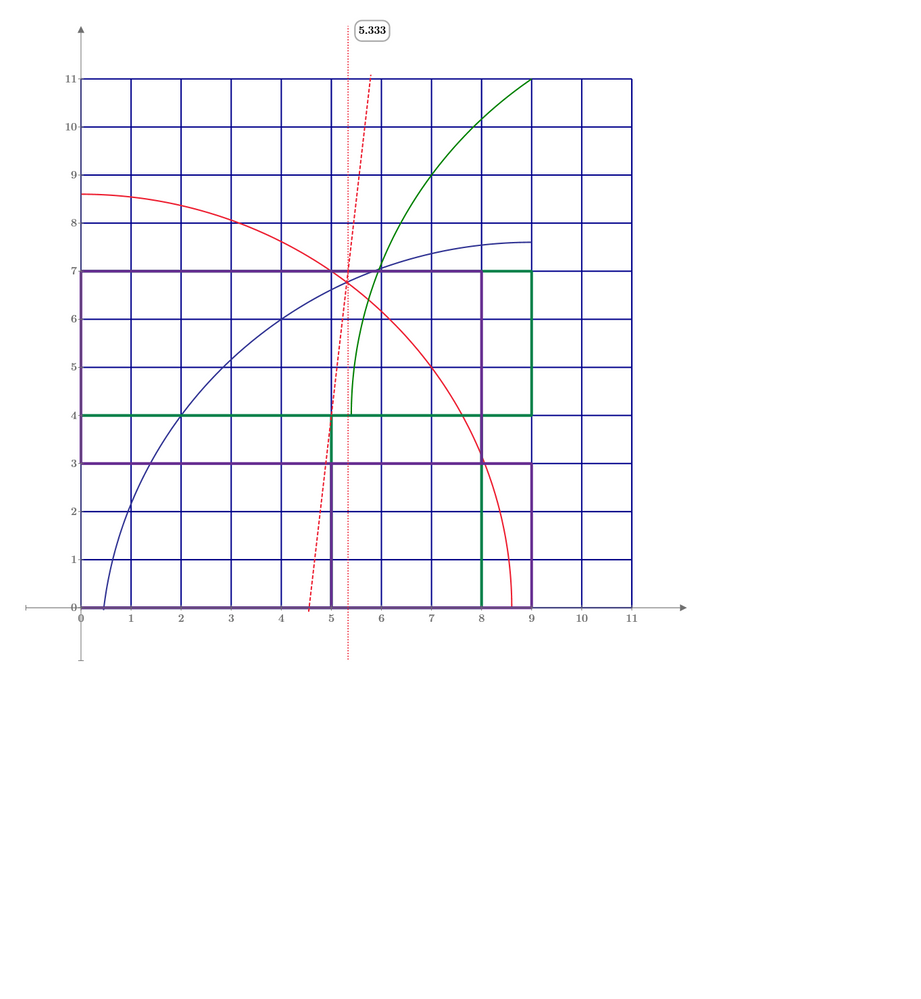
From the opposite corner (3;4;5) down 1/3 of y axis, therefore, (3,4-1/3,5) is my answer.
Please check the surface distance of from [0,0,0] to [3,11/3,5]
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is what I get
compared to
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. I only measure it from front side. But back side shows your result is the answer.
The final answer of 1*1*2 cuboid is
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The final answer of 1*1*2 cuboid is
? I guess that you are talking now about the pair of points with the largest geodesic distance possible?
I haven't dealt with that problem so far, but its clear that the distance must be larger than 3.
I see you are assuming the solution in the symmetry plane and you also assume that A(x;x,0) and B(1-x; 1-x; 2) with x is the expression you give in Ans ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, you are right. Plane symmetrical surface distance is solved for any 1*1*n cuboid.
My original 3*4*5 cuboid puzzle is point symmetrical and it means [0,0,0] and [3,4,5] are the symmetrical positions of most far each other.
I attached 1*1*n answer by Mathcad Prime 8.