Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Question on numerical calculation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Question on numerical calculation
This is more of a numerical analysis problem rather than a mathcad usage problem....
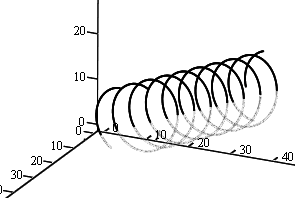
in this mathcad file, as you change the step size in the calulation of the locus of a helicoil like movement,
a bigger step size (less steps) actually gives you a spiraling outward helicoil and this behavior seems like exponential ! even at very small step size, a straight helicoil eventually become a spiral that seems to grow exponentially !
how do I know if a system would behaves this way apriori, i.e the error is exponential or linear ? I guess I have to do some derivative....
how can I determine when the error will exceed the tolerance?
when I do this calculation the first time I was expecting a stright helicoil but instead I got a spiral. It took me a few minutes to realize this behavior was due to the numerical error! How interesting! anyone have any recommendation on some good introductory reading on this topic (and simple to follow enough for bed time reading as I do not really have time to take a course on this thing)?
I just noticed this behavior first time ever while playing with mathcad...total something new for me...hmm, technically I know about it but never gave it a thought. wouldn't have noticed it if not for mathcad. I think our education should really teach kids to start using tools like mathcad in 3 or 4th grade once they can add subtract multiply and divide. Mathcad should not be marketed towards higher education and professionals only. You can teach kids some really interesting concept with a powerful computer. A lot of the math concepts is not difficult once you demonstrate it with a picture and graph. We can teach kids vector, calculus at a much earlier age. I think PTC can give MathcadPrime a more kid friendly interface and market it towards elementary school or middle school education, it is seen as a toy for many experienced mathcad users anyway ![]() . Make mathcad free for everyone under 18! and PTC will have much more revenue when they grow up.
. Make mathcad free for everyone under 18! and PTC will have much more revenue when they grow up.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe I am wrong, but I would not call this effect not call a numerical error, rather simply an aberration from the exact solution due to the chosen algorithm. There is a reason people came up with different, sometime rather complicated algorithms, for solving ODEs numerically. Simply walking along the tangents is a way of doing it, but will result in a lot of deviations from the real solution which will add up in an unwanted way.
You replace segments of the curve by segments of the tangents, that way I would expect a spiral effect every time, more or less visible to the naked eye.
Furthermore you don't normalize the tangent vector (use v/|v| instead of v), so if its growing, the effect is getting stronger - the distance, you walk along the tangent, is not the same in every step but getting larger, that way amplifying the spiral effect. Also that way the choice for omega has a great influence on the characteristic of the spiral effect.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Maybe I am wrong, but I would not call this effect not call a numerical error ...
I agree. A more advanced integration (using Adams/BDF) produces the same result - see attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree. A more advanced integration (using Adams/BDF) produces the same result
? Your sheet produced NOT that spiral effect.
BTW, what kind of Mathcad graphics error I am experiencing here? It looks like there are fewer points in the lower half but the position of the greyed area changes when I move/turn the graph.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
I agree. A more advanced integration (using Adams/BDF) produces the same result
? Your sheet produced NOT that spiral effect.
Yes, I've just read the original post more carefully! The expanding spiral with large timesteps is just the sort of inaccuracy one might expect from a simple Euler integration. It's numerical, but not one due to limited precision (just an intrinsic limitation of Euler's method).
BTW, what kind of Mathcad graphics error I am experiencing here? It looks like there are fewer points in the lower half but the position of the greyed area changes when I move/turn the graph.
I get the same effect. I don't know why!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
THanks WE and Alan
I Think now I would better appreciate the ode solve of mathcad and all those mathematician that develop all these numerical algorithm. How do people determine the result they see is real but not a limitation of the numerical method used like the one shown here? There must be some way people use to determine the accuracy.. Google time for me again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How do people determine the result they see is real
Thats a difficult philosphical question 😉
There must be some way people use to determine the accuracy.
Making good estimations for the error made in numerical approximations sure is not an easy and trivial task.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
... How do people determine the result they see is real but not a limitation of the numerical method used like the one shown here?
Testing some limiting conditions might help. For example, if you set alpha to be zero, you would expect to see a circle (I think!). The Odesolve, with Adams/BDF selected, does that better than the simple Euler method here, However, it isn't perfect (set omega ten times bigger, for example, to give it a harder task) - Odesolve with Radau is slightly better. However, no numerical scheme is going to be perfect!
Alan





