- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Question with rewriting or solving of isolating a variable on left side of equation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Question with rewriting or solving of isolating a variable on left side of equation.
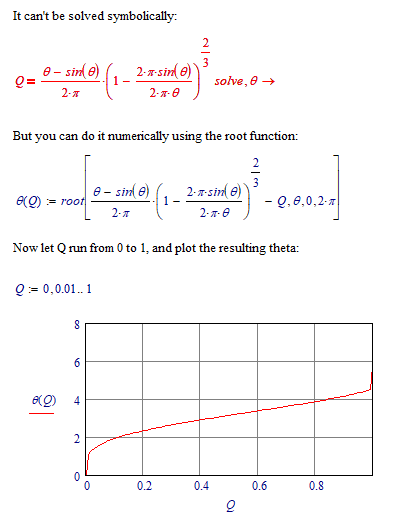
How can one re-write the equation with only theta on the left. I need to calculate theta when Q is known.
Will this be possible? Q is a ratio variable that rages between 0 and 1 and will be known from previous calculations. I know when Q=0.5 the Theta = PI and when Q=1 then Theta = 2*PI
Solved! Go to Solution.
- Labels:
-
Civil_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Normally you should attach a worksheet with your problem...
Prime 4 sheet attached.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Normally you should attach a worksheet with your problem...
Prime 4 sheet attached.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your response Luc.
I have been trying to solve it symbolically, so that one can get an answer without computational input.
Can you please just indicate why it cant be solved symbolically? (If Q is known)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
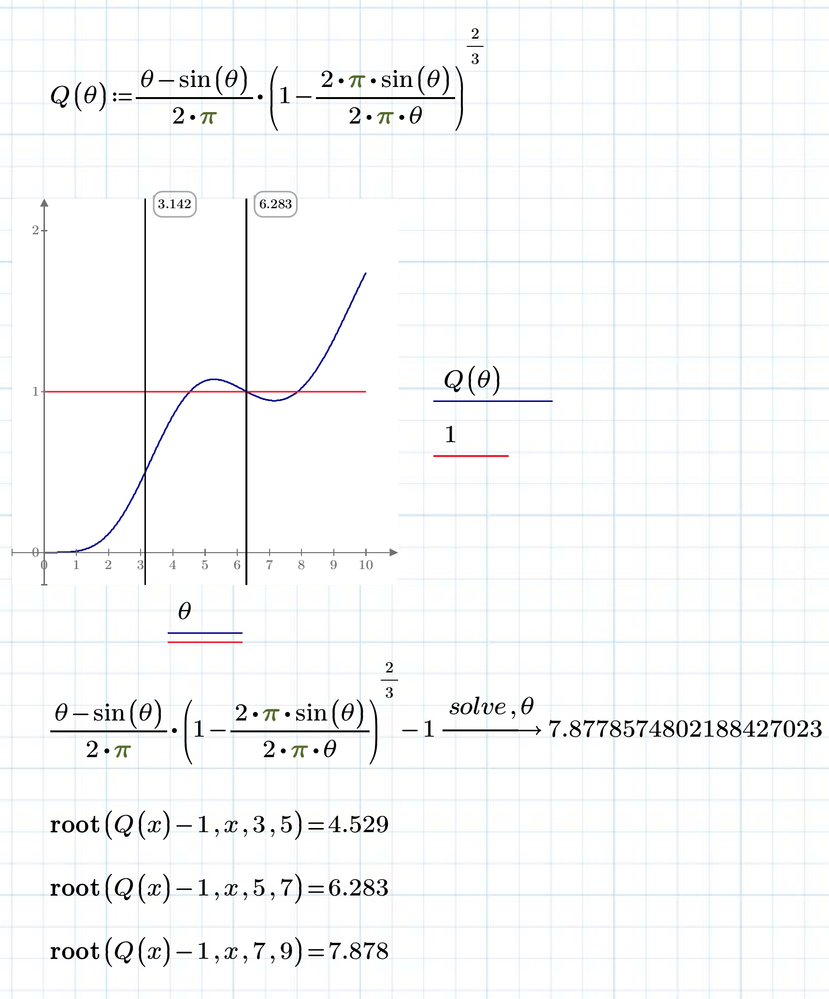
The answer is one or two or three values depend on Q.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
The answer is one or two or three values depend on Q.
No, as it was stated, that Q is only in the range from 0 to 1!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
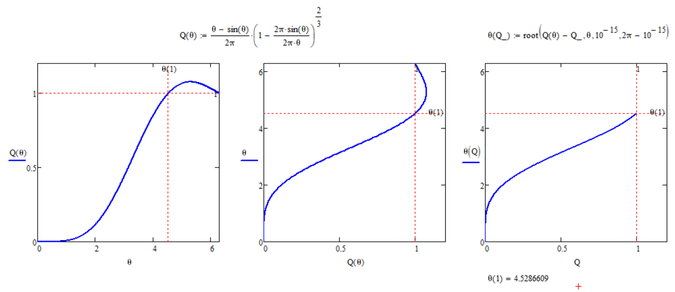
OK, to make it unique we have to limit Q in (0, 1] and theta in (0, 2pi)
Q=0 could only be achieved as limit q-> 0
theta=0 has to be excluded as it means a divison by zero and
theta=2 pi is excluded as otherwise theta(1) would have two solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Jan3 wrote:
Thank you for your response Luc.
I have been trying to solve it symbolically, so that one can get an answer without computational input.
Can you please just indicate why it cant be solved symbolically? (If Q is known)
Thats a mathematical limitation. An equation like yours can't be solve for theta analytically. You have to resort to numerical methods.