Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Question
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Question
Hy guys.
I have a problem with an algorithm.
I uploaded it so you can take a look. What changes do I have to make?
The thing is this: I need to find some dimensions so that a the value of N is equal to the volume (V) of the blue geometric form.
N I know. The volume i determined being the triunghiular pyramid minus the two with green.
The formulas I determined are aproximative, but the values must be similar to: S=1.03; t=1.09; p1=260.06; p2;90.11; p4=75.39. Yes, I know there is no p3.
A is the area.
So the question is: how to arrange those formulas so that the algorithm finds S,t,x1,y1,p1,p2,p3 so that N=V?
Thanks.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Had a second look at your sheet and of course Richard is right, you hadn't setup any iteration at all, just a bunch of equations.
You had an error in the volume equation - the whole expression has to be multiplied by 1/3, not just the first summand.
The problem is underdetermined. You can freely chose 2 of the variables (within certain ranges) and calculate all the others - e.g. you can make all values dependent on x1 and y1, or on p2 and p4 or, as I have done in the attached sheet, of t and S.
So also the volume is dependent on just those two variables. That means you can freely chose one of the two, lets say t (for the allowed range see the comments in the sheet) and calculate the other (S) so that the object has the demanded volume. You can look at the volume as a surface in 3D:
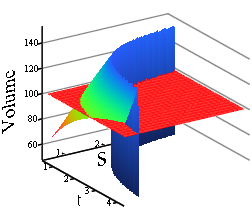
Mathcad's 3D plot doesn't allow us to suppress unwanted or invalid values, so in the above plot I have set all values corresponding to invalid combinations of t and S to zero. Thas the reason for that scarpe face.
So you can see that your problem has an infinite number of solutions (the red plane represents Volume=N).
You could add an additional constraint (like S=t or anything else) to get a unique solution.
As long as we don't do that we can also plot the solution curve (S over t) in a 2D plot
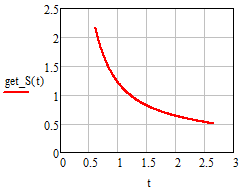
BTW, what is shown here is the complete solution curve - there is nothing more to the left or to the right of it!
You can also plot the other values, e.g. see p1 here
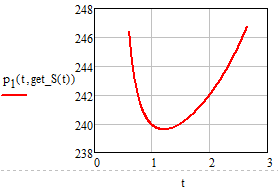
and as you can see it weill never go up to 260, as you wrote in your initial post - at least not with the values for L, B, Mx etc. you provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Setup a formula for the Volume in question which should be equal to N and use a solve block (given ... find()) to get your parameters, You are searching for 5 variables and only have 1 equation (V=N)? Guess there will be a lot of solutions!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All the values have a formula depending on the other coefficients. The N=V is a condition.
I just need to arrange them in the algorithm so it may run.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What is N, and how is it related to the other parameters?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, it is actually a force. It is used to determine p1 and from there p1 is used to determine p2 and p4.
And N must be equal to the volume determined by the formula from the application.
I need to arrange the formulas in the algorithm so the programme can run. I tried some things but I get that a variable is undefined or other things like that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First from your writing I get the impression you want to implement an iteration. So you should use "while" instead of "if". You comparison fails because no values for S,t,p1,etc have been initially specified.
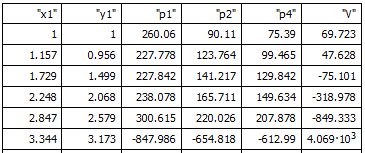
I changed that (you may chose to provide the inital values inside the program as you did with x1 and x2) but your program returns negative values for all p. I have streamlined your routine a bit and added a modified one where you can follow the iterations steps which should make it easier to find the error.
I also have the impression that in your iteration you mix old an new values. The volume is calculated by using the new values for x,y, and the p's, but the old values for S and t. Is this on purpose?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You did a lot o work. I thank you for that.
I must have seen this simpler than it actually is.
I entered the file but for some reason it is processing and doesn't give the result.
Yes I wanted it to be an iteration.
The main idea of the algorithm is that to determine the "segments" of a geometric figure so that the volume of that figure is equal to N. As you can observe all segments have a formula depending on other data.
The values I put out are the results that I must obtain. Well approximately those results.
I implemented values for x and y in an atempt to make the programme run. I actualy don't know the initial value of any of them. I know only: L,B,Mx,My,N and the figure shown in the image.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you don't have any initial values and don't want to chose arbitrary ones, you may consider doing the first iteration before the while-loop. But something with your iteration seems to be wrong. Either just a sign or something more severe - you may have to check your formulas. As you can see from the table, you iteration steps make the volume smaller, than negative and at last, boom! You will also have to reflect why you think that the very steps you implemented will bring you closer to the Volume you want to achieve. It doesn't look like a converging iteration. Depending on the initial values it may also happen that the routine doesn't stop at all!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's ok to give initial values. I just tried it, but it doesn't stop processing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your help Werner. I will review the algorithm.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's easier to let Mathcad do the iterating, using a solve block. However (as already pointed out by Werner), it seems there is an error in your equations somewhere. They can not all be valid as written, because they are not consistent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Had a second look at your sheet and of course Richard is right, you hadn't setup any iteration at all, just a bunch of equations.
You had an error in the volume equation - the whole expression has to be multiplied by 1/3, not just the first summand.
The problem is underdetermined. You can freely chose 2 of the variables (within certain ranges) and calculate all the others - e.g. you can make all values dependent on x1 and y1, or on p2 and p4 or, as I have done in the attached sheet, of t and S.
So also the volume is dependent on just those two variables. That means you can freely chose one of the two, lets say t (for the allowed range see the comments in the sheet) and calculate the other (S) so that the object has the demanded volume. You can look at the volume as a surface in 3D:

Mathcad's 3D plot doesn't allow us to suppress unwanted or invalid values, so in the above plot I have set all values corresponding to invalid combinations of t and S to zero. Thas the reason for that scarpe face.
So you can see that your problem has an infinite number of solutions (the red plane represents Volume=N).
You could add an additional constraint (like S=t or anything else) to get a unique solution.
As long as we don't do that we can also plot the solution curve (S over t) in a 2D plot

BTW, what is shown here is the complete solution curve - there is nothing more to the left or to the right of it!
You can also plot the other values, e.g. see p1 here

and as you can see it weill never go up to 260, as you wrote in your initial post - at least not with the values for L, B, Mx etc. you provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I managed to solve it.
Thank you for all your help. Werner, you really tried to solve the problem.
I will choose your answer as correct if it helps you with points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Air wrote:
I managed to solve it.
So you arrived at the values you mentioned in your first post? How? Guess you must have to add at least one additional equation to make it unique.
I will choose your answer as correct if it helps you with points.
Thanks, but I don't believe that many posters here really care for those points. There is nothing we could turn them in anyway 😉





