Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Radau , second order integration with non-linear system of ode
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Radau , second order integration with non-linear system of ode
Hello everyone,
I have a system of 3 non linear equations second order differential.
I'm using radau solving the following system : d/dt (phi) = f(phi)
But i would like to solve the system d²/dt²(phi)= f(phi) instead.
My f(phi) is a three dimensionnal vector with non linear . coupled phi's
For example (i've removed sensitive data and simplified problem)
How would you format D(u,Y) ? I've tried with the other solvers but it didn't solve. I'm stuck with Radau.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What are the initial conditions for the three components of dYdu?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attached is an example using Odesolve, with arbitrary initial first derivative values. Your system is very stiff!!
(The default integrator is BDF/Adams, but you can right-click on Odesolve and choose Radau if you want).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok thanks for the tip.
I've replaced the equations with the real system.and it's saying too many initial conditions. And doesn't solve.
I have 6 IC's
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
On the RHS of your equations you forgot to write the parameter parenthesis G2(t) - you simply wrote G2, etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok , it's working in the first sheet.
However when i'm transferring the method back to the second field. I have an error on G0 (too many IC's)
Here is the full sheet...
It's very long and it's at the end.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
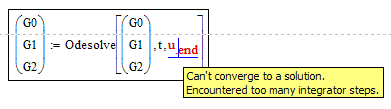
If you use only the result of the symbolic evaluation (the euqations itself) you get past this error, but you get a new one.
It only works if u.end is under 0.25, otherwise you get the following error :
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, you can cope with that error by increasing the number of intervals from the default 1000 to something like 90000 or higher.
But I am not sure if it would make much sense to go up with u as high as to 3 as you tried and if the numeric results of odesolve in that area would be much reliable. Especially as of the high frequency of your signals.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
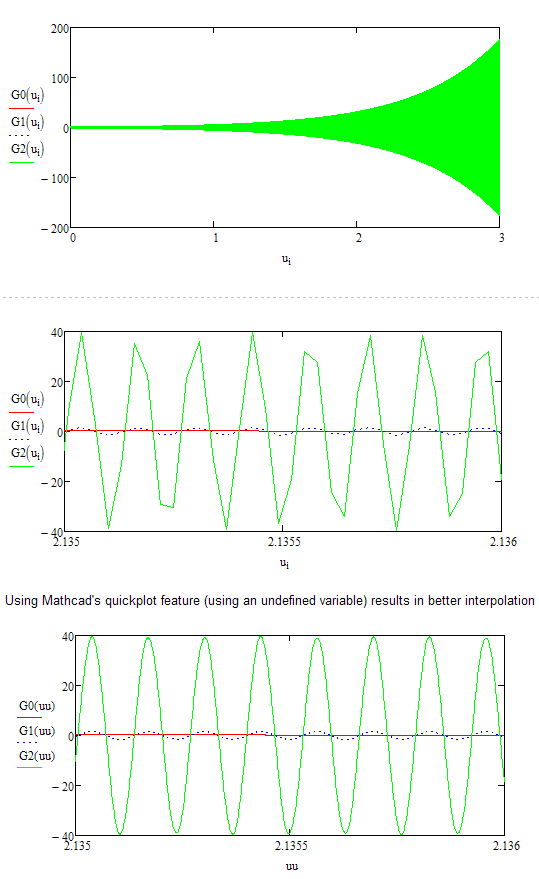
I've been looking at this problem in more detail. There are a number of issues.
1. The independent Radau integrator just integrates once, so it doesn't make sense to compare it with results from integrating twice with Odesolve!
2. You've also set different initial conditions for Odesolve, which doesn't help!
3. If we use comparable initial conditions and integrate just once with Odesolve, using its Radau option, then we get the same set of results as from the independent Radau version.
4. However, if we choose the BDF/Adams option we get a different set of results.
5. If we reduce TOL to, say, 10^-8 (the default is 10^-3), then the Radau option in Odesolve now gives the same set of results as BDF/Adams - different from the independent Radau version!
See attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you use the Radau solver it does work. i have to compute u.end till tlast which is around 0.35. And solves.
Is there a way to get past this error without copying the whole thing equations again and again?
I'm making this CAD as a routine check for deflections compared with other FE softwares
I have a few steps after the solving and it's a bit annoying to have this.
The bdf/radau signal diverge? Let me check that out.





