Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Real and positive root needed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Real and positive root needed
How can I gat a Real and positive root - see the picture and attach (Mathcad 15 and, pardon, Mathcad Prime 2.0)

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But the best solution is from Mathcad - a complex of symbolic and numeric math:
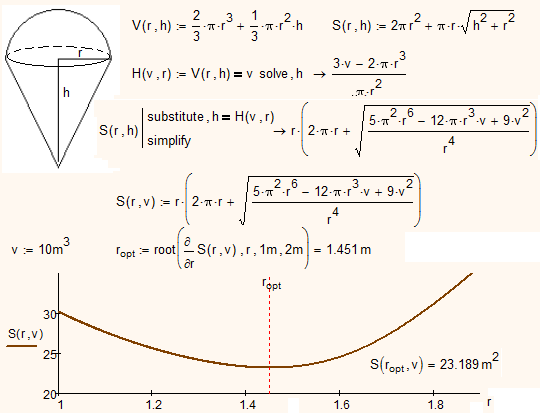
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First thought was to use the modifier "assume,ALL>0", but the result is going crazy that way and i don't know why - sorry. You can only see it in the Prime version, as 15 say that the result is too big to display.
Maybe the conditions you see in doing so help you - they didn't help me understanding the problem.
At least you get a single result with "assume, ALL>0" if you assign V a value before solving.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, but it is not a solution. I need in the answer V not m.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
Thanks, but it is not a solution. I need in the answer V not m.
Yes , I've seen that you used the generiv V to proof that the ratio r/h is sqrt(2). But then in this case it should be clear that this ratio is not dependent on the value of V.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is really a tough one (with/for Mathcad).
You have to simplify the problem by hand from the order 12 down to an order three equation to make it work - Blame on you Mathcad!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner. I can do it "by hand" but I would like to do it by Mathcad for others same problems.
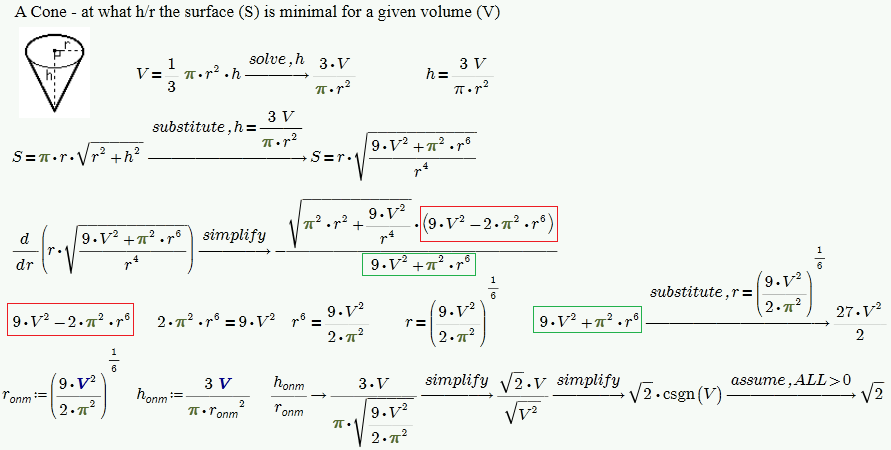
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or
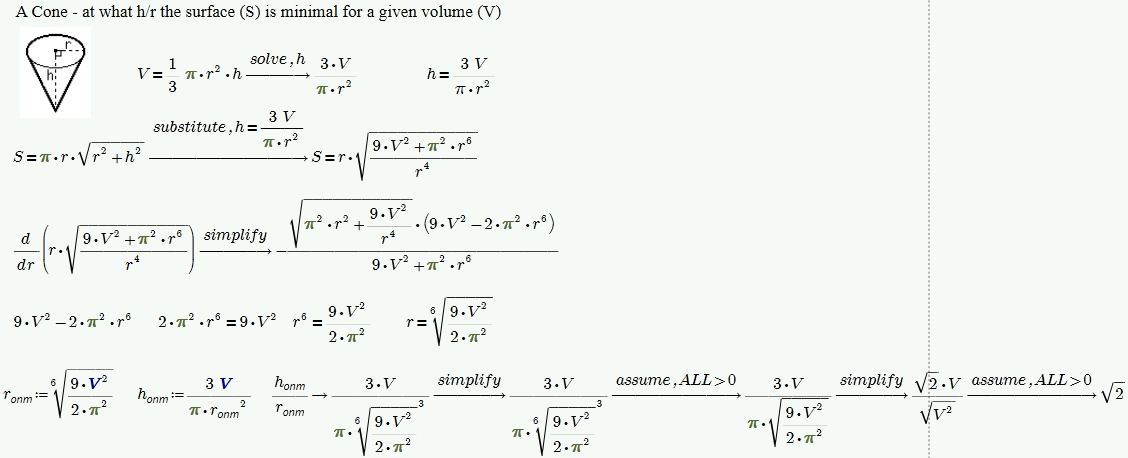
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
Thanks, Werner. I can do it "by hand"
I didn't doubt it 😉
I was not trying to sell the manually simplification of the equations as a solution to your question (then it even would have been easier to simply pick the postive real solution from your vector of 12). Just demonstrated that "assume" only works if the expression is simple enough. If you look at the last two expression of my last screenshot - It not clear to me why V^(1/3) seems to be OK and is evaluated as such but V^(2/6) oviously is not. Don't see any other expression which could cause that behaviour.
I had already writte in the past quite often that assume unforunately does not work very reliable.
It even gets worse - just spotted a difference between MC15 and P2. In Prime even the last line would not evaluate the way we expect it. If you write assume,V>0 you get the three solution, if you add r>0 or r=real ... boom!!! I have no explanation

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about the following? It often helps to get rid of square roots! Still a little convoluted though!
Alan
Actually, you don't need to square f to get the above solution. I should have inserted a 'simplify' after f^2 to make it obvious (if it wasn't already!) that substituting r6 for r^6 is a sensible thing to do.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!
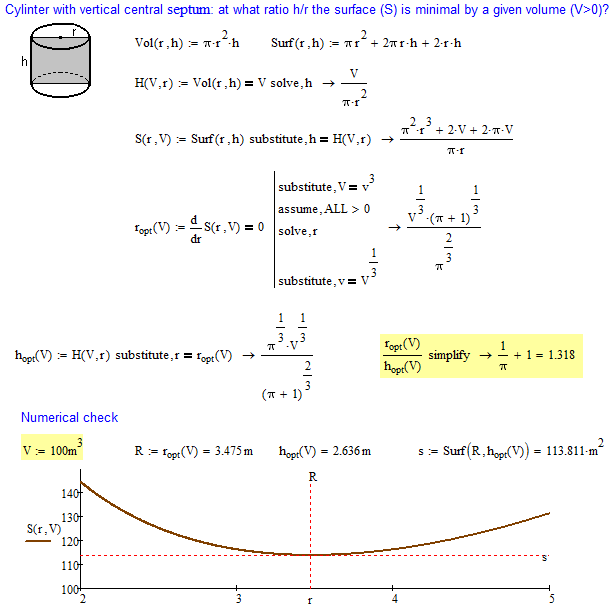
Cylinder d = h
Cylinder without top r = h
Cone without top h/r = sqr(2)
Cone with top h/r = 2*sqr(2)
And what about symbolic solution of this problem:
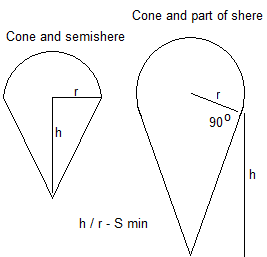
And what about symbolic solution (R/H -? H/L-?) of this problem:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens schrieb:
How about the following? It often helps to get rid of square roots! Still a little convoluted though!
Alan
Actually, you don't need to square f to get the above solution. I should have inserted a 'simplify' after f^2 to make it obvious (if it wasn't already!) that substituting r6 for r^6 is a sensible thing to do.
Nice idea, but calling that substitution "sensible" is kind of understatement ![]() .
.
What about this substitution(I haven't tried it in Prime). Of course all of this is specific to that special example and we will have to admit that (while I think it should be) Mathcad is not powerful enough to be an appropriate tool for that kind of tasks. In the example V^(1/3) seems to be the problem, therefore that special substitution.
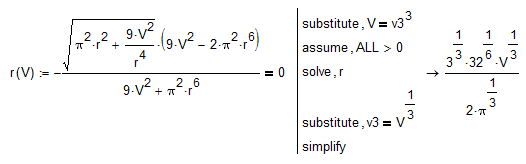
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks again!
It is very tempting to have an analytical (symbolic) solution, but must be content with a numerical answer and combine symbolic and numerical mathematics:
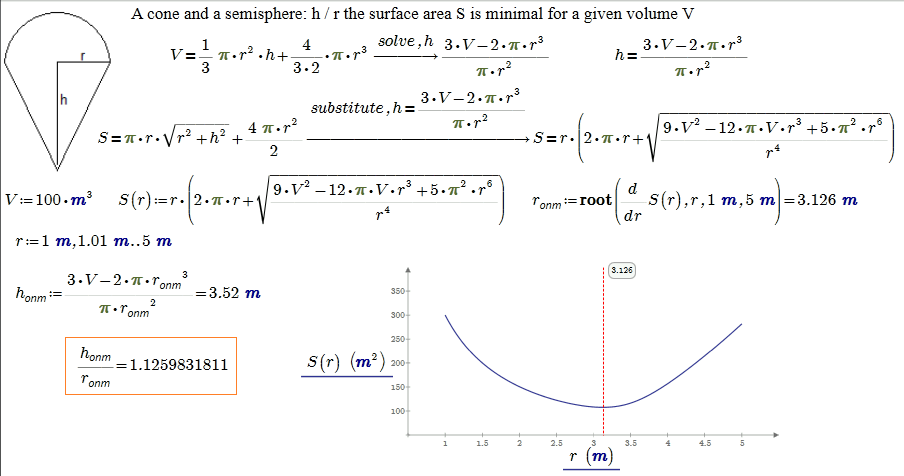
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is very tempting to have an analytical (symbolic) solution, but must be content with a numerical answer and combine symbolic and numerical mathematics:
Guess that's true. I've tried to get a symbolic solution to that very problem, but I could not wait for the last (now disabled) expression to finish to evaluate. Don't know if Mathcad will ever come to an end. Maybe I'll try it on a better machine with more memory next week.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Is it a paradox? See the attach!
Where is the paradox? I do not see the paradox.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The cylinder without top cover ("a glass") at r = h is a minimal surface. If this hat "wear a hat" - cover it with a hemisphere, then such a composite body with r = h is a minimal surface.
We inverted cone without a cap ("Cone Glass" Bottoms up "") if h / r = sqr (2) will be a minimal surface. If this sonus "wear a hat" - cover it with a hemisphere, then such a composite body optimum proportion of change - will not be a minimal surface with h / r = sqr (2). Why?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
The cylinder without top cover ("a glass") at r = h is a minimal surface. If this hat "wear a hat" - cover it with a hemisphere, then such a composite body with r = h is a minimal surface.
We inverted cone without a cap ("Cone Glass" Bottoms up "") if h / r = sqr (2) will be a minimal surface. If this sonus "wear a hat" - cover it with a hemisphere, then such a composite body optimum proportion of change - will not be a minimal surface with h / r = sqr (2). Why?
I wouldn't had expected the same ratio.
Difference may have something to do with the fact, that for the cylinder height and surface are proportional while for the cone they are not.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
Thanks!
I have checked it on one trivial case:
Yes, function ar much more friendly in that case 😉
Did you give the original file (Cone_Semisphere) a try? Did it finsh with an error?
I guess that both files won't work with Prime2 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Did you give the original file (Cone_Semisphere) a try? Did it finsh with an error?
Try please the attach!
I will try to solve this task tomorrow with Maple.
Maple has a function min for this task.
Now I ran this program and promised to my home laptop, which will solve the problem if it is, then I will buy this laptop a new case - in crocodile leather. And I am going to walk with my dog. I'll come back and see whether the problem is solved.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try please the attach!
What for? Thats basically my sheet which I could not wait finishing. Just was curious if it worked for somebody with a better machine and/or more patience.
I will try to solve this task tomorrow with Maple.
Maple has a function min for this task.
Would be interesting if Maple could arrive at a somewhat better simplified exact symbolic solution compared to the one I gave in the file. That was derived as a quick hack with good old and hopelessly outdated Derive6.
Now I ran this program and promised to my home laptop, which will solve the problem if it is, then I will buy this laptop a new case - in crocodile leather. And I am going to walk with my dog. I'll come back and see whether the problem is solved.
According to my experience you should allow your dog a rather lengthy, long walk.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
That was derived as a quick hack with good old and hopelessly outdated Derive6.
I didn't realize anybody had Derive 6, Werner! ![]()
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I didn't realize anybody had Derive 6, Werner!
Stuart
Think thats the answer to a question I posed just before in another thread 😉
I used Derive a lot and still have it installed. I loved it already in DOS times and the keyboard shorcuts were burned in my brain the same way as those from Wordstar. The whole program on a single floppy and so much math - that was math made in Honolulu.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I will try to solve this task tomorrow with Maple.
Sorry, no sollution in Maple too ![]()
But Mathcad can solve same problem (see the picture below and the file - can we more simplify the symbolic answer?).
Do you have some others problem of bodies optimisation? I will be glad to see them!
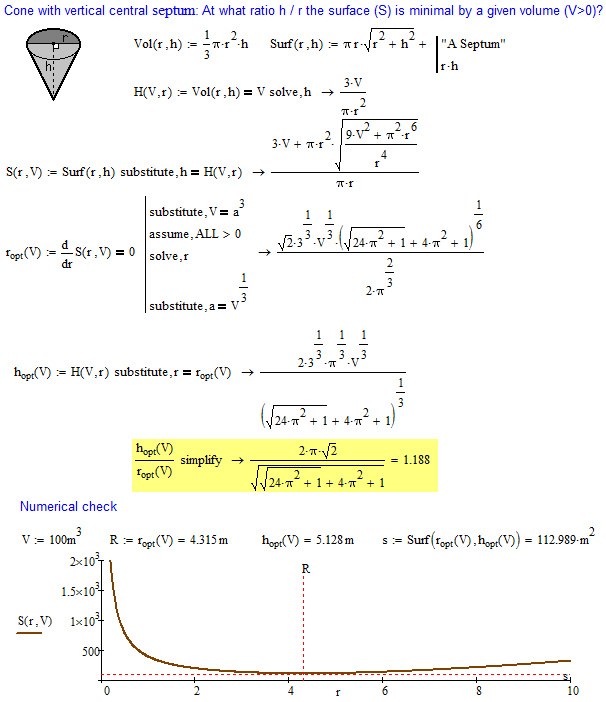
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
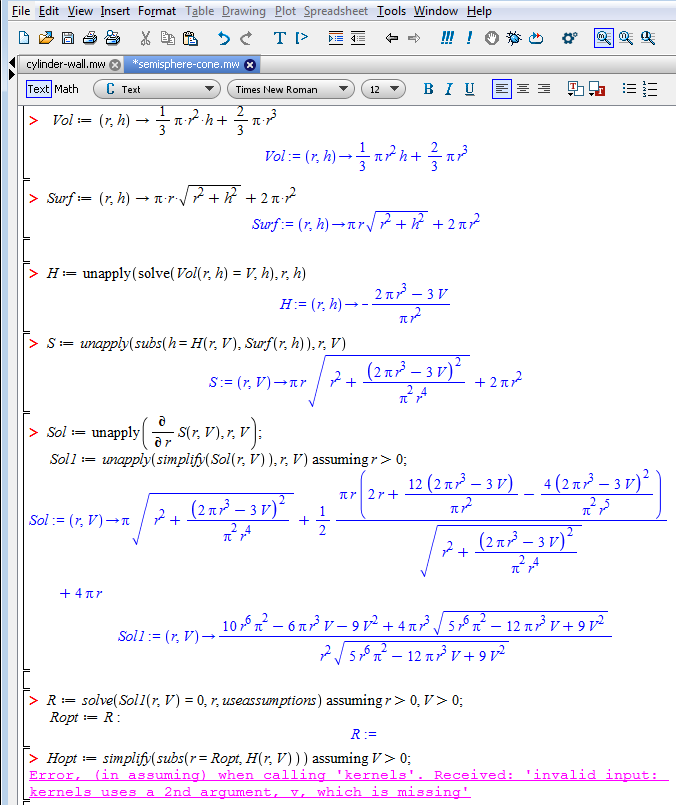
But Mathcad can solve same problem (see the picture below and the file - can we more simplify the symbolic answer?).
Can't get Mathcad to make the denominator squareroot-free. Ther are not too many way in Mathcad to get control over the outcome of an simplification.
The expressions below are equivalent, one may argue about simplicity.
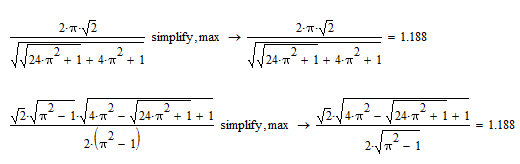
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jan Kowalski wrote:
Result in Mathematica 9.
In Semishere-Cone.xmcd file No symbolics result.
In Maple too ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
Jan Kowalski wrote:
Result in Mathematica 9.
In Semishere-Cone.xmcd file No symbolics result.
In Maple too
I guess that Mathematica would do the job (don't have acces to at the time) and I am really happy to see that good old Derive did the job quite well.
Mathcad would make a nice frontend for Derive. Dreaming of being able to switch in and out different symbolic engines in Mathcad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jan Kowalski wrote:
Result in Mathematica 9.
In Semishere-Cone.xmcd file No symbolics result.
It (Mathcad vs. Mathematica) is a good topic for same conference:
https://www.wolfram.com/events/technology-conference-eu/2013
And see elso Jakov Kucan blogs Mathcad vs. Excel, Mathcad vs. Java etc






