Reminder of an almost forgotten sentence ;-)

[AlfredFlaßhaar]

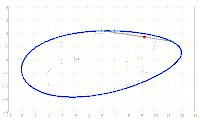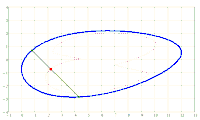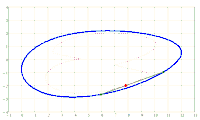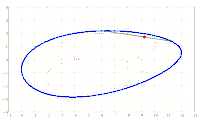
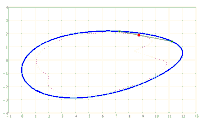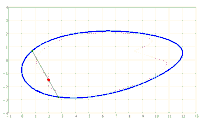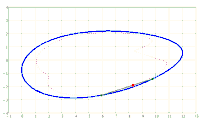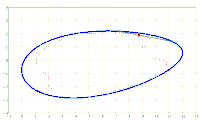
Given an ellipse E in the Cartesian coordinate system with the semi-axes a > b and the equation

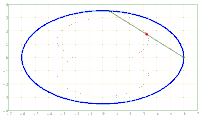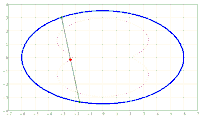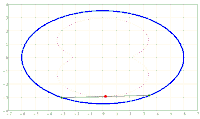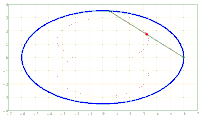
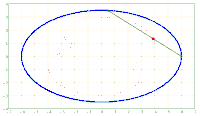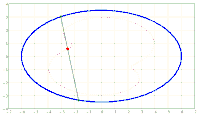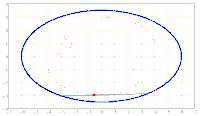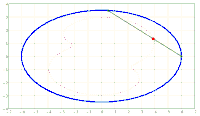
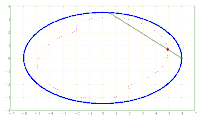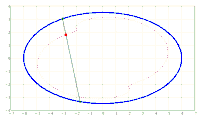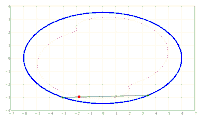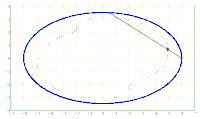
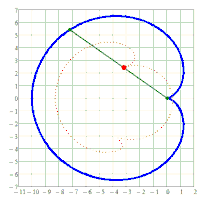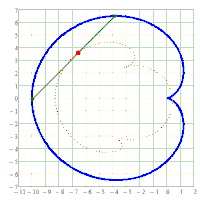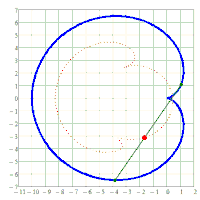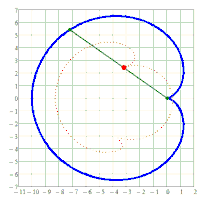
x^2/a^2 + y^2/b^2 = 1. A chord AB of fixed length s < 2*b is considered. Let the point P be fixed on the chord so that the chord is divided into the segments AP = u and PB = v, i.e. u + v = s. The points A and B should now be moved on the periphery of the ellipse in a rotational direction while maintaining the chord length s and its pitch P in u and v. During this movement, point P describes a closed curve K.

The content of the annular area bounded by E and K is sought.

[Werner_E]

You are talking about Hamnet(t) Holditch's theorem from 1858!?

[AlfredFlaßhaar]

Yes, that is the “betrayed” result. The only thing missing is the symbolic solution. When I heard about this many years ago, I was impressed by the simplicity in the general case - a convex ring-like surface is easily calculated after sweeping through a tangent path.

[Werner_E · Accepted solution]

I believe that Holditch was only specifically concerned with an ellipse and the case s=(a+b)/2 = u+v with u=v. I am not sure about that, though.

Its surprising that the area does not depend on the type or size of convex, closed curve used and is always  u*v*pi.

Good luck for dealing with the more general case using Mathcad!

I am not sure if the symbolics in MC14 or MC15 is capable enough to deliver a general proof.

EDIT: Actually I found (and still find) it hard to implement a way to find numerical solutions for the new curve created.

Some nicer animations can be found here: Courbe de Holditch

 

 

 

 

 

[SQ_11052426]

Thanks for sharing this and helping.

[AlfredFlaßhaar]

You are right, I have seriously underestimated this task. Unfortunately, my programming skills are not sufficient to present a solution here. Therefore, I must restrict myself to the theoretical remainder. I was impressed by the thinking behind Holditch's theorem - a tangent sweeps out a general ring of areas, the content of which is calculated using a simple formula. Somehow this fits into the classic line of Guldin and Cavalieri, which leads in the direction of integral calculus.