- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Rnd in Mathcad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Rnd in Mathcad
I think the rnd function (a procedure) in Mathcad is not so good ![]()
What can you say about it?
See please this animation http://communities.ptc.com/videos/3806
and this two pictures:
Coin

Dice

- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I think the rnd function (a procedure) in Mathcad is not so good
Why do you think so?
What did you expect for the coin toss? Precisely 50%???
The probabilty that with 10^7 tosses you get exactly 50% heads is just about 0.025% so I wouldn't trust the random number generator if it would yield exactly 50% most of the times.
On the other hand - the probability that the percentage of heads up is inbetween 49.95% and 50.05% for 10^7 tosses is as high as 99.84% and that fits perfectly to the result you achieved.
EDIT: The coin toss routine could be written much more compact

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See please the animation.
I think the point must go to the line at n-> infinity.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
See please the animation.
I think the point must go to the line at n-> infinity.
For n->infinity, yes. For n=10^5 not necessarily.
But its disturbing the the calculated value is always too high.
But then, we don't see how the random numbers are generated and how it is decided if a point is inside.
BTW, I have programmed that Monte Carlo pi finding quite a number of times using different programming labguages and different compilers and it was somewhat disappointing every time. Its a very slowly converging method.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry more compact but not so simple for an understanding
Thats true, but your point was to prove that the randon number generator in Mathcad does not work to your expectation and not to provide a sample program to be used in a basic programming course, right?![]()
And what about 2 dices?
Interested in another harder to understand routine? ![]()
Of course we can compact that too:

The drawback of both routines is that a full vector is generated first hand and there is a (memory) limitation for creating vectors which prevents using much larger numbers for n than those given in the screenshots.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner!
I would like to translate into English my article "Tripartite duel in Monte Carlo" from the Magazine "IT in school".
The rnd routine is the main point of the article!
See pictures here http://twt.mpei.ac.ru/ochkov/Mathcad-15/duel-pdf.pdf
The begin of the article
There is one joke. Student wakes up every morning and thinks of throwing a coin, "the winning eagle - will sleep more on the right side, rolled tails - lie on your left side, on the edge of the coin will fall - go to college, and hangs in the air - 'll coursework."
Joking aside, we often have to toss a coin - real or virtual , to randomly select one of two equally likely possibility . Football referee, for example, before the match is flipping a coin to determine which team to give certain gates. Chess player before the game in one hand grips the white pawn and the other - black and offers an opponent choose "one of two equally likely possibility" - to determine who will play the white pieces , and who - black . Shuffling a deck of cards or dominoes stirring, again we give ourselves to chance. And from this , the will of the case may depend very much... Even the person's life, if you remember the title of this article. And why not a simple ( two-sided ), and unusual ( tripartite ) duel, and even in Monte Carlo!? The fact that the problem of the tripartite duel is described in many books , such as [1, 2 ], which provides one of the particular solutions of this problem , obtained by logical reasoning . We consider a more complete solution to this problem on a computer Monte Carlo ( Monte Carlo method ) : simulate a single duel , spend quite a lot of her time and calculate the number of wins in these duels each participant [3]. If these numbers are divided by the total number of duels, and the result will be the desired probability victories.
But we begin with simple tasks bezkompyuternoe decision known.
Let us remember our lackadaisical student from a joke, using a computer to flip a coin many times and count how many times the winning eagle, and how much - tails. Fig. 1 shows the corresponding computer program - OrelIliReshka function with argument n (number of tosses of a coin), which returns the probability of coming up heads or tails .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I cannot duplicate the problem/error your animation shows but without seeing the code we cannot tell if there is an error in the sheet or what else could cause that effect.
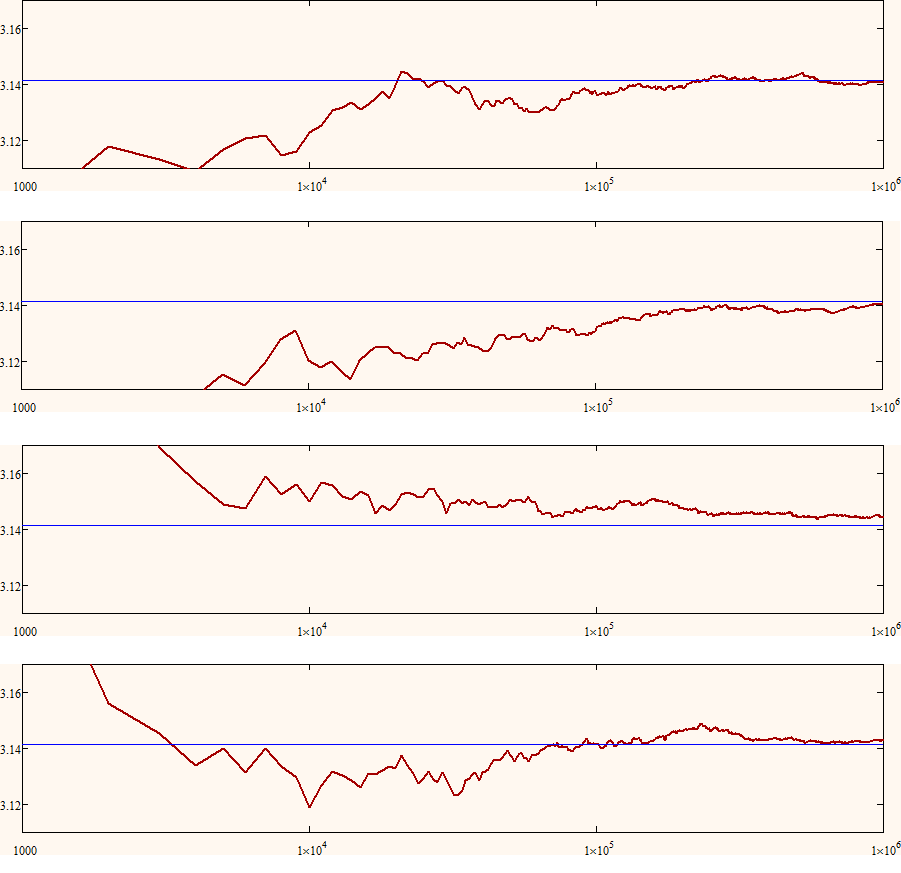
At least I reproduced the Monte Carlo calculation of Pi and see a slow but good convergence.
See below some screenshots from different runs in a log scale.
An animation using a linear scale is here: http://communities.ptc.com/videos/4527
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Accuracy in Monte-Carlo simulations tends to improve with the square root of the number of trials (see http://www.cs.nyu.edu/courses/fall06/G22.2112-001/MonteCarlo.pdf for example), so to improve by 1 extra decimal place (a factor of ten) one needs 100 times as many trials. Typically, the Monte-Carlo simulation of pi gets around one decimal place accuracy after 1000 trials. This means that one might expect, at best, 2 decimal places of accuracy after 10^5 trials and three decimal places of accuracy after 10^7 trials.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the insights and the interesting article.
I think we see the behaviour of the Monte Carlo simulation you described pretty well if we go up to 10^7 points like in the videos (Valery needs animations ![]() ) here:
) here:
Logarithmic scale: http://communities.ptc.com/videos/4532
Linear scale: http://communities.ptc.com/videos/4533
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Thanks for ... the interesting article.
At first I was thinking that these words are about my article "Tripartite duel in Monte Carlo" ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, my zero knowledge of Russian language prevents me from commenting on your article.
My post was a reply to Alan's.
After all this thread is about your Monte Carlo simulation which in your opinion is too slow or not at all improving and about Mathcad's random number generator which you thought is responsible for this.
Alans remarks clarified that what you see in your simulations is just normal behaviour and that you will have to increase the number of trials significantly to see a small improvent and the article he referred to is a good one and worth reading. My animations try to demonstrate exactly that by showing the simulation with 10^7 trials. We see a nice convergence but if you look where we are at 10^5 trials (which is where you stopped your simultation) - better seen in the animation with the log scale as this is already at FRAME 4 of 499! - you see you simply stopped you animation too soon.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
I cannot duplicate the problem/error your animation shows but...
See (optimize) please attach.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See (optimize) please attach.
As far as I can see there is no error in this sheet which could lend to wrong simulation results. So the above said is still true: You cannot excpect a much better result with "just" 10^5 trials - thats all. You simply stopped your animation too soon. If you want the approximation to be closer to the real value, you will have to increase the number of trials significantly.
One thing I would optimize is the precalculation of Delta like this
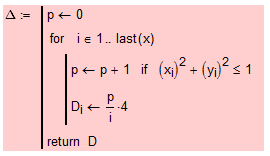
The way you did it is very time consuming as the count starts over from scratch for every vector element.
Another thing I tried to optimize was to get rid of all the submatrix commands to speed up animation, but I ran into Mathcad's plot limit when I increased the number of trials (see: http://communities.ptc.com/message/228788#228788)
So I just changed a few minor things like making the number of trials and the maximal frame number easily selectable in one place; tried to make the total number of point for each animation frame a better "round" number and got rid of the a little bit odd nonlinearscale replacing it by a linear and a logarithmic one.
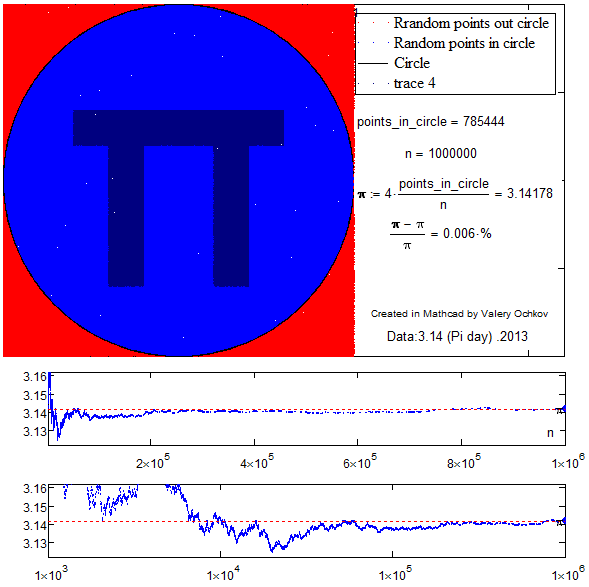
For a number of trials as high as 10^6 I also had to adjust the size of the points plotted to be as small as possible.
If you intend to increase that number to something like 10^7 you will have to change your sheet significantly as you will run into memory problems - too many big vectors, too many points to plot, etc.
Also you would have to reduce the pointsize again as to not reveal the pi-sign too soon, But that's not possible in the 2D plot so you will have to workaround that problem, In my animations with 10^7 trials here (http://communities.ptc.com/videos/4533 and http://communities.ptc.com/videos/4532) I favored a fading effect. If a point is chosen by random, it is not plotted immedeatly but is faded in in more than 100 steps of transparency. So the simulation will have to hit a point over 100 times to get the picture underneath fully revealed.
Here is an animation using your sheet with 10^6 trials http://communities.ptc.com/videos/4538
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner! I see you have a powerfull computer. Can you check the program in attach?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Werner! I see you have a powerfull computer
Not at all! It was a slow single core notebook with just 1 GB of RAM 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But check please the sheet (duel).
May by you have fresh ideas.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Check for what? Is there any specific problem?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Check for what? Is there any specific problem?
For model!
And for rnd in the model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, I loaded your sheet and it seems to calculate pretty well to the values from the book you mention. I had to cancel operations as the last few expression seemed to calculate "endless".
Prime files are so slow and cumbersome to navigate and edit and even cancelling calculation is so much more difficult. In Mathcad i would just press ESC and eventually Mathcad would ask me if I want to cancel.
In Prime a first have to switch to the appropriate ribbon and then press the button - not so easy if mouse and keyboard are hardly reacting to anything because Prime uses up most ressources. Again I confirmed why i don't like that crap.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
In Prime a first have to switch to the appropriate ribbon and then press the button - not so easy if mouse and keyboard are hardly reacting to anything because Prime uses up most ressources. Again I confirmed why i don't like that crap.
Do you only now break Prime![]()
Smetime we must press Ctrl+Alt+Del![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Do you only now break Prime
Smetime we must press Ctrl+Alt+Del
No, I had to cancel operations quite often in Prime and it was a hassle most of the time
Yes, sometimes I wasn't able to go to the calc ribbon and also had to kill the task via taskmanager.
I am not saying that mathcad 15 is perfect with all those processes being left in memory ever so often, but Prime definitely is worse.
And no, I won't buy new hardware just to be able to run new program with half the speed and half the features.
"half the features"? Sorry, that was unfair against Mathcad 15.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not getting your point..It is really difficult to understand..What are the simplest form of it? Any one aware about teh functions of two factor authentication in Google apps ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What's wrong with this assessment of the rnd function:
The results come pretty close to what they should be.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator







