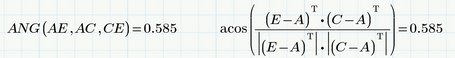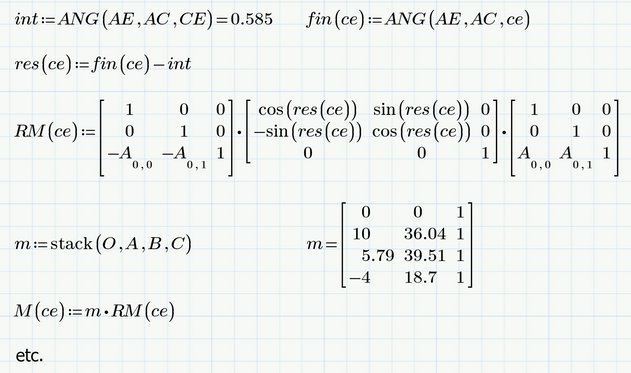Rotating a set of co-ordinates values using rotation matrices over a range of angles .

[KishoreK]

I am trying to Rotate a set of co-ordinates about a point using rotation matrix  , over a range of angles , I can do it in excel with ease using the data tables and i can get the values for different angles . Is there a way for using the same DATA tables of excel in MATCAD. Attached the file and i would like to vary the length of "ce" for a range of values and get the dependent values of L(H,I).

Thanks in advance

[Werner_E]

Its not clear to me which results you are looking for. So just a few remarks:

1) To calculate the length of a vector you may simply use the "absolute value" or the "norm" operator. If you have row vectors, you have to turn them into column vectors first by using the transpose operator. That way you can get rid of or rewrite your function "L"

2) You may get the angle between two vectors a bit easier. Again, you have to use column vectors.

3) If you want to calculate anything dependent on a certain variable like "ce", you have to turn your calculations into functions of "ce".

At the end you may call the function which gives you the result)s) you are looking for with a vector of different "ce"-values as argument to get a list of associated results.

BTW, it looks like you problem is 2D only. So I wonder why you add a third coordinate z=1 to all your points!?

Immediately after defining "m" using the current values of O,A,B, C you redefine the meaning of O,A,B,C depending on the just calculated value of "m". Its not clear to me why you really are trying to achieve, but I guess it may help if you reconsider your calculations.
Keep in mind that Prime reads the sheet left to right and top to down like we do. So a calculation down lower down can't influence a calculation prior to it. Way out of this "problem" is to define functions.

[KishoreK]

Thanks . The solution was pretty easy.

[Fred_Kohlhepp]

Adding a "Z" component to a two dimensional problem is an easy way to create a vector normal to a known vector (by vector cross-product.)

[Werner_E]

---

@Fred_Kohlhepp wrote:

Adding a "Z" component to a two dimensional problem is an easy way to create a vector normal to a known vector (by vector cross-product.)

---

Yes, cross product with (0,0,1). Adding that dummy dimension might also be helpful in calculating the area defined by two vectors (parallelogram or triangle).

Homogeneous coordinates can be quite useful in other respects, too - especially when it comes to transformations. But I did not spot any use of the extra z component in the worksheet, so I wondered why it was done.

EDIT: Ahh! Just looked again and noticed the calculation of RM 😉