Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
SSE vs. ERR variable at a MinERR Solveblock?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SSE vs. ERR variable at a MinERR Solveblock?
Hi Friends,
one short Question:
Is - for an nonlinear model - the ERR variable at a MINERR Solve Block the same as the Sum of Squared Errors? (SSE)
I have different values there.
Thanks for helping and answering.
Walter
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Walter,
Compare SSE and ERR^2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The attached sheet should help but Viktor already explained the relationship.
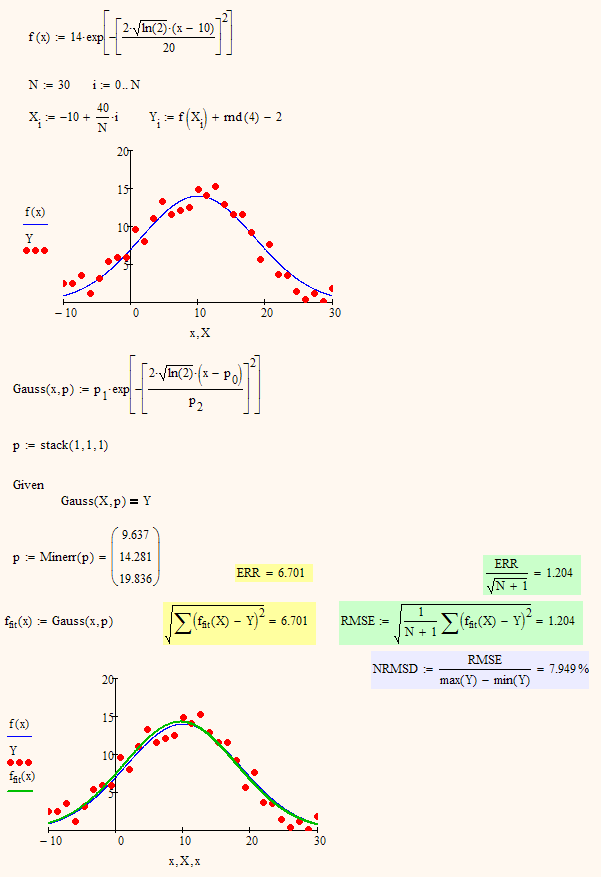
Regards, Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot! I also thought that minimizing SSE would be the same as

I think the proper Fitting with least errors is minimizing SSE, right? But why do I not get fine with my sheet? In my second sheet is fine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the proper Fitting with least errors is minimizing SSE, right?
No. Minimize the residuals, and use the Levenberg-Marquardt algorithm. Passing the SSE to the LM algorithm messes up how it works, and you get less than optimal results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks that answers my question I already had posted here for a while.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner, thanks a lot for your nice sheet. I have adapted it with my model and worked fine. I really a little bit confused why the mentioned sheet will not work.
Thanks
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
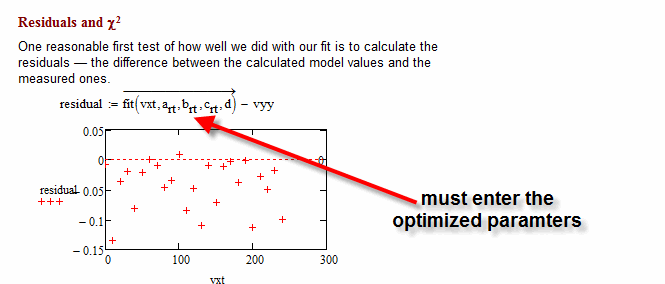
Sorry, I found it. I must enter of cource the optimized parameters in the SSE calculation. Sorry for bother you all. Thanks anyway for your friendly answers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is your SSE function. It does not use the formal arguments a,b,c on the RHS. It should look like this
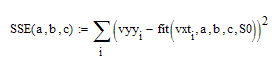
Instead of
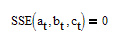
you may also use
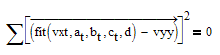
or you may like to define your SSE function that way.
With any of these methods you get an SSE of 0,062 which seems to be pretty good, especially compared to the SSE=0,103 you get with the values 35 / 15 / 0.6 from MMA(?)
You should also plot your fit not only with the MMA parameters but also with the parameters optimized by Mathcad (you don't do so in your sheet.
Its interesting that the SSE value of 0,62 is the very same for every algorithm chosen (LM, conj.grad, Quasi Newton), but the values it self, especially a.rt change significantly. With pure eye not much difference can be spotted in the plot, though.
Maybe this means that you are working at the numerical limits? Not sure.
I am surprised that using the full vector of residuals in minerr
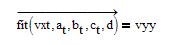
does not provide better results as it usually does. Using LM we get also 0,062, but completely different values.
Using Quasi Newton we get quite close to the MMA values but with an SSE of 0,076
Its interesting to see that argument a seems not to have much influence on the fit curve,
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thank you Werner, I see I was little confused but I can imporve and learnt a lot with your advices. Thanks
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The fact that the different algorithms give such different answers, for the same value of ERR (to 13 decimal places!) is worrying. Changing the guess value for a to 53 also makes all the answers different, but with the same value of ERR. It's also worrying that minimizing the residuals with LM gives a much bigger ERR then minimizing the SSE with LM. Lastly, changing CTOL, even to a very small number, appears to make no difference. It's as though the parameters for the fit are not independent of each other, but looking at the expression for the fitted function I cannot see why that would be the case. Is it possible that they are almost linearly related to each other in some way? Non independent parameters would also explain why the calculation of the confidence intervals gave a near singular matrix (because if the parameters are not independent, neither are the derivatives).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Get rid of the parameter c from the fit. The fit is just as good, and now all variations of minerr give the same answers. The value of ERR is still different when you minimize the residuals or SSE, but that's because of the way ERR is calculated. If you evaluate SSE, it's the same.
So the parameters are not independent (or possibly, they are algebraically independent but dependent to a very good approximation). This also explains the near singular matrix when calculating the confidence limits. Looking at the fitting function, it's certainly not obvious to me why the parameters are interdependent, but they are.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks Richard, well a and b are ks and kp for a chemical process. Maybe they are interdependent, I am not sure. But anyway, I have not the chemical-physical explanation handy, but if you say this from a mathematical point of view, it could be.





