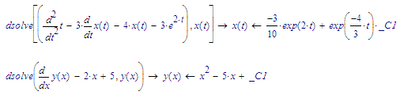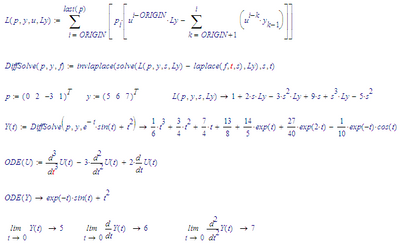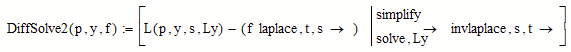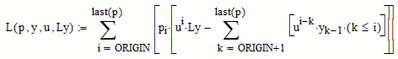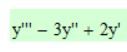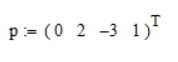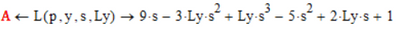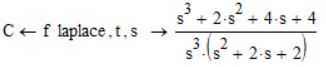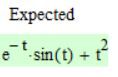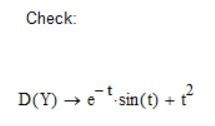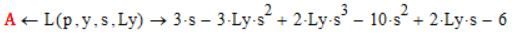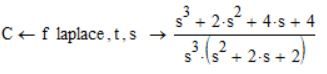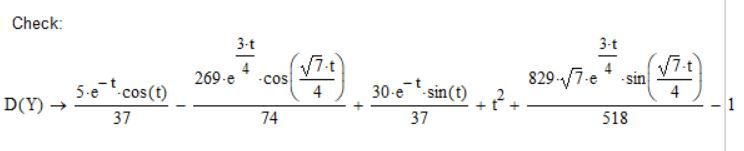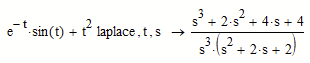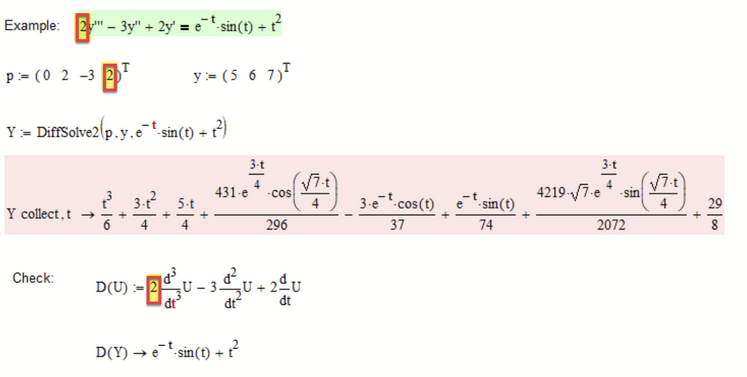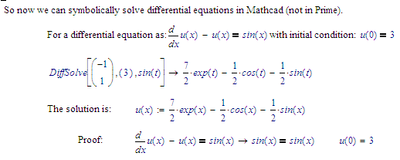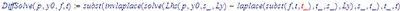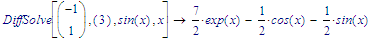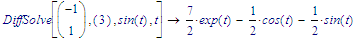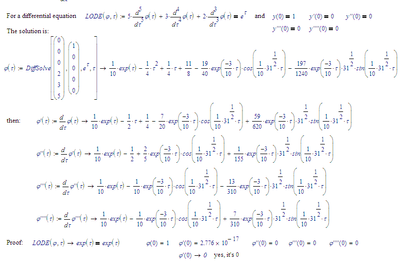Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
SYMBOLIC Differential Equation and System of Differential Equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SYMBOLIC Differential Equation and System of Differential Equation
Hello,
There is a function that can solve SYMBOLICALLY a differential equation and a system of differential equations automatically in Mathcad?
Or at least, how can I solve SYMBOLICALLY a differential equation or a system of differential equations (automatically) in Mathcad? But without using manually Laplace Transform for each term or Odesolve(-numeric/graphic), but rather something automatically...if exist...
Thank you.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Heureka! Persistence sometimes pays off!
I guess the book you referred to is "Calculus and Algebra with Mathcad" by Byrge Birkeland. There was a version of the book for Mathcad 8 from 1999 and a later version for Mathcad 2000. Not sure if the MC8 version already included that chapter (4.3.2).
Anyway, here is a modified version of the described method which also works in Mathcad 15 (it will not work in Prime). As in the original version, the independent variable must be called "t" - this is mandatory!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately Mathcad does not provide any means to solve and ODE symbolically.
Best advice would have been to use Laplace which could be automated in older Mathcad versions MC11) but not in the current ones (neither in Mathcad 15 nor in Prime).
For symbolic solutions you will have to resort to programs like Maple or Mathematica.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So...the only solution is to apply Laplace Transform manually for solving symbolically differential equations and systems of differential equations in Mathcad?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Cornel wrote:
So...the only solution is to apply Laplace Transform manually for solving symbolically differential equations and systems of differential equations in Mathcad?
Sure not the only solution, but Laplace seems to be the easiest way in many cases. But of course you could also solve the ODE(s) manually by integration and let Mathcad do the basic integration work.
Anyway, I don't know of a way to fully automatically get the symbolic solution for an ODE or a system of ODEs with Mathcad.
A long time ago I played around with the idea of writing functions to solve ODEs automatically in Mathcad using integration, but I only finished /to some part) linear first order ODEs and never took time to extend the method at least to second order ODEs (which I guess should be possible), let alone systems of ODEs.
As far as I remember, it was particularly tricky to find a way to use arbitrary names for the independent variable so as not to be set to just x or t.
In case you are interested and like to work along I attach the file. The comments mostly are in German but I guess you'll get the idea how to use the functions.
BTW - as the functions require symbolic evaluation inside of a program, they will not work in Prime any more.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I found in a book this way (function) of the implementation of Laplace Transform for a differential equation, but I encountered some errors...and I don't know how to fix them for this moment.
If you have any idea of how can resolve these issues...are welcome.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The math notation y^(i) for the i-th derivative is not understood by Mathcad
Mathcad (at least the version we use) does not understand a function "solve" or a function "laplace".
In Mathcad 15 "solve" and "laplace" are keywords for symbolic evaluation but not stand alone functions.
What your book shows may work in Mathcad 11 (Luc could verify). You remember that I wrote in my fist answer here that solving an ODE via laplace could be automated in MC11 (which uses Maple for symbolics), but not in later versions like MC14 or MC15, which use a different symbolic engine (muPad).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The very first error that your file shows is due to you. If you follow the notation of professor Birkeland carefully, you'll see that he writes an equation (using =), not a definition (using :=).
Such an equation can be, and often is, used to describe a mathematical concept in a notation that escapes Mathcad's error checking.
The book was written for Mathcad 2000, a predecessor of Mathcad 15. With the change of symbolic processor going from Maple (unitil Mathcad 13) to Mupad (as of Mathcad 14), many symbolic possibilities were broken, a few were improved.
I'll see if I can make Birkeland's functions work in Mathcad 11.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Given the right version of Mathcad (11), and some tweaking:
But all this is unsupported.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which means that you use Maple features not available in current Mathcad or Prime and which were never supposed to work in Mathcad the way you use them 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Heureka! Persistence sometimes pays off!
I guess the book you referred to is "Calculus and Algebra with Mathcad" by Byrge Birkeland. There was a version of the book for Mathcad 8 from 1999 and a later version for Mathcad 2000. Not sure if the MC8 version already included that chapter (4.3.2).
Anyway, here is a modified version of the described method which also works in Mathcad 15 (it will not work in Prime). As in the original version, the independent variable must be called "t" - this is mandatory!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great!
In Mathcad 11 the construct with k<=i fails. As soon as I put that in, the function L forgets about the initial conditions, they're all set to 0.
Since its use is to limit k from going above i, this can also be accomplished by the upper limit of the inner summation. I also observed that the L function is not ORIGIN aware.
It appears that I can compact the DiffSolve function to a oneliner.
The result is:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The one liner sure is possible only in MC11 but not in MC15.
The construct with *(k<=i) is necessary in MC15. I am not sure why, but the symbolic in MC15 seems not to like the "i" as an upper limit of the second sum.
The error message when trying to symbolically evaluating L(..) is "assumption impossible (property::Null)" ????
Otherwise your implementation would sure be more elegant and preferable. And yes, I agree that L should be written ORIGIN-aware 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
BTW, here is the one-liner which works in MC15, but its ugly and confusing looking
and because of the various symbolic evaluations it "grows" and always shows the intermediate results of the last example it was used for:
I would stay with the four-liner I posted before, using an ORIGIN-aware function L, of course
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hm Werner,
did you check your L function with an ORIGIN other than 0?
I think it should go wrong. The power of u, just before Ly, needs to start at 0, independently of the ORIGIN, so you should subtract ORIGIN from i there...
Then, you say this does not work in Prime.... have you tried? (What limits Prime from doing this?)
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are absolutely correct - what I showed in the pic would not work OK with an ORIGIN other than 0. u has to be raised to the power of i-ORIGIN and not just to the power of i.
No, I didn't give it a try in Prime because I know that PTC has limited the use of symbolic evaluation there.
You probably know that solve block can't evaluated symbolically anymore in Prime.
What would make my sheet fail in Prime is the fact, that Prime does not allow symbolic evaluations inside of a program and my approach heavily relies on doing so (three times, because the first evaluation of L(..) must not necessarily be done).
Symbolic evaluations inside of a program are a bit tricky in real Mathcad, too. We need to type the expression with the symbolic evaluation at some space outside of the program and have to copy and paste that expression to the program we are about to write. Trying to add a symbolic eval directly when writing a program would result in a symbolic eval of the whole program, which would not do the desired job.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I understand that the relationship for A:
is deduced from ODE:
But how do you deduced/reached the relationship for C: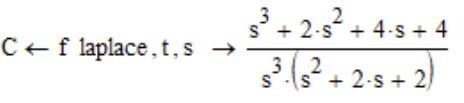
Case 1:
Case 2:
Why the result is different?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
C is the laplace transformed of the source term function f
I simply splitted Birkelands second program line into two, because Mathcad 15 does not offer a laplace function, only symbolic evaluation using the laplace keyword.
As shown in my last answer its possible to create a one-line function in Mathcad 15, too, but the multi-line version is much more clearer, I guess.
According your case 2:
If you change the coefficient of the third derivative, you also have to change it in the "check-function" 😧
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A, ok.
Thank you very much for your response and time in resolving this question.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Cornel wrote:
A, ok.
Thank you very much for your response and time in resolving this question.
Thank you for pointing me to Prof. Birkelands approach which enabled me to create a version working for Mathcad 15.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What I wanted to achieve is to put an ODE into a function and that function to give me as a result the solution of that ODE...and not to make even the transformation from t domain to s domain manually and then somehow to take inverse Laplace of that result. (if it is possible such a thing:))
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Cornel wrote:
What I wanted to achieve is to put an ODE into a function and that function to give me as a result the solution of that ODE...and not to make even the transformation from t domain to s domain manually and then somehow to take inverse Laplace of that result. (if it is possible such a thing:))
Obviously you studied the file not long enough because it offers exactly what you are asking for!
You put the ODE into the function DiffSolve (by providing a coefficient vector, a vector with the initial conditions and the forcing function) and when you evaluate DiffSolve symbolically you get the symbolic solution. No need to manually make any transformations, thanks to Prof. Birkeland.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, it is true...for about one day I looked in Professor Birkeland's book.
If I will have any more questions about ODE I will post them.
Again, thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is possible to extend the function described by you not just for a single differential equation but to a system of differential equations?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Cornel wrote:
It is possible to extend the function described by you not just for a single differential equation but to a system of differential equations?
With some work and experimenting and putting some time into it, I guess it might be possible - not sure, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now the next challenge is to:
1. Lift the limitation that the independent variable must be 't'.
2. Allow the function to accept a more natural formulation of the differential equation.
Anybody?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
#1 is tricky, but I guess it could be done. See the sheet about simple first order ODEs I posted somewhere in this thread
#2 seems kind of a mission impossible to me, but I'd like to be taught better.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You mean DGL10.xmcdz?
That file is hardly readable for me. Seems like a lot of pictures are left out.
Anyway, Number 1 is solved (for Mathcad 11), using a symbolic substitute function originally from Tom Gutman (in his file xx(1186) he named it Rep), which I adapted to be a little more versatile:
With that, the symbol for the independent variable in f is changed to t_, and finally in the result t_ is changed back to the independent variable name supplied as an argument to DiffSolve:
This allows me to:
or
or even:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
DGL10 doesn't fully run in Mathcad 11. Hope there's no need for it to.
I've tried my best to convert my LODEsolver to meet Mathcad 15's requirements.
So now it doesn't run in Mathcad 11, but... Does it run in mathcad 15?
If not: what is needed to make it run?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately the sheet does not work in MC15.
The first error after manual calculation of the sheet is in "subst"
and when clicking that region, the symbolic evals of the transferred function is expanded, messing up the sheet.
The error is "This function refers to itself inconsistently".
A second error I spotted here