Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Shear Force in the Diagramm is not sucessful displayed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Shear Force in the Diagramm is not sucessful displayed
Hello,
I'm trying to plot a Shear Force-Diagramm, but it fails at its graphical representation.
Normally it should displayed like this:

...but it is like this (see attachment):
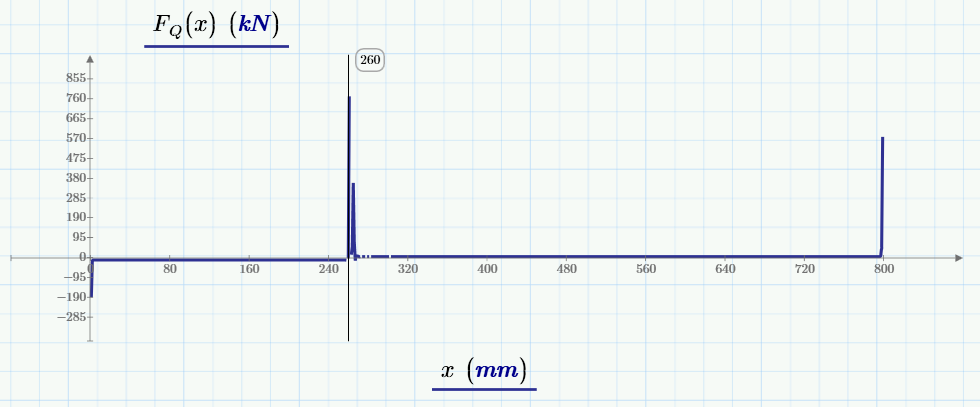
Can somebody help me?
Thanks, Volker
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The sheet calculates the end reactions Fa and Fb, whether correctly or not I haven't tried to determine.
His solution method is to solve the differential equation for deflection from both sides, which is valid (and impressive.) He then creates a deflection function by patching these two solutions together and takes the double derivative to get moment; again correctly. To get shear he takes the derivative of moment, which works everywhere except at the ends of the beam and where the two solutions patch together, where the derivative fluctuates wildly.
Mathcad scales the shear graph to show all of it's reported values, so it shows the wildly incorrect fluctuations. If we rescale the shear graph to reasonable limits and ignore the wild excursions it should make sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can you please post more screenshots or a PDF of your worksheet? Many of us do not have Prime 3.1 installed, so we cannot open your file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Something is wrong, even here ...
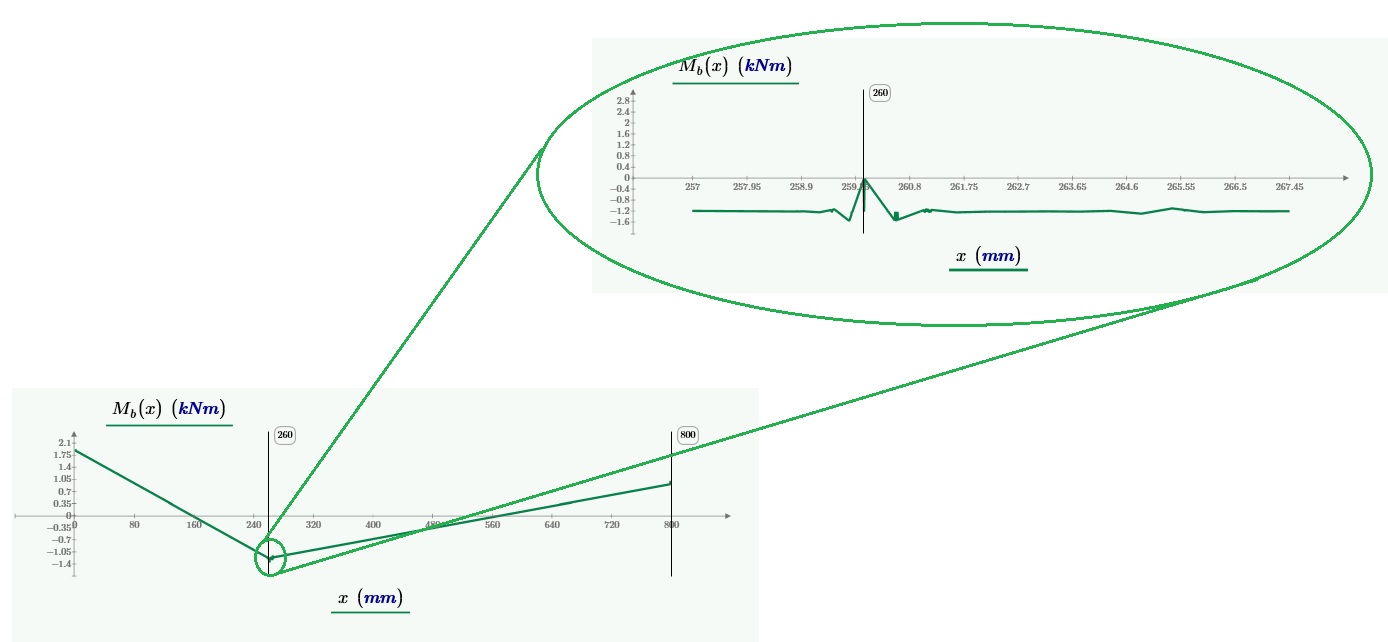
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your plot of shear force (F_Q) is seeing large oscillations because there are discontinuities in moment that aren't easily seen in the graph. Try limiting your F_Q graph to ±20 kN, see the result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
limiting the F_Q diagramm with +-20kN, you will get following result:

you can see the two reaktion-forces as a straight line, but the discontinuities still exist.
Trying to change the steps from 1mm to 10mm for the x-axis leads to:
![]()
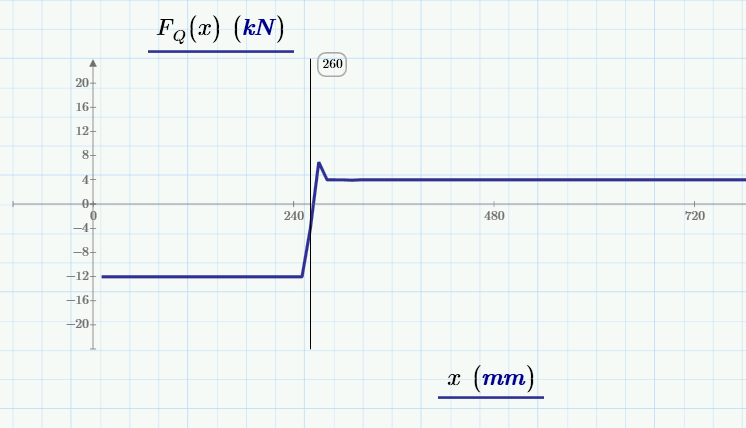
I guess, the discontinuities depends only on the derivation of the bending moment and shear force.
Much better is the definition of the shear force without derivations.
see attached PDF.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
If the case in question concerned a beam resting at the ends and subjected to the only force F, the reactions at the supports should simply be: Ra = (1-k) * F + p / 2, Rb = k * F + p / 2 where p is the weight of the same beam (negligible) and k = a / L. In this case the diagram of stress would be the one shown above. But In the present case, there are two other forces Fa and Fb proportional to F, each attached to the ends of the beam. In fact, if F = 2kN is: Fa = 12.03kN and Fb = 3.97kN.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The sheet calculates the end reactions Fa and Fb, whether correctly or not I haven't tried to determine.
His solution method is to solve the differential equation for deflection from both sides, which is valid (and impressive.) He then creates a deflection function by patching these two solutions together and takes the double derivative to get moment; again correctly. To get shear he takes the derivative of moment, which works everywhere except at the ends of the beam and where the two solutions patch together, where the derivative fluctuates wildly.
Mathcad scales the shear graph to show all of it's reported values, so it shows the wildly incorrect fluctuations. If we rescale the shear graph to reasonable limits and ignore the wild excursions it should make sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Fa and Fb are correctly.
you are right, it depends on the derivative fluctuates wildly.
Thanks for the confirmation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The force F was defined in two different positions of my worksheet, and this has a little puzzled me since the results did not change ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Since you have expressions for end reactions, you could solve this problem "upside down."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
your sheet looks very interesting, btw the plotting of the deflection takes a lots of time to be displayed.
I want to share my Original Worksheet with you all, this worksheet is about analytical solution of a beam with two fixed bearings and one Load.
I wanted to solve this problem with the solve-blocks, but there was a problem to calculate Fa,Fb,Ma,Mb because they are unknown.
Have Fun ![]()
Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The deflection calculation requires integrating three times:
1) Integrate shear to get moment.
2) Integrate moment to get slope.
3) Integrate slope to get deflection.
The graph has to do that for each point. A potential work-around is to fit high-order polynomials to each step (or at least to the slope function) This will shorten the integration time, although at the expense of accuracy.
I was just showing that if you knew the end reactions you could do the problem the way we were taught in school. (How you got those values is still a mystery to me!.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't read Prime 3.1 files. Your first attached pdf has four equations for the end reactions:
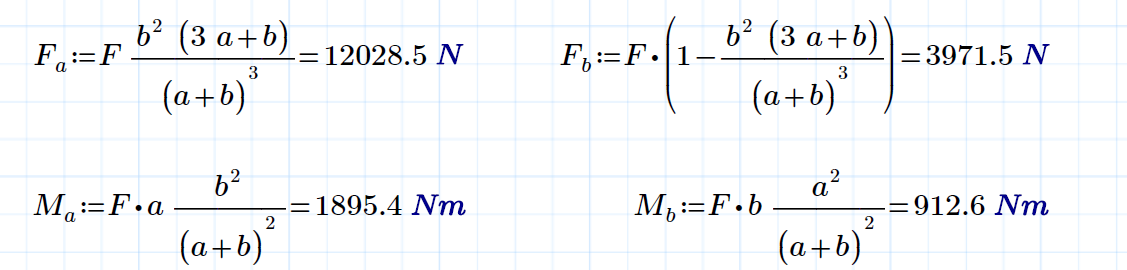
I haven't located a source for those (haven't looked.) This is the source of my comments,
"The sheet calculates the end reactions Fa and Fb, whether correctly or not I haven't tried to determine." and
"(How you got those values is still a mystery to me!.)"
I meant no disrespect, simply that you had equations for the end reactions that I'm not familiar with.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello
It seems to me that Fb should be (F.a ^ 2).(3.b + a)) /(a+b) ^ 3
Sorry for writing
Kind regards.
Denis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I expect you're right, but it's also true that Fb =F-Fa, which is what's in the equation. I suspect a little manipulation could show the equality.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
My solution for Fa,Fb,Ma,Mb you posted I want you to show you my derivation for that 4-static quantities.
At first you have to find the Integration-constants with the geometrical relationships, shown at the highlighted equations at Page 1

The next step will be to set the found constants into yl(x) and yr(x): Then you will get this equations of the deflection
(two functions for the left and the right side of the beam):

Now we had to set up a system of equations respective the geometrical relationships at the point "a" where the shear force "F" is (see page 2):
1. The deflection at point "a" from yl(a) must be equal to yr(a): yl(a)=yr(a)
2. For the slope it has to be equal too for both functions: y'l(a)=y'r(a)
(look at the deflection-diagramm at page 4)
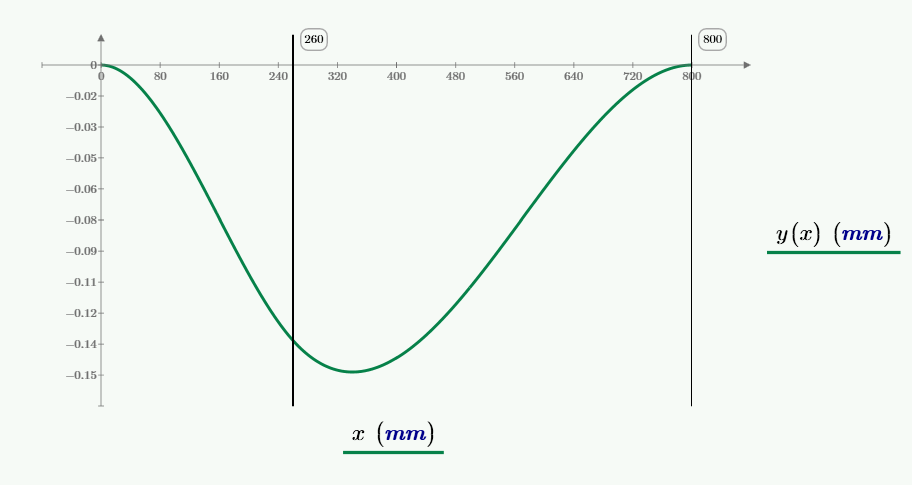

If evaluated, you'll get the solutions for Fa,Fb,Ma and Mb:

regards, Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very nice!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think Mathcad can handle the fourth derivative boundary problem directly (Might want to try "sbval" function, and the old way of solving boundary value problems.
The other way would be to recognize that y has to be a combination of functions whose fourth derivative and third derivatives have to equate to zero at the ends of the beam. (sine, cosine, hyperbolics, etc.) Use the end constraints to knock out terms, then solve for coefficients. . .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Volker
You wrote:
Why does the solver not work properly with Units?
Is it a MathCad-Problem or whatever?
The beam is fixed at it's ends an the Load is a constant stretching load.
Your right, Prime is able to solve this boundaryvalue-problem without units, but I was not able to solve this problem with units, too. If you have a look at the examples I posted today, you can see, that Prime still is less capable than Mathcad 15, when solving numerical problems. So it is probably a Prime-problem.
But even with Mathcad 15 I avoid the methode you used. With noncontinuous functions odesolve often did not converge. I prefer to go over intial-value-problems and tweaking the initial values with a solve-block.
Regards
Ueli
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attached you will find two files in Mathcad 15 and Prime 3.1 with nummerical calculations of loaded beams.
In Prime the unit-handling is much better, but the nummerical power of Prime is still poor: In the example given as pdf, too, I had to use the result from 15 to chose initial values close to the result, to bring Prime to converge.
At the end of these pdf's you see, that 15 performs better, when calculating the shearforce by differentiating y(x), but you still observe oszillations.
Regards
Ueli






