Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Simple equation - result far too complex and wrong
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Simple equation - result far too complex and wrong
Whats wrong with Mathcad or with that simple equation - why is Mathcad not able to find the two solutions 0 and 3 ??

Needless to say that the given "solution" 3.34 is wrong!
If variable x is restricted to be a positive (or zero) real number the "solution" is shown:
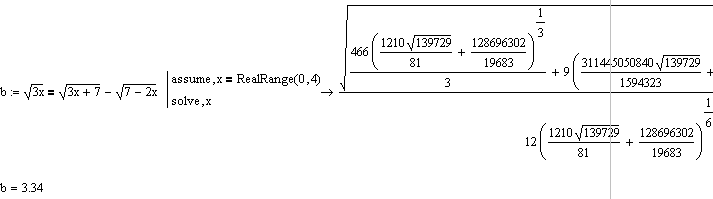
Is this a bug?
I am using Mathcad 14 (M030).
Is Mathcad 15 doing better on the job?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
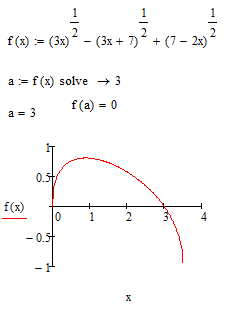
Mathcad 15 (MuPAD not Maple - in Maple I have two roots 0 and 3)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Square both sides and Mathcad immediately finds the two solutions:
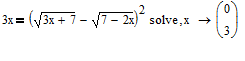
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maple is Maple:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
MC_User wrote:
...Is Mathcad 15 doing better on the job?
In Mathcad 15 M010 obtained the same result as shown in your screenshot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is this a bug?
Sure, and an interesting one, indeed.
Does anybody know, which symbolic engine ist behind Mathcad Prime 2.0? Is it still MuPad or is it something else?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes it is MuPad.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guest2 wrote:
...Does anybody know, which symbolic engine ist behind Mathcad Prime 2.0? Is it still MuPad or is it something else?
No. It still MuPad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The value of x can be complex (i.e. have an imaginary part), and each of the three square root terms can be positive or negative in the general case, so that give 4 different potential pairings (after dividing through an common minus sign).
MuPad is of German origin and takes a precise approach to problem solving so does consider all those factors. Maple embeds some common solutions as a short cut, which are actually wrong (incomplete) in the general case.
It is usually necessary to add the unstated assumptions of being real, and positive square root (which is hard) to get the simple answer you are expecting.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The answer 3.34 is still wrong though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
The answer 3.34 is still wrong though.
It's near enough for pit work though (phrase learnt when working in the Durham coalfields;-)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
The answer 3.34 is still wrong though.
Yes, and as a symbolic solution one should no accept approximations. the exact expression which simplyfies to 3.34 is shown partially in a screenshot in the original posting and I can duplicate it here - teriffic.
Wonder what algorithm MuPad is using so it lands a an third order equation.





