Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Sinuswave with randomly variable frequency
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sinuswave with randomly variable frequency
Hi everyone,
I seem to need the help of the forum often lately... ![]()
I need for test purposes to generate a sinus-wave with randomly varying frequency (and possibly also amplitude, but that is the lesser problem). Something like an oscillator whose frequency is not perfectly stable. Or an oscillator whose frequency setting adjustment button would be slightly turned right and left randomly by a small amount. Something like this:
I attached my solution, but I am not happy with it at all. Obviously the "randomness" becomes higher and higher with the time, and for the same reason there are unwished jumps in the later part of the simulated signal.
I understand that the problem is the time variable "t" in the equation A*sin(2*pi*f(t)*t) .
But at the moment I can find no good simple way to correct the behaviour.
Maybe I am missing something obvious ... I will be grateful for any hint.
Best regards
Claudio
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
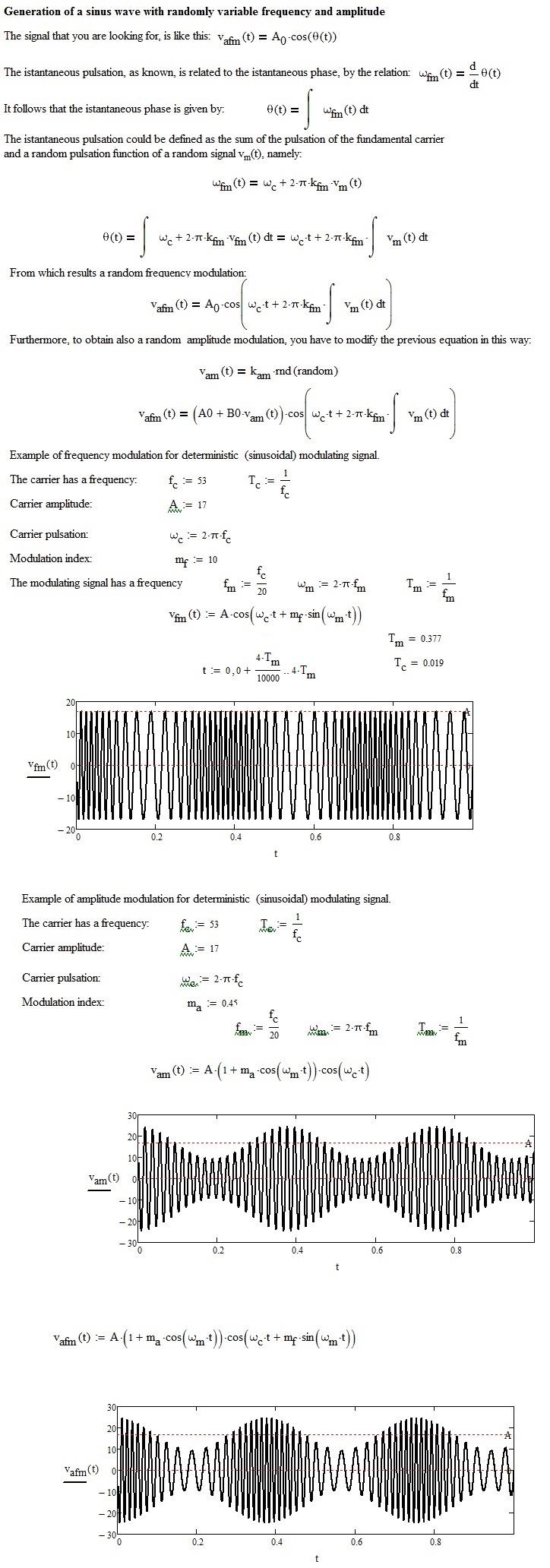
Hi Claudio,
in what follows, you should substitute the deterministic signal with a random one:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Claudio,
in what follows, you should substitute the deterministic signal with a random one:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think your problem lies in "phase jitter" for want of a better term. You have a function that depends on time and varies frequency. The further you are from time zero, the larger the "error" in amplitude is because sin(f*t) is changing with frequency as well as time.
Attached is a file that looks at that, then develops a vector signal based on varying the time step rather than the frequency. You can see and play with the differences.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The randomness should be in the phase, not the frequency. Then it will not scale with time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi everyone, and a big thank you to all contributors. I appreciate, as always, the time and effort that you put into answering.
The approach that worked best for me is the one of F.M. , but also the others are very interesting hints. I am posting here my complete worksheet, as a contribution for future to the community.
I changed a little the naming convention and the scaling, because I wanted the "randomness" to be adimensional (so random=30% should mean the frequency can vary around +-30% of the carrier frequency, and the same for the amplitude). also added a small function to try to "measure" the instantaneous frequency, to check if the method was working; this function is not perfect but it provides an indication.
Again, thanks a lot! this forum is a real help.
Best regards
Claudio





