- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solution extremely sensitive to guess value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solution extremely sensitive to guess value
Hello All
I am doing a minimization of the torque in mathcad and the solution that i am getting is heavily influenced by the guess values and each time I change the guess value a,b etc even by a small amount,it gives me a different answer. I really am not sure why it is doing that and also how am I going to rectify it.I have enclosed my worksheet . Any help would be greatly appreciated
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
Hello werner
I would be very grateful if you could tell me how exactly do I implement the function check on TT?. I thought about it today but dont know how to implement it. I will check if I can find additional constraints so that i dont have to do the function check on TT
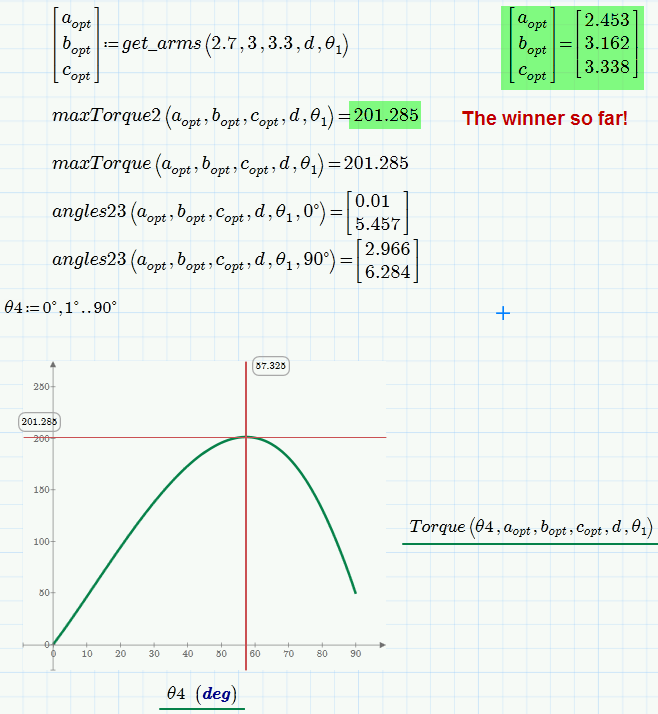
I tried a different approach in the attached sheet. It is not assumed here that the max torque will appear at 60° but is correctly calculated using a solve block. This significantly increases calculation time in the final solve block.
I also tried to implement the aforementioned quick hack to avoid invalid solutions but I still guess that checking the math of the geometry and incuding meaningful constraints would be the better approach.
Unfortunately the end result of my efforts is a bit unsatisfactory as we still get invalid result in some cases and the solve block is quite sensible wrt the guess values.
Nevertheless I think the results should be useable.
You may play around with the constraint 2<a<5 and of course with the guess values.
I had assumed that the values are valid if I get a solution for theta2 and theta3 for theta4=0 and theta4=90°. I once came up with a combination of arm lengths which will be fail only for theta4 in approx. 7° to 20°. This case would not be cought by my routine and I can't remember what the values for a,b and c were.
Regrettably I am lacking the time to further investigate but maybe you or someone else here can come up with something a bit more stable and less sensible.
Good luck!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your objective function seems to be very flat. A lot of combination of parameters yield results which are very close.
What counts is the value of the objective function when fed with the optimized arguments. To Mathcads numeric it does not make much difference if the value of T is -1*10^-31 or +2*10-25. Even decreasing the values of TOL and CTOL doesn't change that much.
You also get slightly different result if you don't change anything but simply recalculate the worksheet (Ctrl-F9). .-)
So change your guesses and watch the result of T(..) - its always close around zero, no matter how much the absolute values of the arguments may be. If thats an issue you might consider scaling your function (multiply by 10^20 or higher, for example).
I have omitted the constraint for d (you don't solve for it) and have added a guess for m (you solve for it) and als added a as argument of T as it seems you want to solve for it, too. You might do the same with theta1 if thats something you wanted to achieve.
BTW, If m should be dependent on c you would have to write it that way. I haven't done so because its not clear to me what your goal is.
You also have to be aware that the constraints are soft constraints. You see that in the picture looking at the result of theta4 which is negative. If a constraint is very important for you you may consider "weighting" it by multiplying it with a large number. So you may write something like
![]()
but of course then other constraints might get out of range. Mathcad just tries to get a good overall fit regarding the minimization of your objective function and the given constraints. So doubling a constraints as I had done in another thread of yours can change the result. The effect looks not always logical to us.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner
Thank you so much for getting back to me. Actually my objective is to adjust a and c to minimize the maximum torque(T) that I have got in mathcad worksheet, mathcadtoggleprog2 which I have enclosed.The T which is the objective function was obtained after solving the system of equations in the worksheet mathcadtoggleprog2.When I attempt to minimize in the worksheet mathcadoptimizationtrial_WE_1, I am getting an erroneous answer a=0 which is basically an arm length.I really dont know why its doing that. i have also enclosed the worsheet where I did the minimization based on the changes you suggested.Any help would be greatly appreciated
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
Hello Werner
Thank you so much for getting back to me. Actually my objective is to adjust a and c to minimize the maximum torque(T) that I have got
So you don't want to change/optimize the three theta angles (2,3,4)? Just a and c?
When I attempt to minimize in the worksheet mathcadoptimizationtrial_WE_1, I am getting an erroneous answer a=0 which is basically an arm length.I really dont know why its doing that.
Because with the values (a, c, and the specific angles) minimize() comes up with, you get torque T is zero and that seems to be a valid minimium.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
actually torque is a function of a,c and the three angles.The three angles(2,3,4),a and c are related by the first 2 constraints.But my objective is to get a value of a and c(basically are the arm lengths) which will minimize the maximum value of torque
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
actually torque is a function of a,c and the three angles.The three angles(2,3,4),a and c are related by the first 2 constraints.But my objective is to get a value of a and c(basically are the arm lengths) which will minimize the maximum value of torque
Two constraints but three angles (and a and c) for Matcad to play with - a lot of degrees of freedom, so why should Mathcad not set theta4 to 0?
You wrote that max torque is achieved for theta4=60°. So you can omit theta4 from the argument list. What about theta2 and theta3? Is there also a fix value for those angles which yield the max torque? Or can you make the angles which yield the max torqued ependent on a and c. Then you would have to setup the minimize() solve block completey different.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the problem is theta 2 and theta 3 depends on a,b and c based on the contraints acos(theta2)+bcos(theta3).....=0
and asin(theta2)+bsin(theta3)...=0.If a and c are changed theta 2 and theta 3 also changes.So we cannot fix theta2 and theta3 .but I have added that a,b and c should be positive numbers as a constraint.I would be grateful if you could give me some tips on how to set up the solve block if that is the situation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Take a look if the attached comes closer to what you want.
I made a torque function (TT) which is dependent on a and c only. theta4 is 60° and theta2 and theta 3 are calculated from your two equations in a solve block which is turned into a function (angles).
I get a minimal value of ca. 102 for torque - is that reasonable?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you so much Werner. The torque value seems reasonable
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello werner
I jus realized today that although the torque values are acceptable, the values of a and b does not satisfy the constraint acos(theta2)+bcos(theta3)....=0 and asin(theta2)+bsin(theta3)...=0 for the entire range from theta 4=0 to theta 4=90 and it satisfies the connstraint only at theta4=60 and thats expected as we minimized the equation at theta4=60.But I would like to find an a and b that satisies the constraints for the entire range ie from theta4=0 to theta4=90.I would be very grateful if you could tell me how do I proceed with such a situation?.- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
Hello werner
I jus realized today that although the torque values are acceptable, the values of a and b does not satisfy the constraint acos(theta2)+bcos(theta3)....=0 and asin(theta2)+bsin(theta3)...=0 for the entire range from theta 4=0 to theta 4=90 and it satisfies the connstraint only at theta4=60 and thats expected as we minimized the equation at theta4=60.But I would like to find an a and b that satisies the constraints for the entire range ie from theta4=0 to theta4=90.I would be very grateful if you could tell me how do I proceed with such a situation?.
I am not sure if I understand what you want to achieve.
Your two equations depend on four lengths (a,b,c,d) and four angles (theta1..4). b, d are constants. a and c are calculated per minimization and theta 2 and theta3 are calculated given a and c and constant values for theta1 and theta4. So its clear that the equations can't be satisfied when you change only theta4.
Also torque depends on the constant w, a, c and theta 2..4. So if you change theta4 torque is not minimized any more.
You may think over which variables should be constant and which vary and how all those variables should depend on each other, As an example my function "angles()" depends on theta4 being a constant value.
If you vary theta4 you will get different lengths a and c for different values of theta4.
And what about theta1? Should it also vary?
I am not sure what kind of minimization you have in mind now.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Helo Werner
Thank you for the reply.My objective is to minimize the torque curve that I got in the worksheet mathcadtoggleprog2 that i have enclosed earlier.In that worksheet it is seen that the torque is maximum at theta4=60 degrees.the problem is if we minimize only for theta4=60 the value of a and b to get the minimized torque will satisfy the 2 constraints acos(theta2)+bcos(theta3...=0 and asin(theta2)+bsin(theta3)...=0 only at theta4=60. Basically these constraints are geometrical constraints to ensure that it remains a 4 bar linkage for that range of angles from theta4=0 to theta4=90.The torque curve that I got in the worksheet mathcadtoggleprog2 was the torques from theta4=0 to theta4=90.These linkages move through the range from theta4=0-90.So the a and c values that I get from the minimization should ensure that it remains a 4 bar linkage(basically satisfies the 2 constraints in the range theta4=0 - theta4=90)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess when theta4 changes and a,b,c,d remain constant, the other angles would have to change to satisfy the two equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello werner
a,b,c and d are arm lengths and theta1,theta2.theta3 and theta4 are the angles. In this case actually only w,d and theta1 are fixed. So if theta4 changes every other dimension other than whats fixed has to adjust itself so that it satisfies the 2 constraints.so my objective is to get an optmized configuration (basically value of arm lengths a and c) which will help me minimize the torque.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
Hello werner
a,b,c and d are arm lengths and theta1,theta2.theta3 and theta4 are the angles. In this case actually only w,d and theta1 are fixed. So if theta4 changes every other dimension other than whats fixed has to adjust itself so that it satisfies the 2 constraints.so my objective is to get an optmized configuration (basically value of arm lengths a and c) which will help me minimize the torque.
The question is what "optimized configuration" and "minimized torque" are defined as. I guess in a given configuration the arm length are supposed to be constant throughout but the angles are allowed to changed as long as your two equations are satified. As I see it you will have to solve for b, too, as its not a constant.
But now I don't understand what you told about "the values of a and b does not satisfy the constraints ... for the entire range from theta 4=0 to theta 4=90". I guess they will, but of course theta2 and theta3 will change when you change theta4. Or am I missing the point?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner
I have enclosed a pdf document to show the geometry to explain the angles and lengths.The angle that linkage with length a is inclined to horizontal is theta2....the angles that linkage with length b in inclined to horizonal is theta3,the angle of linkage with length c is theta4 and the angle of linkage with length d is theta4. So basically if theta 4 changes,every other parameter changes.In this case only w(weight), d and theta1 are fixed. so basically i need values for a,b and c which will help me minimize the torque curve that i got in the worksheet mathcadtoggleprog2 .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the worksheet mathcadtogglepro2, i have used specific values of a,b,c and d to generate the torque curve and the maximum is at theta4=60 and the torque is around 231. But this may not be the optimum configuration .What i need is values of a,b and c to get a torque which is less than 231.But in the process it should also satisfy the 2 geometric constraints as this 4 bar chain moves from theta4-0 to theta4=90 and it should remain a 4 bar chain for 90- degree rotation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"But now I don't understand what you told about "the values of a and b does not satisfy the constraints ... for the entire range from theta 4=0 to theta 4=90""
The optimized value that you got in the worksheet you enclosed a=1.237,b=3.027,c=3.506 and d=3.144 satisfies the 2 geometric constraints only at theta4=60 but it does not satify the geometric constraints when theta 4 is changed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
"But now I don't understand what you told about "the values of a and b does not satisfy the constraints ... for the entire range from theta 4=0 to theta 4=90""
The optimized value that you got in the worksheet you enclosed a=1.237,b=3.027,c=3.506 and d=3.144 satisfies the 2 geometric constraints only at theta4=60 but it does not satify the geometric constraints when theta 4 is changed
That depends on theta2 and theta3! They will have to be changed, too, if you change theta4.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is there is no solution for theta 2 and theta 3 which satisfies both constraints for theta4 from 0-90deg for a=1.237,b=3.027,c=3.506 and d=3.144. For example when theta 4=90,the given values dont satisfy the 2 constaints acos(theta2)+bcos(theta3)...=0 and asin(theta2)+bsin(theta3)....=0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
The problem is there is no solution for theta 2 and theta 3 which satisfies both constraints for theta4 from 0-90deg for a=1.237,b=3.027,c=3.506 and d=3.144. For example when theta 4=90,the given values dont satisfy the 2 constaints acos(theta2)+bcos(theta3)...=0 and asin(theta2)+bsin(theta3)....=0
I see! And from your drawing its easily seen that the arm c would not be able to move up to 90 degree because arm a is far too short to accomodate that. So you would need additional constraints for a and c (and possibly b, too) to work out and put then in the solve block.
While looking at your drawing I wonder if your two constraint equation are correct. Can you explain that term atan(0.56/sqrt(c^2+0.56^2))? Why is this angle added to theta4?
BTW, the maximum torque is usually NOT exactly at 60 degree and the positions varies depending on the arm lenghts!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
actually the constraint equations are correct. I actually made a mistake in the diagram I sent you and the angle that i have shown as theta4 is actually theta4+atan(..).i have enclosed the new figure.The only constraints for a,b and c are that they should be greater than 0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
actually the constraint equations are correct. I actually made a mistake in the diagram I sent you and the angle that i have shown as theta4 is actually theta4+atan(..).i have enclosed the new figure.The only constraints for a,b and c are that they should be greater than 0.
No, and thats the problem. There are more constraints you have to find out. As you have seen you don't get a solution for the angles with certains combinations of the arm lengths. This is due to the fact that your four-bar linkage will lock if e.g. a is too small. c would then not be able to move up to full 90° or down to 0°.
Another method would be that the function TT checks if you get a solution for theta4=0 and 90° and if not, it would yield a rather big result so that it will fall out of minimization. Quick and dirty but it may work.
Better of course you check your geometry and find some constraints for a, b and c which would guarantee that c can move in the range of 0 to 90 °.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello werner
I would be very grateful if you could tell me how exactly do I implement the function check on TT?. I thought about it today but dont know how to implement it. I will check if I can find additional constraints so that i dont have to do the function check on TT
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
Hello werner
I would be very grateful if you could tell me how exactly do I implement the function check on TT?. I thought about it today but dont know how to implement it. I will check if I can find additional constraints so that i dont have to do the function check on TT
I tried a different approach in the attached sheet. It is not assumed here that the max torque will appear at 60° but is correctly calculated using a solve block. This significantly increases calculation time in the final solve block.
I also tried to implement the aforementioned quick hack to avoid invalid solutions but I still guess that checking the math of the geometry and incuding meaningful constraints would be the better approach.
Unfortunately the end result of my efforts is a bit unsatisfactory as we still get invalid result in some cases and the solve block is quite sensible wrt the guess values.
Nevertheless I think the results should be useable.
You may play around with the constraint 2<a<5 and of course with the guess values.
I had assumed that the values are valid if I get a solution for theta2 and theta3 for theta4=0 and theta4=90°. I once came up with a combination of arm lengths which will be fail only for theta4 in approx. 7° to 20°. This case would not be cought by my routine and I can't remember what the values for a,b and c were.
Regrettably I am lacking the time to further investigate but maybe you or someone else here can come up with something a bit more stable and less sensible.
Good luck!


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thank you so much Werner for all your help. I will go through it and try working on this
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vishniu Gopalakrishnan wrote:
thank you so much Werner for all your help. I will go through it and try working on this
You are welcome!
Let us know if it has helped and you had success.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello werner
this is exactly what I wanted and I was able to get a combination of guess values to bring the torques down to 197. Thank you so much for that
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So we have a new competition 😉
Here you have a set which yields a torque of 183.
But its incredible how sensible the system is. I won't trust the results without double checking!
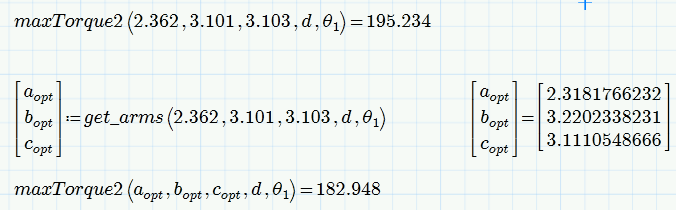
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I had checked that set of values and it gives you a very unrealistic answer for the angles when theta4 is 90 degrees.I got theta 2 and theta 3 as -34 and -28 radians.So i discarded it





