Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solution to a task from IMO 1988 - calculation of examples
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solution to a task from IMO 1988 - calculation of examples
In 1988, the International Mathematical Olympiad was given the task B3: If for integers x and y the term (x^2+y^2)/(1+x*y) is a natural number N, then N is a square number. The solution does not require advanced mathematics, but is very challenging. I have attached a German language file MC14. I saved myself a translation into English because the solution should be self-explanatory with little translation help. Examples are included at the end of the file.
In the solution, a recursion is constructed based on starting values that have yet to be found. And that's my problem. My programming knowledge is not sufficient to find starting values and apply the recursion described in the solution - I therefore ask for help.
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you. The calculation also shows the canceling recursion according to "infinite descent". This is very helpful for understanding the solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
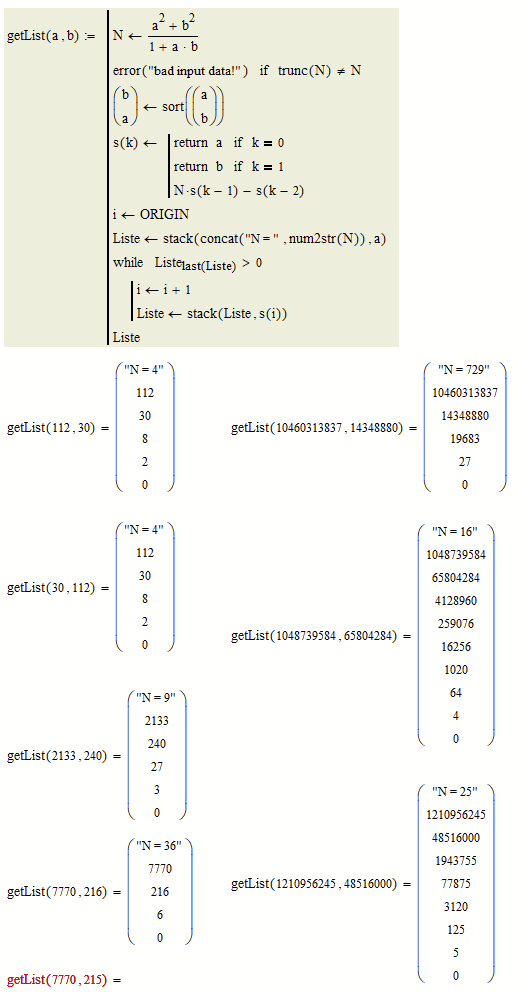
Die Erstellung der Liste geht natürlich einfacher ohne Verwendung der lokal definierten rekursiven Funktion s(k).
ZB
oder auch
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mit solch effektiven Programmiertechniken bin ich überfordert. Ich kann sie nur halbwegs verstehend lesen. Inzwischen habe ich die ursprüngliche Aufgabe (1) aus der angehängten Datei als quadratische diophantische Gleichung gelöst. Es ergeben sich lineare Rekursionen, die zu einem Bildungsgesetz führen. In derive habe ich dann damit die Langzahlarithmetik erfolgreich angewendet. Schüler und Studenten aus dem Bekanntenbereich werden sich bestimmt freuen. Also nochmals vielen Dank für Ihre Hilfe.