Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve-Block-Solution: non linear EQN-System
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve-Block-Solution: non linear EQN-System
Hi!
Maybe today it is much too hot and I have drunk too little water and coffee, but i can't find a stable solution for a defined problem:
I have to solve a mechanical problem (dimensioning steel cables) with the solve block including 18 equations with 18 unknowns:
It is required that the length change, the number of threads and all forces, etc. are calculated with the solver.
Please see the sketch (you can doubleclick the .exe file to view it, it's an e-drawing file) and worksheet in attach.
The Problem is: I have as many equations as unknowns and when i change the guess values, i get always different results.
Are my equations right, and do i define something double or contradictory?
Any help will be appreciated.
Thank you very much for your efforts.
Volker
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I believe you have not formulated it correctly. If you get multiple answers that usually means there are multiple answers. Mathcad stops as soon as it finds one solution. Running a quick check of your results shows that all of the constraints are solved properly with your results. Maybe TOL or CTOL would make a difference, but I doubt it. Check the results to see what isn't making sense.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try please copy the answer and input it as guess value.
Better to have the guess value not as x:=1 y:=2 ets but as two vectors.
As here for example
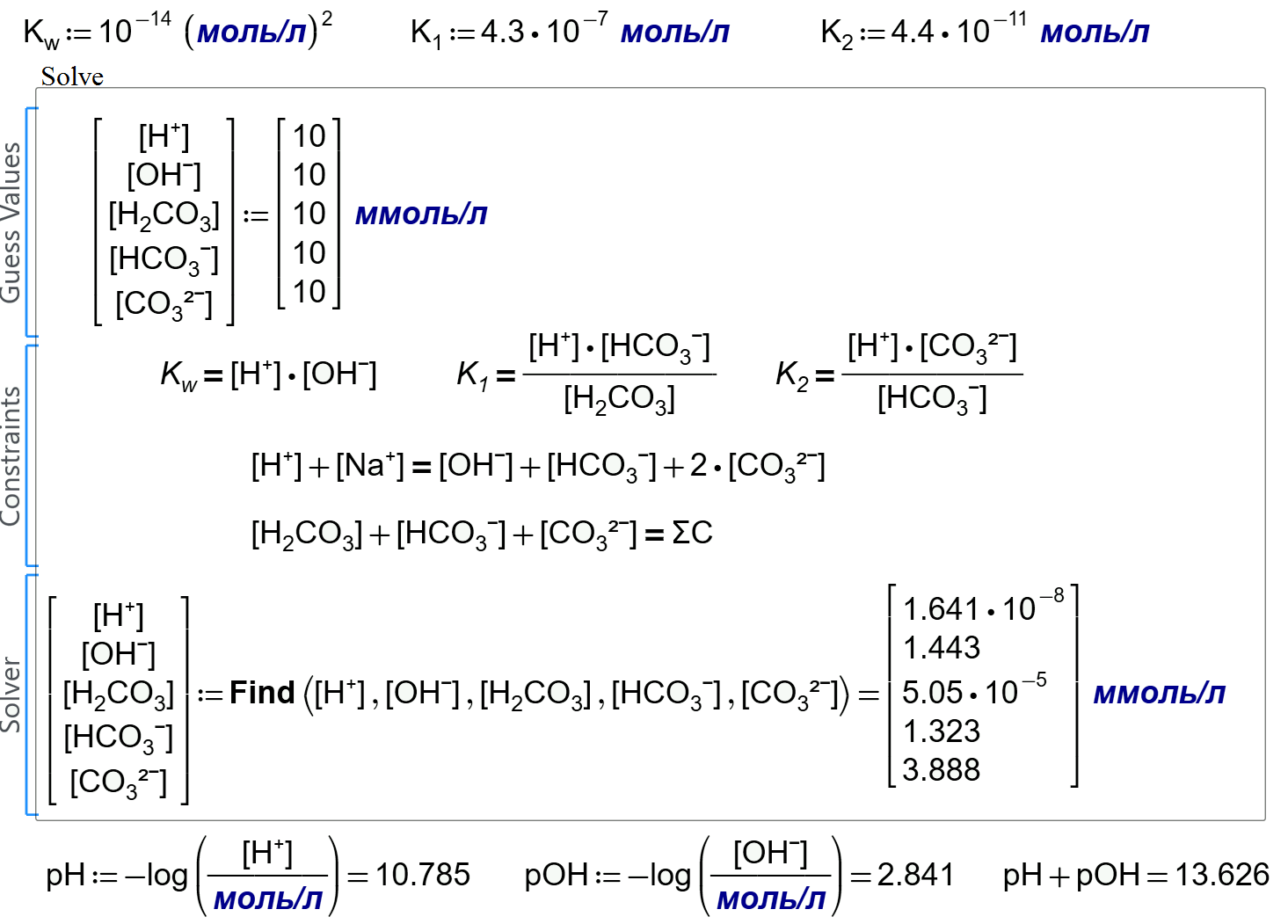
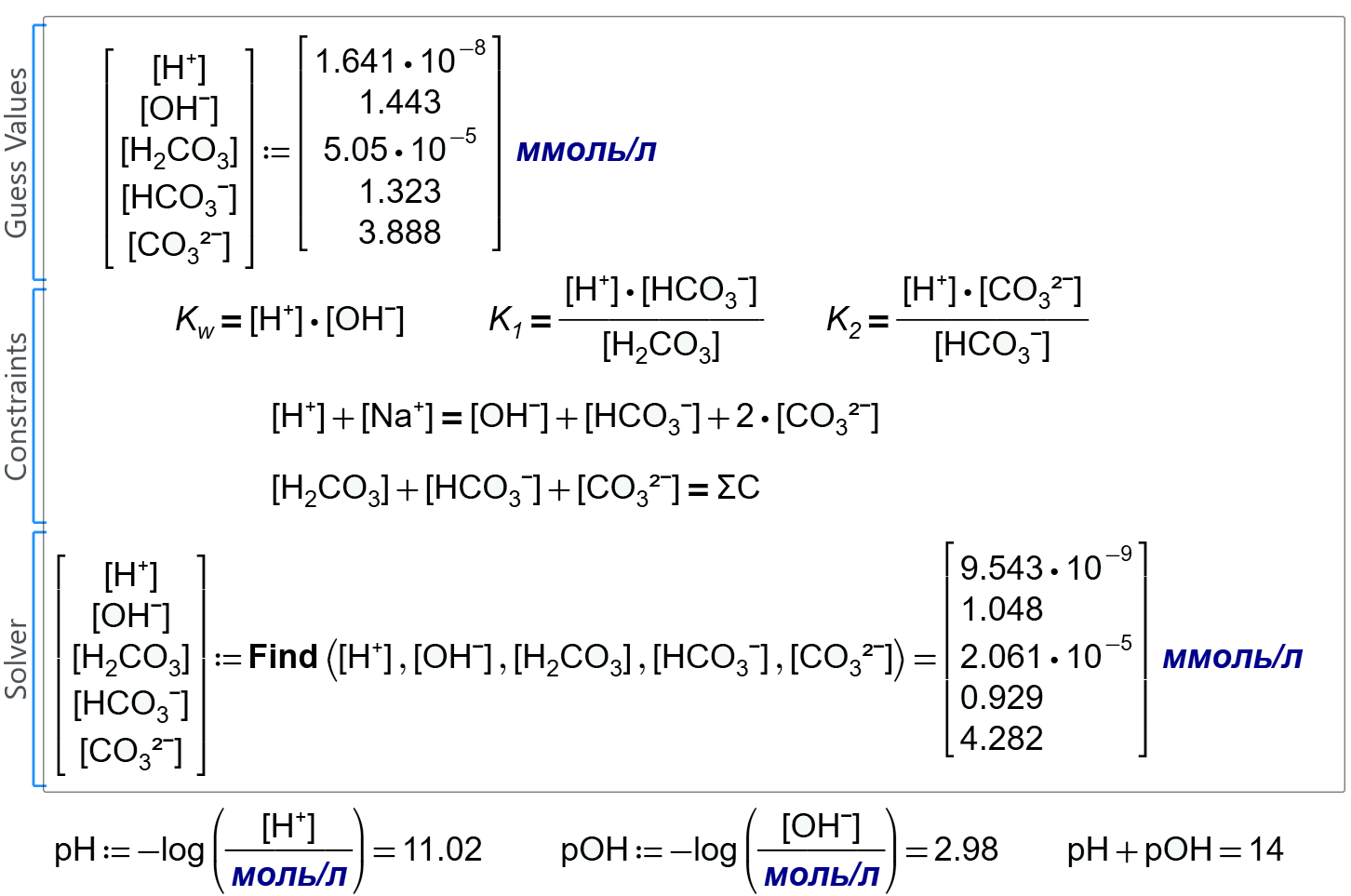
The second answer is correct!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Valery, that's cool idea!
I used the results for guess-values like you did (in Vector-Form) but i got unrealistic results although i checked my equations again after that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know this but i am wondering why there is anyway no appropriate Solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
And second!
Non linrar system can have not one solution!
See please Given-Find Block and Guess value
I like this example of yours and its interesting to see how different algorithms chosen influence the outcome
As we see LM fails if x=0 or y=0.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner!
It is my Van Gogh in Mathcad!
See pleas the english variant of my old article (a chapter from my book):
Решение алгебраических уравнений и систем
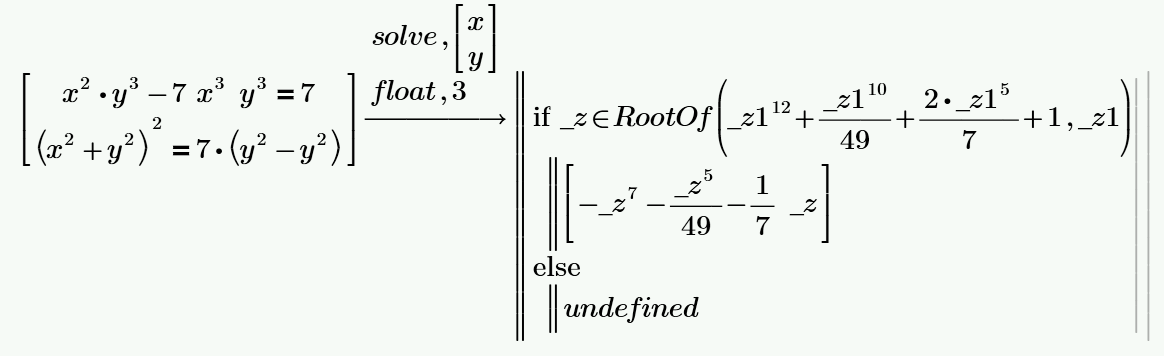
And we have n real roots and plus n^2 or more complex roots!
See one picture from the article (the old good Mathcad 11 + Maple - 4 real roots):

Why "old good"?
See абсолютно точный и абсолютно бесполезный ответ from Mathcad Prime (Mathcad 15) + MuPAD:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Почему у меня не получилось?
Why do I have not same answer?
Sorry
y^2-y^2
but x^2-y^2
![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
As we see LM fails if x=0 or y=0.
Yes!
It is a schwarzes Kreuz from LM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Better to have 7 roots and 7 colors - a rainbow - радуга!
Do you have this example? Слабо?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Valery Ochkov wrote:
And second!
Non linrar system can have not one solution!
See please Given-Find Block and Guess value
I like this example of yours and its interesting to see how different algorithms chosen influence the outcome
As we see LM fails if x=0 or y=0.
Werner!
Send please the Mathcad-sheet!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I believe you have not formulated it correctly. If you get multiple answers that usually means there are multiple answers. Mathcad stops as soon as it finds one solution. Running a quick check of your results shows that all of the constraints are solved properly with your results. Maybe TOL or CTOL would make a difference, but I doubt it. Check the results to see what isn't making sense.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi dferry,
Thank you!
I'll check this again.
You are concentrated to the problem and sorry for the other answes in my thread: I don't need nice animations and Van Goghs-this is out of my topic, i need solutions and that non linear systems can have multiple solutions is clear for me and can be told in one sentence !!!
Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I checked all with boolean:

Of course it is all true because the solver found one solution which fits to all equations!
My Problem here is: Finding the right equation(s) for a practicable solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi dferry,
Thank you again, i have the problem not correctly formulated. There were two Equations lost, which describe the tension completely.
When changing e.g. the guess-values for the forces, the solution keeps stable. When changing the forces to a value which is too far away from the desired solution we get unrealistic results (but the EQN-system is solved as well but at another solution point- that's ok too as far as mathematics is concerned)
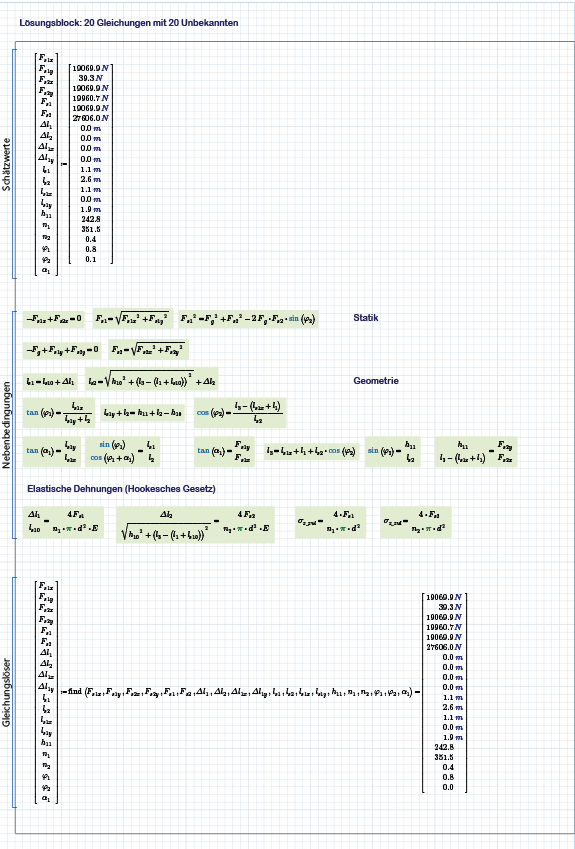

Now it is solved completely.
Best Regards,
Volker