Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve Block, Vary initial Guess Value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve Block, Vary initial Guess Value
Hi guys,
My objective is to find LCC as close as possible to 1.
Upon my Initial Guess Value of 1mm, it returns tcalc3 = 13.803mm
second guess value of tcalc3 = 13.803mm, returns LCC of 0.795 and tcalc3 = 12.3mm
My question is how can I make it as iterative, so that I dont have to keep manually changing the initial guess value (tcalc3) to find LCC close to 1
Thanks!!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The normal way would be to turn the variable assignments into functions of t.calc3, so they can change when t.calc3 changes.

Then use those functions in the equation(s) of the solve block

I am still confused that we get a solution even if we use more than one equation in the solve block but obviously the equations are dependent and redundant and (the right) one of them would suffice. Didn't investigate in this , though.
Anyway - it seems you get what you are looking for
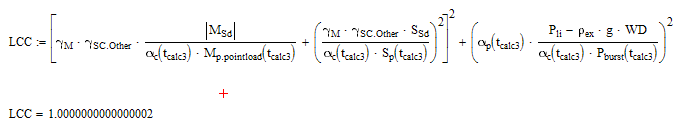
Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may consider posting your worksheet instead of just posting a screenshot, if possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should avoid numeric assignments in solve blocks. They are never necessary, and just make things confusing. In earlier versions of Mathcad it was not even allowed, and, IMO, it should have been left that way. Aside from that, which is just a cosmetic issue, you have four equations in your solve block and are only solving for one unknown. That's a problem, and the solve block is not doing what you think it is (I'm somewhat surprised it doesn't just give you an error). If the solve block is structured correctly it will give you the value of tcalc3 that makes LCC equal to 1, if such a value exists, or as close to 1 as possible if it doesn't. Please post your worksheet (in the edit dialog, click on "Use advanced editor" at the top right").
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Please find the attached documents,Thanks for your help. How do I assigned the programming without using the numeric assignments?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The normal way would be to turn the variable assignments into functions of t.calc3, so they can change when t.calc3 changes.

Then use those functions in the equation(s) of the solve block

I am still confused that we get a solution even if we use more than one equation in the solve block but obviously the equations are dependent and redundant and (the right) one of them would suffice. Didn't investigate in this , though.
Anyway - it seems you get what you are looking for
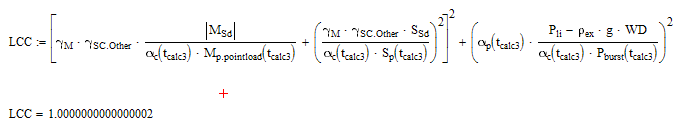
Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am still confused that we get a solution even if we use more than one equation in the solve block but obviously the equations are dependent and redundant and (the right) one of them would suffice. Didn't investigate in this , though.
Just get rid of the first three equations. There are equivalent numeric definitions of these in the body of the worksheet. As definitions, the first is used in the third equation. The second and third are used in the fourth equation. That's why it works with four equations: they are just a sequence of dependent functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, yes. Just like I suspected. I had not taken the time to study this in more details, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner
Thanks alot! it works by changing the alphaTC, beta etc as a function of tcalc3





