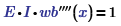Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve System of Differential Equations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve System of Differential Equations
Hi I am trying to solve system of 2 ODE as shown below. I am unable to find out the issue.
The error happens when I m trying to relate the first ode to the second one. I am getting error as "Unknown error: ode% _function% _illegal % _context. Please help!
- Labels:
-
Civil_Engineering
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please attach your Prime worksheet.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
The calculation has been done at the bottom of the mathcad sheet. Please see attached.
Thanks
Sukrit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have a look here https://community.ptc.com/t5/Mathcad/Multiple-ODE-s-in-MathCad/m-p/785905#M200434
Similar problem, solved.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So its not possible in Mathcad Prime in a solve block?
Symbolic Math is not incorporated well in the Mathcad software like Mathematica.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It IS possible using a solve block, but it takes a little effort. Have a close look on what @Werner_E accomplished in that thread.
Alternatively you should be able to solve it symbolically in Prime. For that you'd have to make use of my latest addition to https://community.ptc.com/t5/Mathcad/Toolbox-Solving-Ordinary-Differential-Equations-symbolically/m-p/689336#M192090 .
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Feature does not work on Mathcad Prime. 😞 MATHCAD so full of bugs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
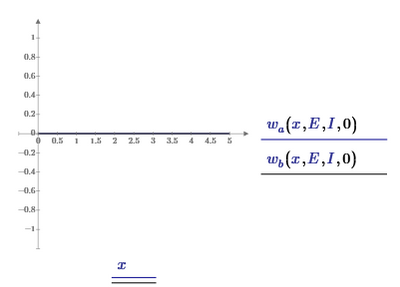
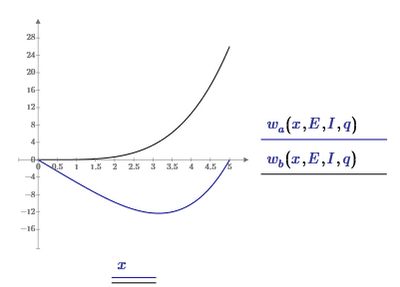
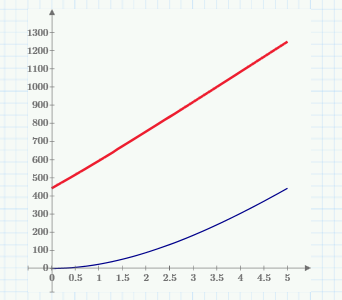
With your set of ODE's this is the result:
but if your ode's are
and
you may get:
See attachment for further details.
(For further information on the solving of ODE's refer to https://community.ptc.com/t5/Mathcad/Toolbox-Solving-Ordinary-Differential-Equations-symbolically/m-p/689336#M192090 and have a look at the Prime file in there.)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm!
Express, using integration and boundary conditions to solve for constants of integration:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
I guess yours is the correct result.
After checking a few items in my sheet, I find that the solution of w00 through w07 is incorrect.
If I have time later, I'll check my method with Mathcad 11.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Found the culprit. Prime has this nice '-operator (quote, gives the derivative), but it is apparently only intended for single parameter functions, such as f(x), but not for f(x,y,z).
So I ended up defining the derivatives explicitly and then solving for the initial conditions. That results in the correct answers.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Luc, it looks like a solution without using solve block feature.
I might write 8 equations by integrating each of the Differential equation 4 times and then substitute the boundary condition and solve the problem by finding unknowns. The program does not automatically catch boundary conditions establishing a relationship of one differential equation to another.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't use solve blocks (I only have Express), but by integrating and applying boundary conditions to evaluate integration constants we can still address this problem. I doubt that you intended to set such a simple problem. Attached is Prime 4 discussion.