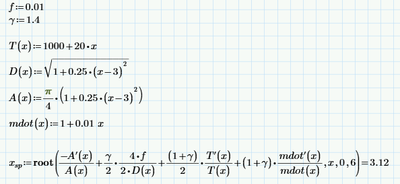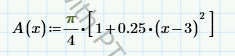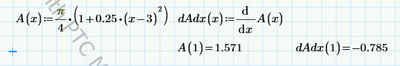ACCEPTED SOLUTION
Accepted Solutions
As Fred indicated, your problem is caused by using square brackets in the wrong place.
If you type an expression and want to keep a part of it together, you should ONLY use round brackets: ( and ).
Note that if you type the opening bracket ( Prime will create the pair ( and ).
You should never type square brackets in an expression in order to 'bracket' a part of that expression. Prime will change round brackets to square brackets automatically if there's a need for it (or whenever it feels like); but you should never type them for that purpose.
There are two uses for square brackets:
-You type a [ in blank space or adjacent to an operator to create an array (a vector or a Matrix), here too Prime will create the pair [ and ].
-You type a [ immediately adjacent to a variable to add an index to that variable. In that case the variable must be/hold an array.
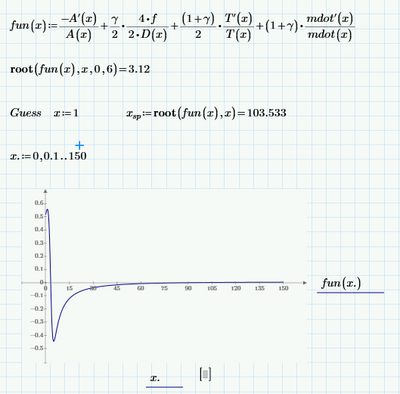
That said, your worksheet doesn't need to define the derivatives explicitly, and it doesn't need the solve block. It could look like this:
The prime operator ' takes the derivative of the function it is attached to. The function must be a single parameter function. All your functions are single parameter, they only have x, so it can be used here.
The root function takes two or four parameters, the first two of which are a function and a variable (that must be a parameter of the function). It searches for a value of that variable where the function value is zero. The third and fourth parameters to root define the boundaries for the variable between which the zero should be found. Alternatively you can define a guess value for the parameter before calling root, different guess values may produce different roots, depending on the function. Note that root does NOT always find the root closest to the guess value.
In case of surprise, check the function by plotting it.
Success!
Luc
When you used the square brackets,
you created a one- valued vector, so the derivative function doesn't work
Try eliminating the square brackets:
As Fred indicated, your problem is caused by using square brackets in the wrong place.
If you type an expression and want to keep a part of it together, you should ONLY use round brackets: ( and ).
Note that if you type the opening bracket ( Prime will create the pair ( and ).
You should never type square brackets in an expression in order to 'bracket' a part of that expression. Prime will change round brackets to square brackets automatically if there's a need for it (or whenever it feels like); but you should never type them for that purpose.
There are two uses for square brackets:
-You type a [ in blank space or adjacent to an operator to create an array (a vector or a Matrix), here too Prime will create the pair [ and ].
-You type a [ immediately adjacent to a variable to add an index to that variable. In that case the variable must be/hold an array.
That said, your worksheet doesn't need to define the derivatives explicitly, and it doesn't need the solve block. It could look like this:
The prime operator ' takes the derivative of the function it is attached to. The function must be a single parameter function. All your functions are single parameter, they only have x, so it can be used here.
The root function takes two or four parameters, the first two of which are a function and a variable (that must be a parameter of the function). It searches for a value of that variable where the function value is zero. The third and fourth parameters to root define the boundaries for the variable between which the zero should be found. Alternatively you can define a guess value for the parameter before calling root, different guess values may produce different roots, depending on the function. Note that root does NOT always find the root closest to the guess value.
In case of surprise, check the function by plotting it.
Success!
Luc
