Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve block problem (3.1)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve block problem (3.1)
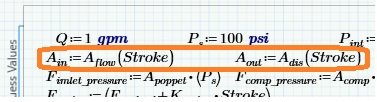
I have what I thought was a fairly simple problem, but it is giving me all sorts of problems converging. Background: I'm solving for flow and forces on a valve to find conditions as the valve strokes. So, I have flow through a series of orifices (solving for an intermediate pressure) and those pressures lead to forces that must balance against other forces (e.g. a spring). So, it solves that without any issue. Then I want to get more complicated and I use the solve block to calculate a simple parameter like flow velocity - then it starts having trouble. Note, velocity doesn't affect the flow or force equations - I'm just looking for a value. Sometimes it will solve it, but I have to get the guesses right on. So, am I not formulating this right? The blocks in red are what cause a problem when I enable them. I've tried many ways of entering the guess values but nothing seems very robust. Thanks!

3.1 and pdf attached.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It looks to me that the red areas should not be insider the solve block as the values can be calculated after the solve block.
You may create a function ans2 which first call ans an then calculates the two values.
But I guess on the other hand that those read areas should not do any harm either.
Do you mean that you get a continuous curve in the last plot if you delete the red areas and the last two entries in the find statement?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner. Unfortunately there is a bit more to the problem than what I show here that would prevent ans2 from working. Eventually, V_inlet and it's partner DP_in would get fed back into lower the value of Ps (so DP_in is an inlet loss). However, since I (or mathcad) struggle at this simple stage I don't have any better results with that approach even if its a true iterative problem at that point. So I was tracing everything backwards to find when things go awry. While it's possible they aren't necessarily the same problem, I thought this was worthy of posting since it seems to be misbehaving. As to your second point - yes - if I delete the areas in red I get a continuous curve (it would then be identical to the first solve block).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately I can't read P3.1 files, so I can't play around with it.
But on first sight it looks like a bug.
Would be interesting to see if it is possible to vastly simplify the solve block and nonetheless reproduce that erroneous behavior.
Some ideas:
- Have you tried to play with the settings of TOL and CTOL?
- If you rewrite the whole thing just for research to work without units - is the effect still there?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
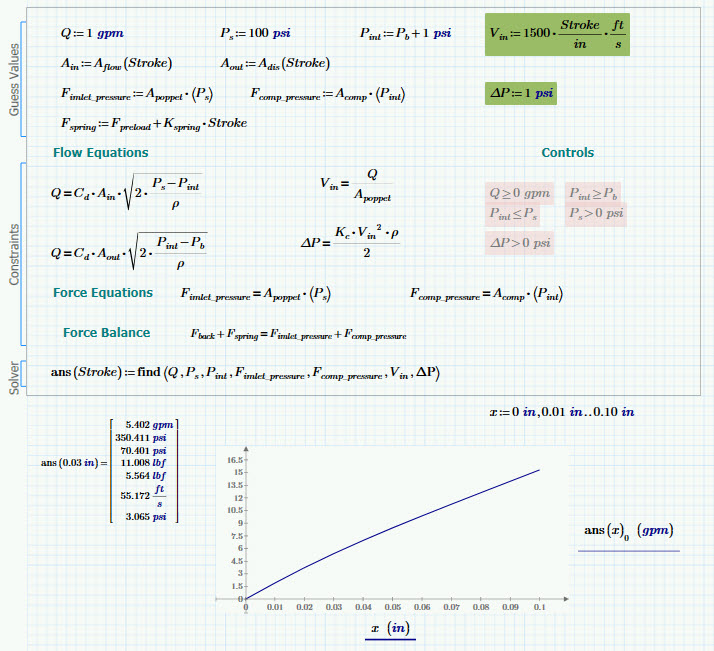
Those are good suggestions. TOL/CTOL had no effect. I may try it without units but not today. However, in the meantime I have something that appears to be quite robust. Here's what it takes:
- A good guess for V_in
- A simple guess for DP (this seems to be the main key. If I give in the equation it struggles.)
- Removal on the > < constraints (which I thought would help, but apparently not) Q and DP seem to be the worst offenders but it doesn't need any of them.
So, based on that I'm suspecting it was somehow finding itself over constrained and only sometimes able to find a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Removal on the > < constraints (which I thought would help, but apparently not) Q and DP seem to be the worst offenders but it doesn't need any of them.
It looks to me that those <, > constraints aren't necessary and are maybe counterproductive because your system of 7 equations in 7 variables has unique solutions - no room for additional constraints.
You may even solve your system symbolically and use those expressions to calculate your variables if you want to be an the safe side and avoid the undesired effects of the numeric solve block:

Of course you would have to replace A.in, A.out and F.spring with functions dependent on "Stroke".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
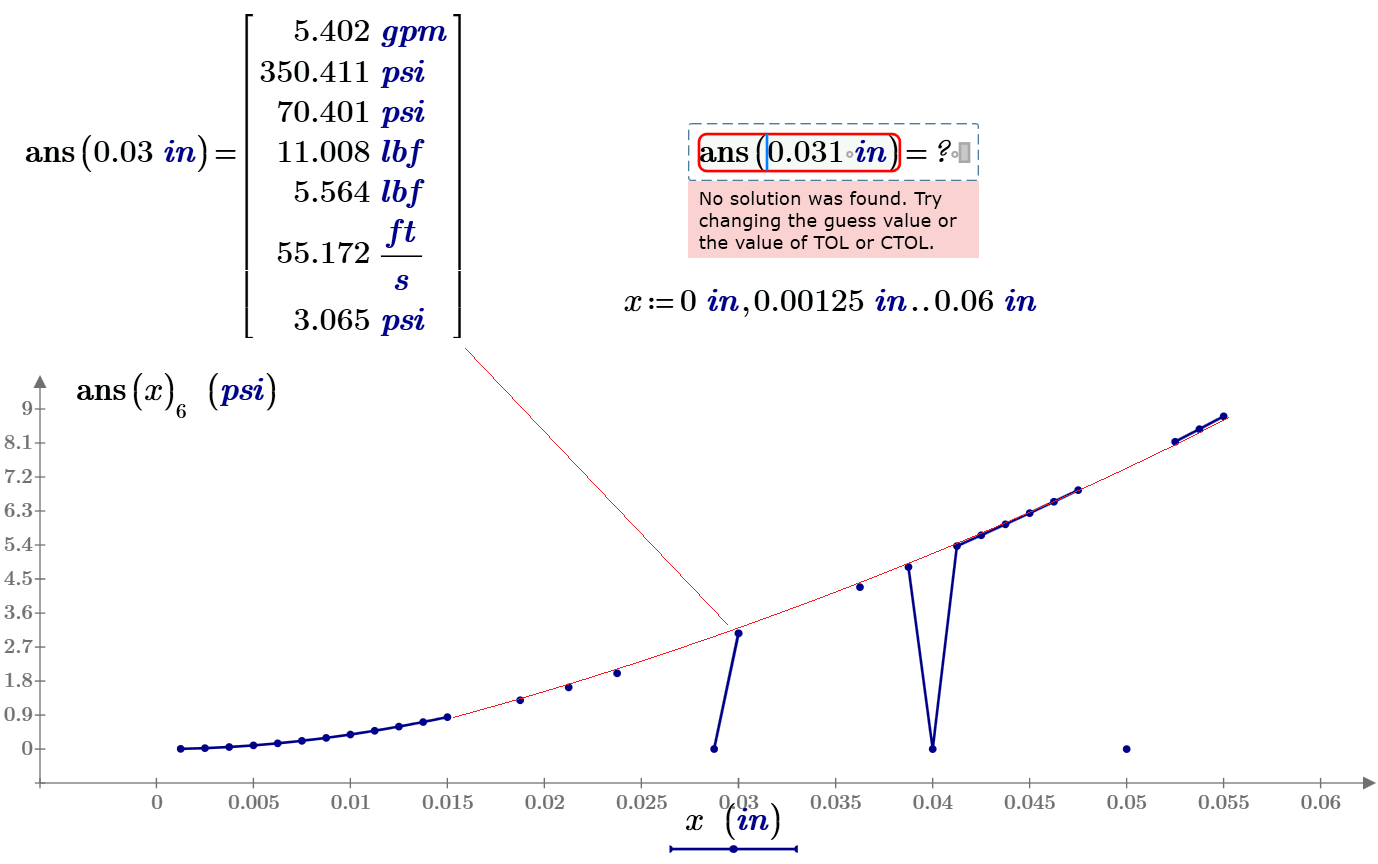
You have solution but not for all points of the range variable x. And some points has wrong solution.
See in the book Thermal Engineering studies with Excel, Mathcad and Internet the Fig 17.14 here Study 17. Cogeneration (CHP), trigeneration (CCHP) and quadrogeneration (CCHPI) or how much of mathematic is contained in thermal engineering
I have had same problem for one Chemical task and must use not the Given-Find block but own program with the method of successive approximations and root function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
I do apologize but I'm not sure I understand where you are trying to lead me. Successive approximation isn't something I've played with before. (Just a hunch, but did you attach the correct file? It doesn't seem to contain your posted solution so I'm not sure how to go down your proposed path. But I'm eager to learn and so far google hasn't shown me what I need to be doing.)
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure how you used root (and I'm not sure it would work in the full 12 page version of my sheet this is based on), but I think I was able to figure out how to use successive approximation with the solve block. I wasn't aware that I could feed new guesses into a solve block, but it seems to work. But that's why I ask the experts here. Mathcad is still buggy solving this, but with the right guess for P_int and specifying Q>0 it solves reliably and virtually instantaneously. Before it could take 5-10 seconds to solve 10 points.
3.1 file attached. The important steps are in purple below.
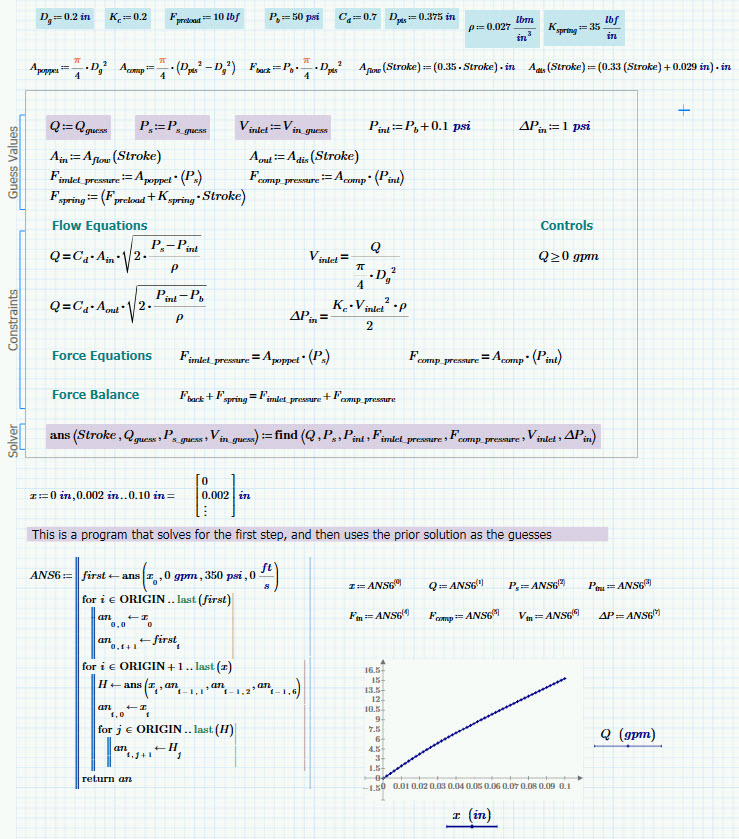
Since I couldn't find any examples of this, I think I'll post it as it's own topic under a more searchable title.
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi dferry,
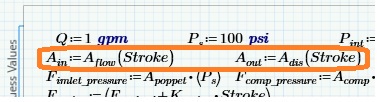
If the initial guess of "Stroke" is undefined, so are Ain and Aout. I am amazed that there are results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. написал(а):
Hi dferry,
If the initial guess of "Stroke" is undefined, so are Ain and Aout. I am amazed that there are results.
Sorry - all is correct - the find function returns not a value but a function with the argument Stoke.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks! there is always time to learn new things...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That was one of my discoveries through this adventure. I formulated it many, many ways. I think the takeaway is that when something is defined as I've done here, but those values aren't called out in the FIND function, mathcad solves it once and uses it as a fixed value. Which is exactly what is needed. Made it much, much faster than leaving A_in as a function of stroke. (In the full-up model calculating A_in is much more elaborate that what I do here). It seems to work anyway, although it's possible it is causing my problems.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And what can You say about my reply?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
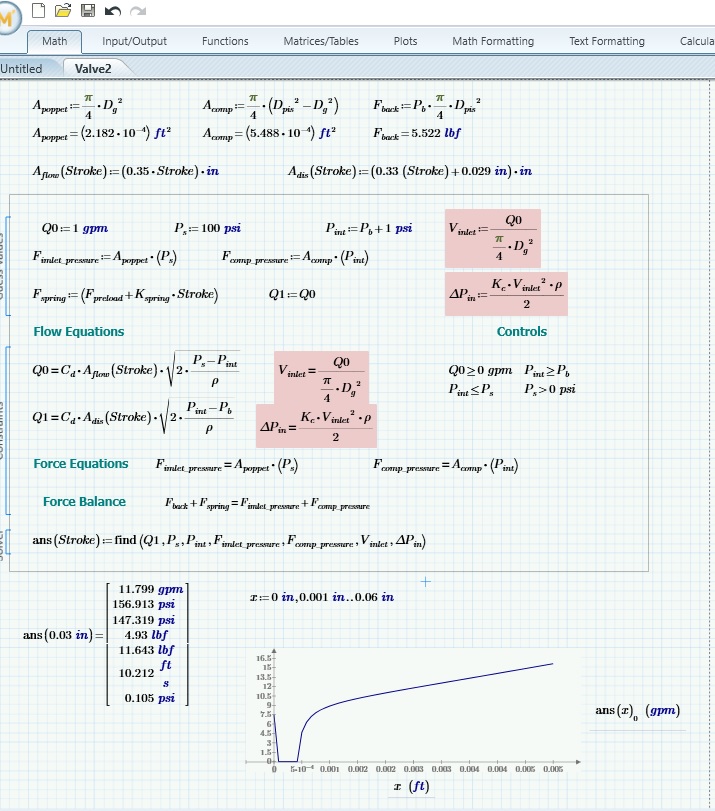
What surprises me is that in the solve block, Q is defined in two different ways. So I made a change ....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
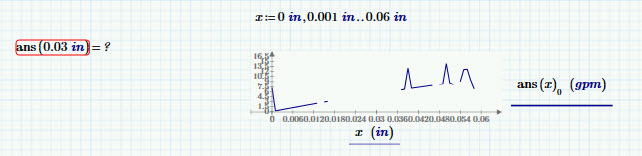
The problem there is that Q0 isn't resolved and remains as the guessed value (1 gpm). Switching Q1 = Q2 to a constrain (instead of a guess) and adding it to the FIND doesn't work out too well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

To give you a complete help I should know the analytical study of the problem. Directly addressing the problem on the worksheet, we go groping. The best way to solve a problem that creates others, is to start all over again being a little more careful.
Bye
F.M.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Read please my letters