Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve by using MATHCAD_Prime3
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve by using MATHCAD_Prime3
Dear all,
I need your help to solve this minimization (by symbolic calculation) using MathCAD Prime 3 that I have and use at school.
In ordrer to be clear, I attached a picture of what I want to solve. Note that both x, SNR and BER are real positive values.
I will be happy with your help.
Bests,
Max Fréjus
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think - only numerical!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Max.
Sorry, but this isn't a joke: As it is stated the problem, if f approx= 0, the minimum is zero. The minimum of a function is the value of this function, not where the value appear. In other words, you can't solve for the minimum of f(x)=0, but for the minimum of f(x). Maybe your problem have another question, like where the minimum occur that's for which x, or for which ranges of SNR and BER constants.
Also, some background could be help, like the origin of the problem and constants.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you M. AlvaroDiaz for you return. Ofcourse, May be I need to reformulate the problem. I understand what you mean. In fact, f(x) is obtained from the difference between two components that are supposed to be equal to each other. THE CONSTRAINTS I have are like these: x is the variable which is strictly positive; SNR and BER are constantes positive values that I can change to emulate my model (they are all known).
Like I Said that I have two components in terms of variable x that are equal together, to solve this by symbolic calculation with Mathcad Prime 3 (I can do it numerically with matlab), I propose to minimize ther difference which I called f(x) to check the expression of x that will give me or approximate f(x)=0.
That is what I need to do, if I was Clear by my explanation. Hope that information Will Help you to understand the problem.
thank you and best !
Max
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Max. There are no hope to have a symb expression for that. First, you need some one for inverse erfc, and I don't know any one. As Valery says, only numericals.
In general, if you have looking for x that makes m(x) = n(x) what you need to minimize is abs( m(x) - n(x) ) or something else like squares, avoiding negative values. If not, the minimun could be - infinity.
In the picture, the numeric implementation for the inverse of erfc in mathcad. If you want a symbolic expression for its derivative, please check this link: Wolfram|Alpha: Computational Knowledge Engine . Notice that substituting the minus by an equal don't give any answer.
Best regards.
Alvaro.
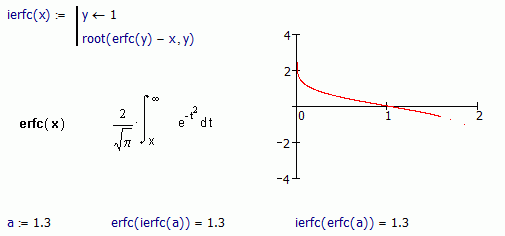
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Max. F.
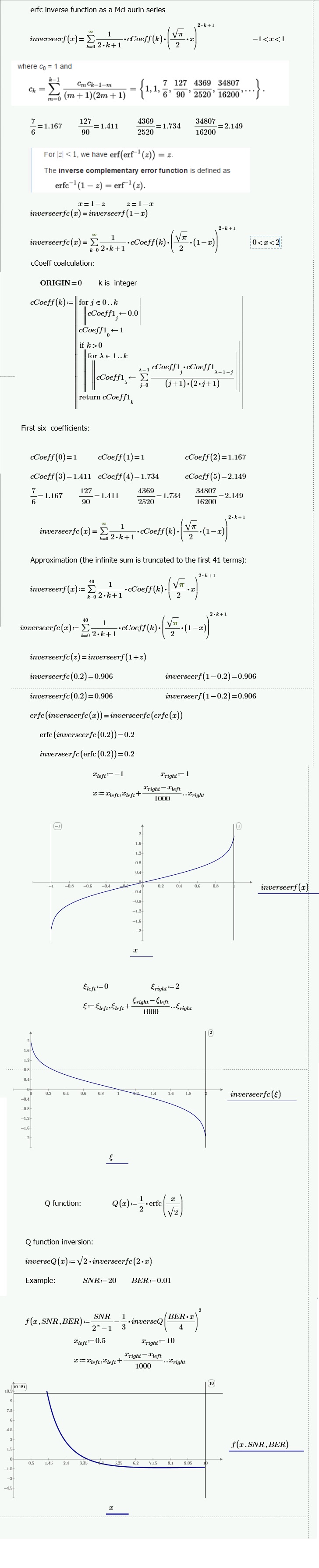
The picture represents only the first part of the solution of the problem which is to be checked.
Indeed, let me know if I'm on the right track. Moreover, you may also continue for yourself.
Greetings.
FM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi F.M. By root finding, I get ierfc(0.2) = 0.90702.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for all your help dear M. AlvaroDiaz and F.M. !
All your help is real greatful. Sure, like M. AlvaroDiaz said, I have a mistake in my formulation. As I have something like this : m(x) = n(x), I need to minimize in easy way, f( x ) = abs( m(x) - n(x) ) or something else like the square method. In my case, it is --> f( x ) = abs( m(x) - n(x) ) where : x is the strictly positive variable, m ( x ) = A/(2^x-1) ; n ( x ) =1/3*2*InverseErfc(B*x/2)^2 ; and A, B real positive values.
Sure, it is clear to ckeck first the numeric implementation for the inverse of erfc in mathcad and later solve the minimization if it's possible. For that, I thank you all for your rapid return with picture illustration.
But, I'm a kind of new user beginner in Mathcad Prime, is it possible for you to share with me your mathcad project when trying to help me by sending the picture. I mean, instead of the picture, is it possible to send me mathcad file?
Thanks again ! And Bests,
Max Fréjus
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unser Freund Max, braucht eine analytische Lösung, nicht eine numerische Lösung.
Bezüglich meines Berechnungen, es ist alles OK bisher.
Danke für den Hinweise über meine incorrect numerische berechnung.
Viele Grüße
FM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mein Lieber Max, "Du möchtest die Kokosnuss, gereignet und gut.".... Übst Du, ein wenig, zu Kopieren und zu digitieren mit der Tastatur.
Tschüss
FM






