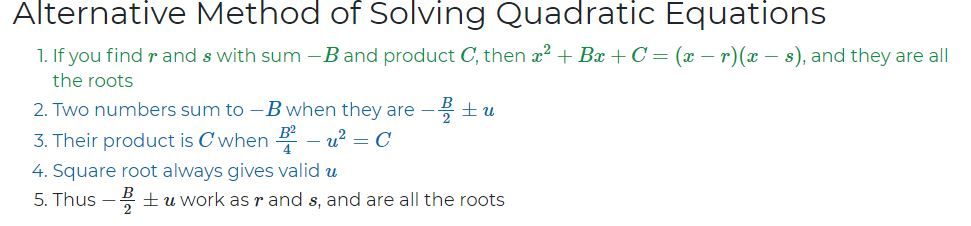Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving a quadratic equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving a quadratic equation
New and old from Po Shen Loh
- Labels:
-
Math Homework
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
6. Where u=sqrt(B^2/4-C).
Simply:
This is the famous quadratic root formula, but with A=1.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the famous quadratic root formula, but with A=1.
Well, duh! You didn't expect a different answer, did you? 😉
What I found noteworthy, that maybe didn't come across in my post, was the development of the solution in his paper, https://arxiv.org/abs/1910.06709, was the logic behind the derivation. (I like starting from basics and developing the solution rather than memorizing an equation. Probably because my memory is so poor.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First off: I did not mean to be offensive in any way. Please accept my apologies if my reaction came across that way.
No, I did not expect a different answer.
Unfortunately the link you provide does not work (for me), but I was able to follow the gist of the 'derivation' by the 5 steps. I felt that the calculation to find the value of u should be explicit, rather than just hinted at in step 4. Hence my step 6; in hindsight this should be added to step 4.
Note that the method also works for Ax^2+Bx+C=0 as follows: Divide the entire quadratic by A, gives you x^2 + B'x+C'=0, with B'=B/A and C'=C/A.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I took no offense, and hope I didn't give any.
Try a Google search on "po shen loh quadratic equation" which should point you to https://www.nytimes.com/2020/02/05/science/quadratic-equations-algebra.html eventually.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That link works immediately. Thanks!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
.....
Unfortunately the link you provide does not work (for me),
The comma after the address was mistakenly still part of the link. So it should only be
https://arxiv.org/abs/1910.06709
A nice find.