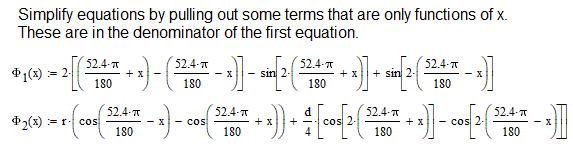Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving equations system
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving equations system
According to some web tutorials, I have tried to solve the equations system you can find in the attached figure.
I want to solve the system in order to find variables x and e. All the other variables are defined (you can see defined values also for e and x, they are guess values according to tutorials).
I am not able to find out what is my mistake, if I click on "sol" I see the error "This variable is undefined".
You find also the Mathcad file attached.
Can someone help me?
Sincerely
Stefano Grandi
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Two issues here. One solvable, one not.
Firstly, to use the Find(x) function to solve a system, you must place a Given command before your two equation constraints.
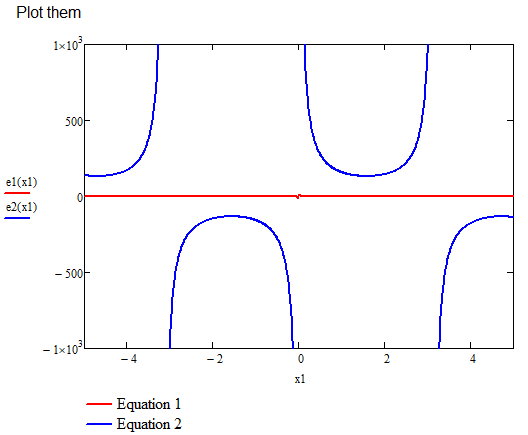
Secondly, before solving anything, always plot your data. If we rearrange the first equation, putting variable e on the left side (it is separable) and call this e1(x), we can get an idea of how this equation behaves. Rearranging the second equation in terms of e and calling this e2(x) gives a look at how both equations look and where they may intersect.
They do not intersect. There is no solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The "Given" keyword needs to be placed after the guess values and before the equations of the solve block.
With the two equations as they stand Fm.c=5 and T=2000 you can set x, e to get 5 and 2000 but not with the same values.
Please check your equations.
Solve block works Fm.c=5 and T=2 to show you it can work if equations are solvable.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much @terryhendicott and @JeffH1!
I solved my issue and I will keep in mind to plot curves before.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Two issues here. One solvable, one not.
Firstly, to use the Find(x) function to solve a system, you must place a Given command before your two equation constraints.
Secondly, before solving anything, always plot your data. If we rearrange the first equation, putting variable e on the left side (it is separable) and call this e1(x), we can get an idea of how this equation behaves. Rearranging the second equation in terms of e and calling this e2(x) gives a look at how both equations look and where they may intersect.
They do not intersect. There is no solution.