Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving equations using using arrays
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving equations using using arrays
The attached contains an expression I wish to use in a solver to determine x-amount of constants (the Q's) from a system of an equal amount of equations and unknowns (the constants). The problem in mathcad arises when I'm using multiple (two) arrays within the solve block.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As already suggested, get rid of the summation and the indexing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You will have to specify a value for n first.
You will also have to provide at least a sample for the vector u and the square matrix lamda.Q so we have soemthing to play with.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can it be that you are looking for something like the attached?
EDIT: Of course you can get the result much easier using the inverse:
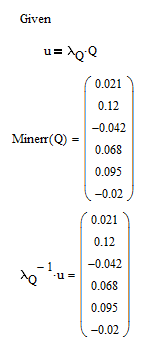
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Something like that but I need to include summation over one of the indices.
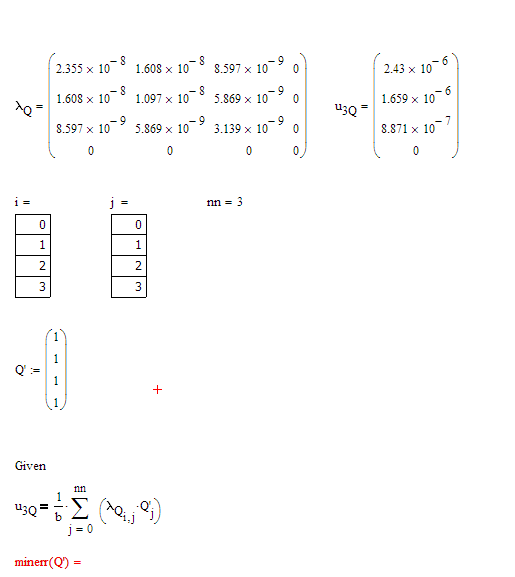
"Funny" thing is I got it working a few minutes ago but the Mathcad shut down spontaneously and I can't get it working again. The error message is:"This variable is undefined"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What you set up with your sum is exactly the multiplication of the matrix lamda.Q with the vector Q - thats the reason I posted my sheet in the last message. ![]()
The error messages in solve blocks are misleading - you will always get that "undefined variable", no matter what the real cause is. Right klick at the error message and chose "Trace Error" to get at least a message which may be a bit more useful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've entered exactly what you you did in the attached but I still get that same error. It can be traced to the "i" index that supposedly has to be an integer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please post your worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please post the actual worksheet an image is no good in this instance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As already suggested, get rid of the summation and the indexing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're absolutely right and it works perfectly now. I initially dismissed it as being too simple to be correct but I guess I need to brush up on my matrix multiplication rules. Thank you so much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Everything up until the graph goes in to creating the lambda_Q and u_3Q matricess for a known Q matrix. The solve block is an attempt at solving the inversed problem where lambda and u are known and Q is sought.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have managed to return results but I am not sure if it is what you are after.





