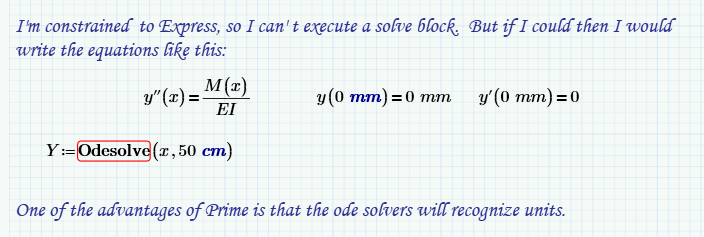- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving for series of equations that include functions, derivatives, and boundary conditions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving for series of equations that include functions, derivatives, and boundary conditions
Hi,
I am trying to solve a beam bending problem. My end goal is to solve a problem with more complexity, but for now I have simplified it so that I can make sure I understand how to use MathCAD.
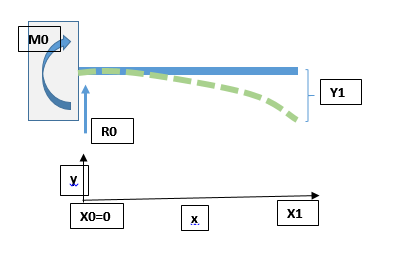
See the sketch below. I have a cantilever beam, supported on the left (at x0=0) it extends to x1. The Support reaction loads can be described as M0 and R0 which I am trying to solve for. The end of the beam is being deflected by Y1.
I have set up a solve block in MathCAD (Prime 2.0) as such:
But I get all sorts of errors. I've been reading about different solving methods including odesolve (I guess this could be seen as a really simple ODE, as well as symbolic calculation, but I haven't gotten any to work! Can anyone help me solve this? See the Sheet attached for the example.
Cheers,
Raz
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This, in the way it is shown, will definitely NOT work with any version of Prime to date, nor with any version of Mathcad other than 11.
If you need to do a lot of this kind of stuff, symbolically, you can use the symbolics of Mathcad or Prime to help you solve Differential Equations via the Laplace domain (essentially that's what my sheet in Mathcad 11 does). But it involves work by you. If you want ready symbolic solutions to DE's out of the box, then you need to resort to other applications: Maple & Mathematica are two of the most powerful I know of, you may want to check out Maxima (it's free). (Why do all names of these applications start with "Ma"?)
It so happens that the symbolic machine in Mathcad 11 is Maple. As of Mathcad 14 they replaced that with MuPad. (Ah, that one's not part of the pack!)
But... If you can live with numeric solutions, Mathcad will be your friend, and if you then need to include units as well, then Prime may be your better friend.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
But I think the Odesolve function is not for a boundary problem! We must use shooting method!
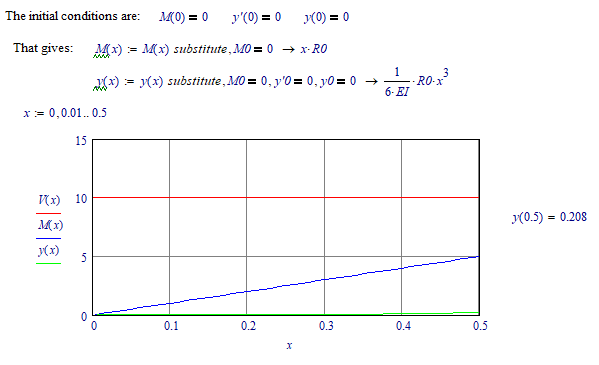
This is not really a boundary value problem. If you write the second order ODE for y, you have two initial conditions y(0)=0, and y'(0)=0. (A cantilever, fixed, end.)
He needs to think/learn about how to formulate the problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred, Thank you for your help - I recreated the solution in my sheet, however I am running into some roadblocks. By the way, I really appreciate that your method includes units.
With the Euler method, I have defined the input forces (R0:=10N) and then solved for the displacement, but I am trying to do the opposite. I am trying to input the displacement at the end of the beam and then solve for the reaction force.
In other words, the boundary condition y(x1)=Y1 was not maintained.
In this case, I can decrease my initial guess for R0 to 10N*(10mm/41.66mm) and I will get the a satisfactory solution, however this recursive method may fall apart once I try to expand this solution to a more complicated beam with multiple supports.
Do you have any suggestions for how to rewire the solution to solve for the resultant force?
Thanks again for the help - by the way, how do you mean "think/learn about how to formulate the problem"? I can solve this problem by hand, symbolically, is there a way to formulate the problem in mathCAD so it can do the same?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@RazBaz wrote:
Fred, Thank you for your help - I recreated the solution in my sheet, however I am running into some roadblocks. By the way, I really appreciate that your method includes units.
With the Euler method, I have defined the input forces (R0:=10N) and then solved for the displacement, but I am trying to do the opposite. I am trying to input the displacement at the end of the beam and then solve for the reaction force.
In other words, the boundary condition y(x1)=Y1 was not maintained.
In this case, I can decrease my initial guess for R0 to 10N*(10mm/41.66mm) and I will get the a satisfactory solution, however this recursive method may fall apart once I try to expand this solution to a more complicated beam with multiple supports.
Do you have any suggestions for how to rewire the solution to solve for the resultant force?
Thanks again for the help - by the way, how do you mean "think/learn about how to formulate the problem"? I can solve this problem by hand, symbolically, is there a way to formulate the problem in mathCAD so it can do the same?
This problem is a spring--it follows Hooke's law. So the end deflection is a constant times the load. You know the deflection for 10 N is 41.66mm, A simple ratio will give you the load for any desired deflection. For 10 mm, R0 = 10mm/41.666 mm X 10 N = 2.400 N
I would set the solve block up for Odesolve like this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
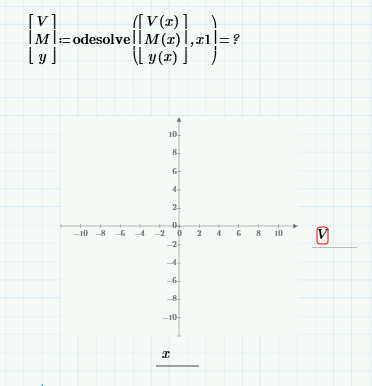
Thanks for trying to solve it this way Fred! I input that data into my solve block and I get an error highlighting the 'x' in the Odesolve function that says that "The arguments of the Odesolve are not correctly specified"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"I can solve this problem by hand, symbolically, is there a way to formulate the problem in mathCAD so it can do the same?"
Mathcad has no provision to symbolically solve differential equations (DE). With simple DE some simple manipulation is possible that gives satisfactory results.
Starting with your initial formulation of the problem this is how you could go about:
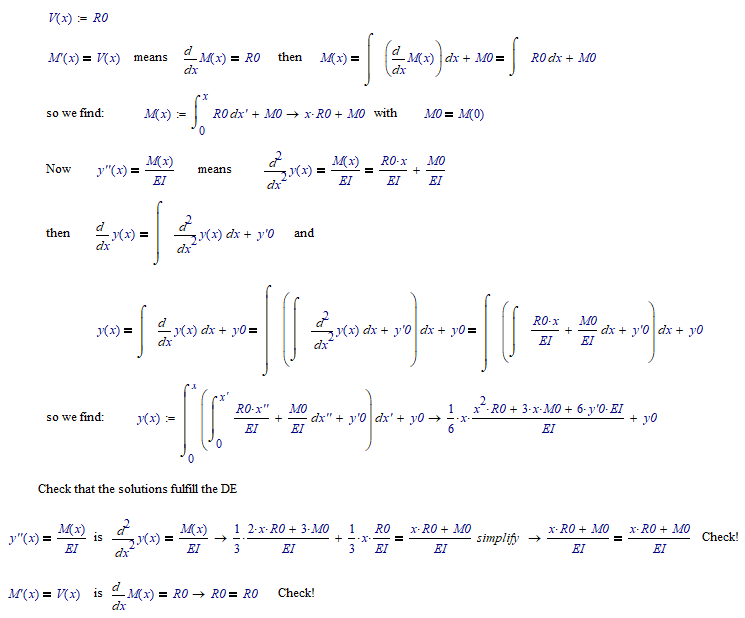
Mathcad 11 file attached.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc, If I understand correctly, this example uses MathCAD to help do the arithmetic steps in the hand calculations. This may be useful since my more complex example gets into the weeds with so many different variables flying around
@LucMeekes wrote:
"I can solve this problem by hand, symbolically, is there a way to formulate the problem in mathCAD so it can do the same?"
Mathcad has no provision to symbolically solve differential equations (DE). With simple DE some simple manipulation is possible that gives satisfactory results.
Starting with your initial formulation of the problem this is how you could go about:
With that settled, we can go on:
Mathcad 11 file attached.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well OK, with Mathcad 11 (but just that version, nothing before, and nothing after) you can automate this completely for solving y(x):
For more information look here:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Whoa that looked like magic to me - but you're saying this definitely won't work with mathcad prime?
@LucMeekes wrote:
Well OK, with Mathcad 11 (but just that version, nothing before, and nothing after) you can automate this completely for solving y(x):
For more information look here:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This, in the way it is shown, will definitely NOT work with any version of Prime to date, nor with any version of Mathcad other than 11.
If you need to do a lot of this kind of stuff, symbolically, you can use the symbolics of Mathcad or Prime to help you solve Differential Equations via the Laplace domain (essentially that's what my sheet in Mathcad 11 does). But it involves work by you. If you want ready symbolic solutions to DE's out of the box, then you need to resort to other applications: Maple & Mathematica are two of the most powerful I know of, you may want to check out Maxima (it's free). (Why do all names of these applications start with "Ma"?)
It so happens that the symbolic machine in Mathcad 11 is Maple. As of Mathcad 14 they replaced that with MuPad. (Ah, that one's not part of the pack!)
But... If you can live with numeric solutions, Mathcad will be your friend, and if you then need to include units as well, then Prime may be your better friend.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery thanks for the response,
Your solution didn't work for me, or I am doing something incorrect with the setup. Here is a snapshot of my change. Also, I notice that your matrix brackets look different than mine (while yours are continuous mine are segmented) does this signify something in MathCAD?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
V is a function of x, in the plot for the vertical axis you should type V(x) instead of just V.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Were you able to get the graph to populate? I tried adding in the V(x) rather than just V and it still has an error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What does it say?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The error on the V(x) in the plot says "This variable is undefined. Check that the label is set correctly"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And.... did you check the label?
Are the labels of the V as a result of Odesolve and the V in your plot labelled the same?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc, thanks again for all the help you are giving.
The V is indeed a V.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So does it show a graph now?