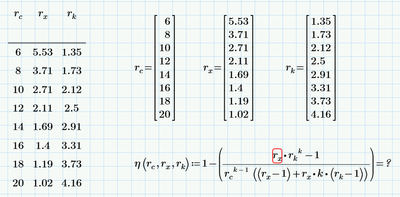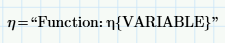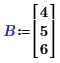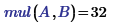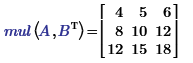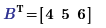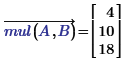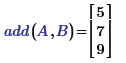Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving for values in a table
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving for values in a table
Would love help with this. I've defined my function, inserted a table of values, and am expecting results in a vector format.
HELP!!
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ahhh, thanks a ton! This worked! Next is to figure out how to plot!
Thanks a bunch.
M
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please attach the Prime worksheet, not just/only a picture.
Some upfront advice:
1. Make sure that k is defined.
2. Vectorize the expression at the right-hand side of the definition.
3. DON'T evaluate a definition. That is: do NOT put an '=' at the end of a definition. It may work in many cases, but in ever so many cases it leads to problems. Use a separate region to evaluate your expression.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have to delete the equal sign after the function definition and evaluate the function in a separate region.
Furthermore I guess you will have to vectorize the function call as you will get wrong results otherwise.
I second what Luc already said - attach the worksheet!
EDIT: Ahh, I see that in the meanwhile Luc has edited his reply and suggests quite the same 😉
Another option would be that you don't define a function but a simple variable eta:=...
In this case you would have to use vectorization as well but you could use inline evaluation (the = after the definition). But for some reason inline evaluations have proven to be instable in some situations and so I suggest not using it.
BTW, inline evaluation never works when defining a function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
File attached....
I am really new at this so I appreciate the patience...
When you say "vectorize" the function, how is that accomplished?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Whoops, sorry, I was working on a different computer and the file did not save. I'll upload revised shortly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
vectorizing is the operator which shows as an arrow over the expression:
You may note that you can define the function above the table with values. They need not to be defined when you define your function.
So I would suggest to either define a function beforehand and the call it vectorized and assign the result to a variable or simply assign the definition (which is less preferable in my opinion).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ahhh, thanks a ton! This worked! Next is to figure out how to plot!
Thanks a bunch.
M
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have edited my reply and attached the work sheet
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
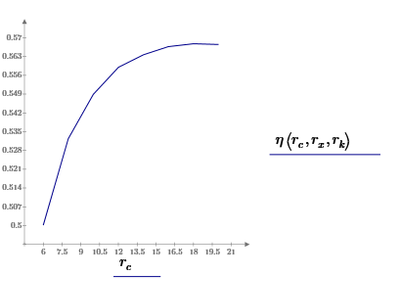
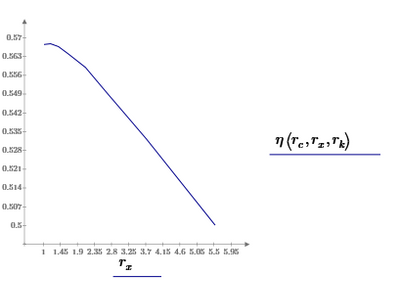
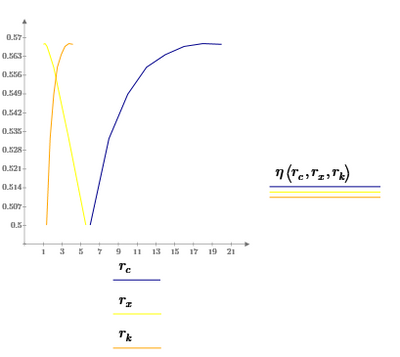
How to plot...
Assuming you'd want to plot the eta results, you'll have to decide what you want to plot it against:
r_c?
or r_x?
or all three?
success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
vectorizing is the operator which shows as an arrow over the expression:
You may note that you can define the function above the table with values. They need not to be defined when you define your function.
So I would suggest to either define a function beforehand and the call it vectorized and assign the result to a variable or simply assign the definition (which is less preferable in my opinion).
I'd have been tempted to put the vectorize operator inside the function.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Add two statements:
You've defined a function, which is what Prime is saying with the statement
So you can define a variable (N) to evaluate each occurrance of the r_c, r_x, and r_k (which is what the "vectorization" (the arrow above the function) does, and then you can see each N. (Which is what Luc and Werner were saying.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think i understand now. if the variable is in a vector format, then the resulting equation or function must also be in a vector format...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"if the variable is in a vector format, then the resulting equation or function must also be in a vector format"
Often, but not necessarily. You can write a function
that accepts two vectors
and results in a single number,
or in a matrix
(Note that
)
But if you use vectors to hold sets of values that you want to operate on as sets, like you do here, you mostly need to vectorise the expression.
and beware. The function:
supplied with the same variables, results in respectively:

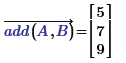
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@MH_10178519 wrote:
I think i understand now. if the variable is in a vector format, then the resulting equation or function must also be in a vector format...
Just to amplify the point others have made, it's the nature of the vector operations that determine whether you need to vectorize a result. Mathcad operators and functions generally have a vector/matrix interpretation if there is one, otherwise they will either raise an error or apply to each element of a vector/matrix. For example, look at the difference between the outputs of vector dot product(*), matrix multiplication, vector power, vectorized multiplication and the sine function.
Consequently, you only need to apply vectorization when you intend the operation to be element-by-element.
Stuart
(*) The dot product produces a scalar. [1xn] * [nx1] matrix multiplication produces a [1x1] matrix.