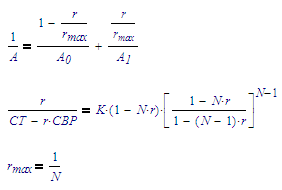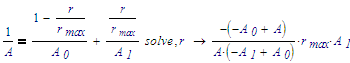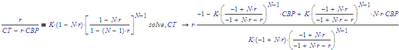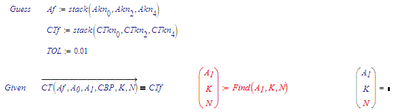Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving numerically one equation and data fit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving numerically one equation and data fit
Hello Everyone,
I have some experimental points, and I need to fit this with a equation. But the dependence of variables is related wtih a second equation. The problem is explained in the attached file.
Can somebody help me?
Thanks
- Labels:
-
Other
-
Physics
-
Programming
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
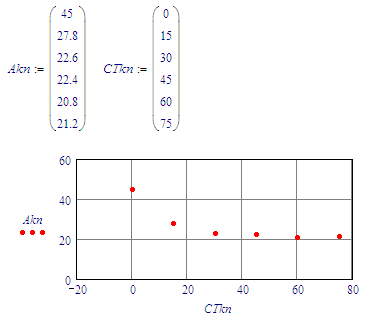
Let's establish that the following is known:
Furthermore these equations are given:
Using the first, we can write A as a function of r:
but we can also write r as a function of A:
And that is much more useful, because we cannot write r as a function of CT, but CT as a function of r solves as:
Using this we can substitute r with its function of A, and substitute the third function as well:
So now we have a function CT(A, A0, A1, CBP, K, N).
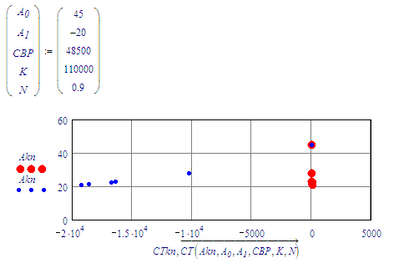
If the supposed solution is entered, and compared to the known points, we get:
The 'solution' is nowhere near the known points (except for CT=0).
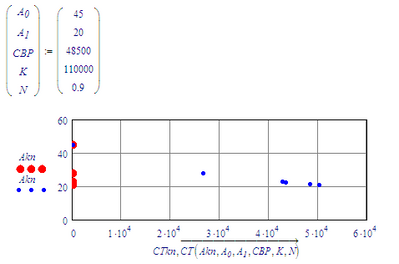
Let's see if we can get a better approximation:
That's more like it.
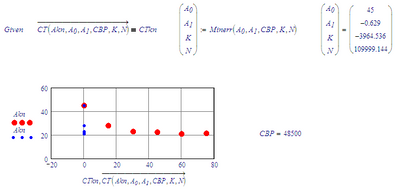
With these results as guess values, one more try:
I hope this brings you further.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As far as I understand it, is CBP not a value to solve for but should be of constant value 48500.
And the supposed value for A1 is not -20, but should be around +20.
You may consider using a solve block function (or using the root command) to create a function r(CT,K,N) and use this function with equation (1) in a solve block with minerr(K,N,A1).
But I am not sure that the problem is well conditioned.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"the supposed value for A1 is not -20, but should be around +20"
OK then:
And with these values as guess values I get:
Re-iterating once more causes only minor shifts of the values.
Keeping CBP fixed at 48500:
And another iteration gives:
"I am not sure that the problem is well conditioned". I fully agree.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner_E,
Exactaly, CBP must be 48500 and A0 must be 45. I don't know how to use solve block function. I'm trying to use the tips of LucMeekes to solve the problem.
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@M_U wrote:
I don't know how to use solve block function.
This is what I had in mind:
The solve block will use your equation #2 to calculate the r-value if you provide CT, K and N.
You could then set up a second solve block using equation #1 to get the optimized values for A0, K and N.
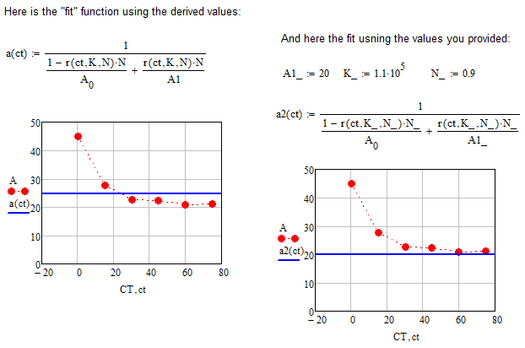
But as you can see in the picture above, the value of "r" are VERY similar, no matter which value of CT you provide (I used the values for K and N you wrote that Matlab had come up with).
This would mean, that the values of A from the second solve block also would be very similar and this would result in a more or less horizontal line - not what I would call a good fit!
So the question is if you are absolutely sure about the equations and values you provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For completeness sake here is the second solve block
and here is the "fit" function, which sure doesn't deserve that name
As already written in the file, the results are in no way reliable as they depend heavily on the chosen guess values.
MC15 worksheet is attached in case you'd like to play around with it anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner_E,
I tried to use your tips but unfortunately I couldn't solve my problem. Anyway thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi LucMeekes,
A0 e CBP must be constants, in this case, A0 = 45 and CBP = 48500. The value of A1 must be positive around 20.
I'm using your tips to try to solve the problem. I'm starting to work on Mathcad and I think it will take a while to test.
Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Assuming you're using Mathcad (15, not any version of Prime), a solve block looks like this:
It starts with the word "Given", then a number of equations, and then one of the solver functions. Note that there are 6 equations, all due to that single statement with an arrow above it. Essentially the CT function is applied to each of the elements of the Akn array, and compared with the associated value in the CTkn array. In the above case the solver function used is 'Minerr' which tries to find the value for each of its arguments such that the error in the equations is minimal. (Look it up in the online help, if you need more information. Also it helps to learn if you build the examples of the online help yourself, to get familiarized).
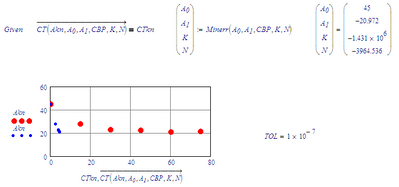
Another solver function that you may want to try is 'Find', but that requires that you have as many equations as there are variables to solve for. With your statement that CBP and A0 are constants, I removed them. That leaves 3 variables to solve for, so only 3 equations can be used. I built another set of known value arrays for A and CT (taking the 1st, 3rd and 5th elements, note that element addressing starts at 0 by default). With that, now this happens:
The find function turns red, indicating an error. The error is: "No solution was found". Either the guess values are too far off (they're set to the supposed solution values), or the tolerance is set too tight (well, it is set at 0.01, which is 10 times its default).
My guess is that either I made a mistake in entering your formulae, or your formulae do NOT properly model the process.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi LucMeekes,
I tried to use your tips but unfortunately I couldn't solve my problem. Anyway thank you.