Sometimes multiplication is really complex ...

[StuartBruff]

Every engineer, mathematician and scientist is born knowing that the vector dot product is the sum of the element-by-element multiplication of the components of the two vectors. But occasionally, when our brain isn't paying full attention, things don't work out as intended ...

Stuart

PS.  I blame Valery for this one.  If he hadn't posed that clock question, I wouldn't have tried to generalize it and spend a couple of minutes wondering why my previously fine power series expansion formula wasn't working when applied to complex number bases.

[AlanStevens]

An interesting bug!  It appears that Mathcad takes the complex conjugate of the "z" vector before multiplying!  You can avoid the problem by replacing a*z in PowerDot Mul by aT*z  (where aT is the transpose of a).  Mathcad no longer bothers to take the complex conjugate!

Alan

[StuartBruff]

AlanStevens wrote:

An interesting bug!  It appears that Mathcad takes the complex conjugate of the "z" vector before multiplying!  You can avoid the problem by replacing a*z in PowerDot Mul by aT*z  (where aT is the transpose of a).  Mathcad no longer bothers to take the complex conjugate!

Interesting.  A bug?

Stuart

[lturek]

Thats not a bug, thats exactly how the dot product is defined for complex vectors in math

and Mathcad knows about that definition

So if you just want the summation of elementwise multiplication, you should use the matrix product a^T*z as Alan had pointed out

For real vectors there is no difference between the two (as every real is its own conjugate)

[StuartBruff]

Leopold Turek wrote:

Thats not a bug, thats exactly how the dot product is defined for complex vectors in math

and Mathcad knows about that definition

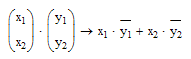
Indeed.  It even says so in the Help for the dot product:

• If x and y are vectors, returns the dot product (inner product) of x and y, a scalar formed by multiplying element-wise the entries of the first vector with the complex conjugate of the entries of the second vector, and summing the results.

However,

Thats not a bug, thats exactly how the dot product is defined for complex vectors in math

In quantum theory, the bra-ket notation ⟨v|w⟩ defines the inner product as being the conjugate of the first term rather than the second term, ie the result is v^*·w

, where ^* denotes the conjugate transpose.

Interestingly, and confusingly, Mathematica defines Dot[v,w] as the Hademard (element-by-element) product whilst Matlab and Maxima take the braket approach in conjugating the first vector.  Python's numpy library adopts two approaches, with dot carrying out Hademard multiplication and vdot multiplying braket style.

Stuart

[lturek]

StuartBruff wrote:

In quantum theory, the bra-ket notation ⟨v|w⟩ defines the inner product as being the conjugate of the first term rather than the second term, ie the result is v^*·w

, where ^* denotes the conjugate transpose.

This would be conform with Matlab and Maxima. It serves the same purpose as if we conjugate the second vector - the inner product of a vector with itself would be always positive.

However until now I was only aware of the definition Mathcad is following (transpose the first but conjugate the second vector) - just looked it up in some books.

I always found the same definition as given by Wiki https://en.wikipedia.org/wiki/Dot_product#Complex_vectors or Wolfram http://mathworld.wolfram.com/HermitianInnerProduct.html

Interestingly, and confusingly, Mathematica defines Dot[v,w] as the Hademard (element-by-element) product 

I am not well versed with Mathematica, but maybe it distinguishes between the Hermitian Inner product (see reference above) and a simpler Dot Product Dot Product -- from Wolfram MathWorld

Confusing anyway.

LT