Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
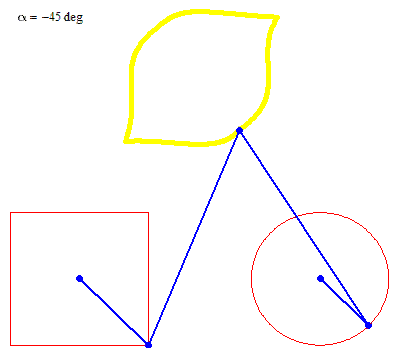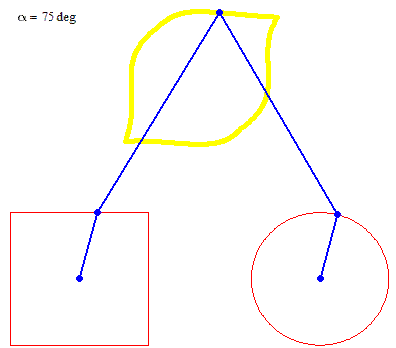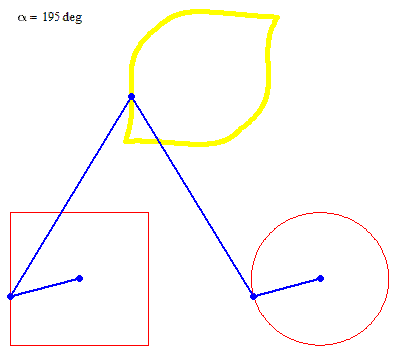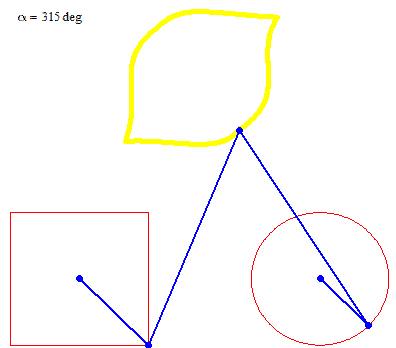
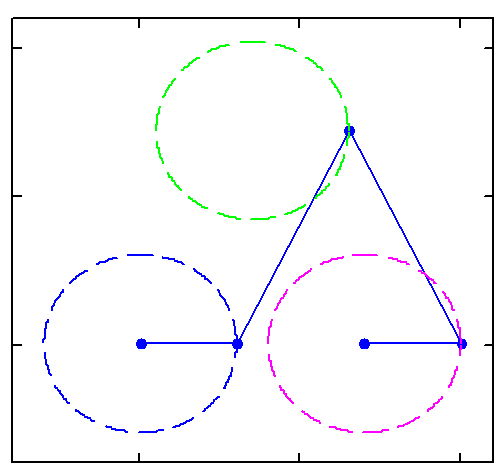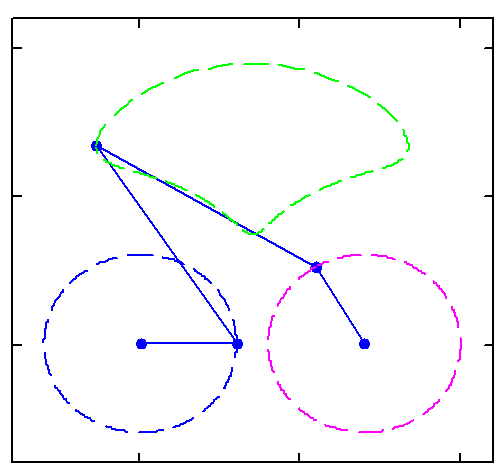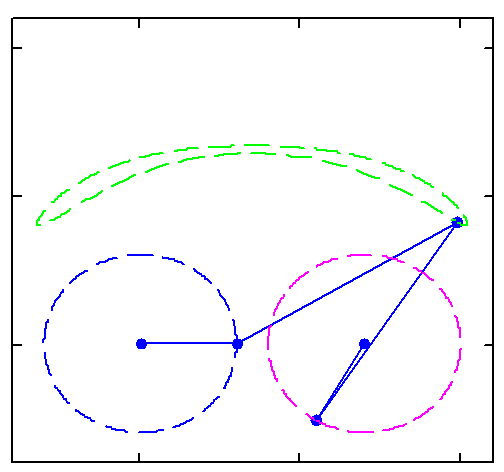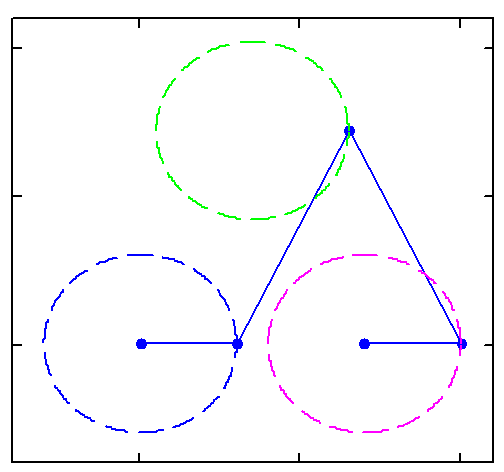
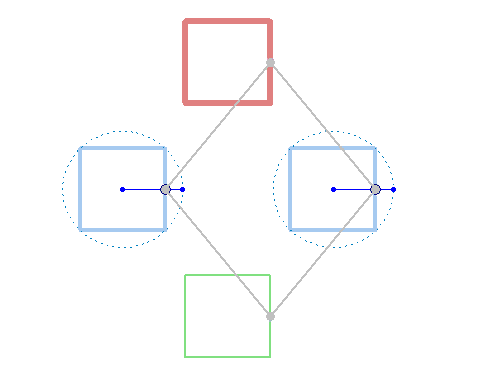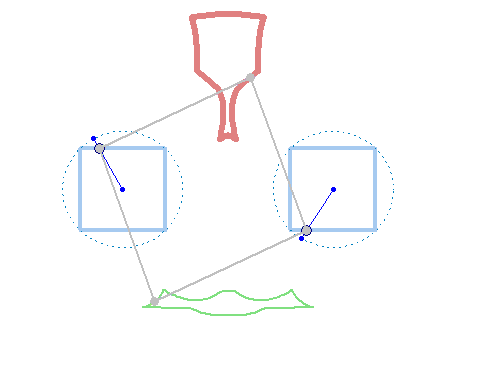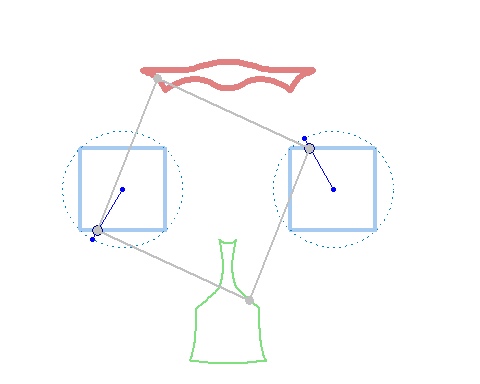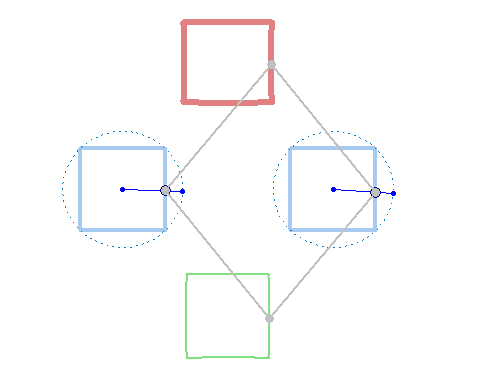
Square + circle = lemon
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Square + circle = lemon
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
....limoncello....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
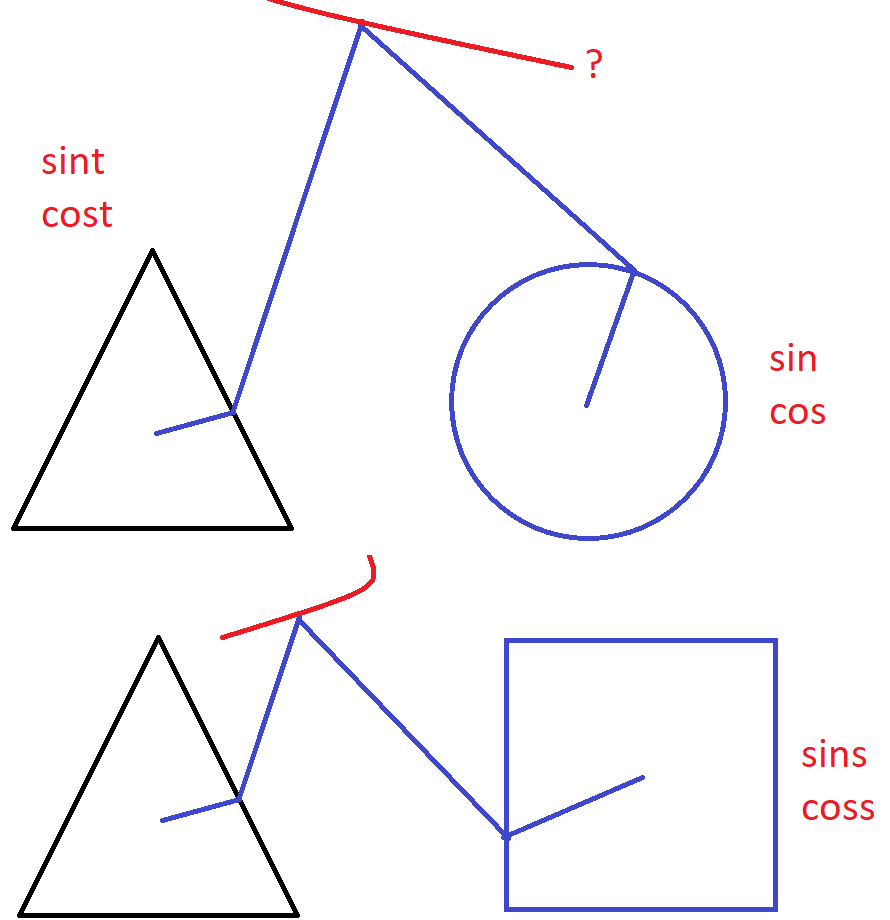
There are sin, cos etc
There are sinh, cosh etc (hyperbolic)
But we need sins, coss (square), sint, cost (triangle)!
Can you help me to create this animations?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The origin of the animation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Undoubtedly it is an interesting topic, but, I'm sorry, I can not, I'm already busy with other jobs.
Greetings
FM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
Hi,
Undoubtedly it is an interesting topic, but, I'm sorry, I can not, I'm already busy with other jobs.
Greetings
FM
Hi,
Undoubtedly it is an interesting topic, but, I'm sorry, I can not, I'm already busy with other jobs.
Greetings
Val
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
@-MFra- wrote:
Hi,
Undoubtedly it is an interesting topic, but, I'm sorry, I can not, I'm already busy with other jobs.
Greetings
FMHi,
Undoubtedly it is an interesting topic, but, I'm sorry, I can not, I'm already busy with other jobs.
GreetingsVal
Hmmm ? Must we be afraid nowadays to simply say "me too" ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
There are sin, cos etc
There are sinh, cosh etc (hyperbolic)
But we need sins, coss (square), sint, cost (triangle)!
Can you help me to create this animations?
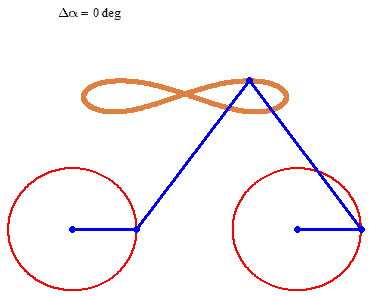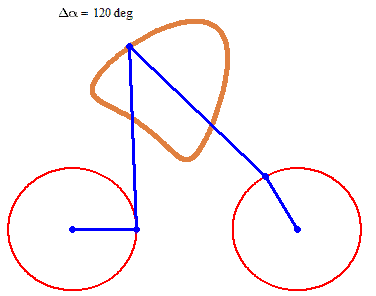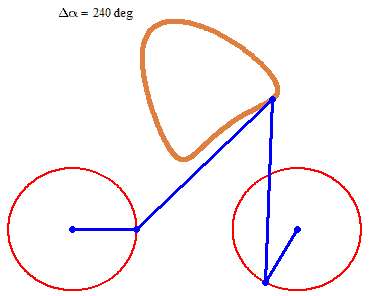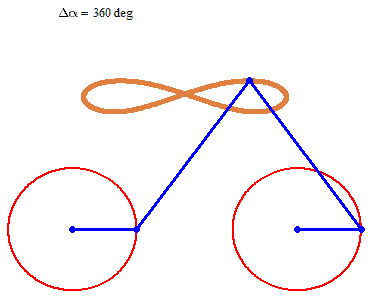
We sure don't need any sins or sint functions 🙂
Are you really looking for something like this?
No lemon, but maybe you can try to play around to get a decent Batman symbol
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
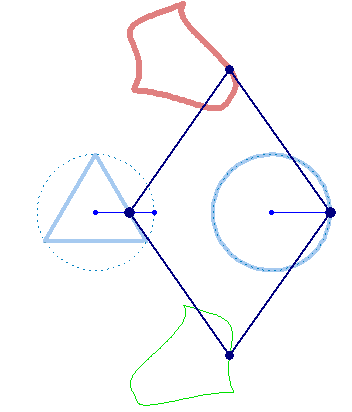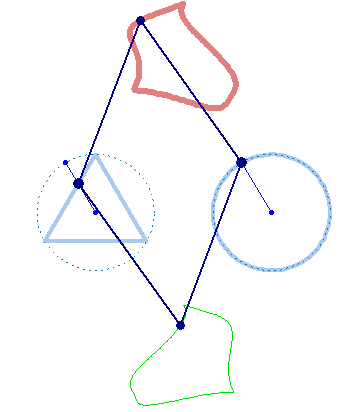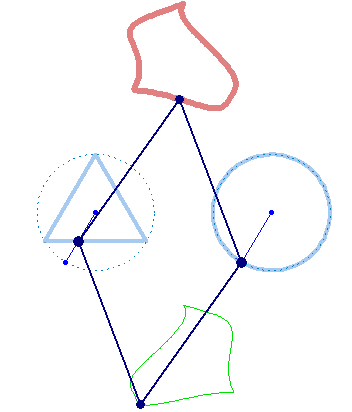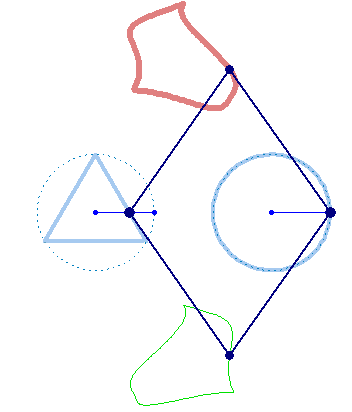
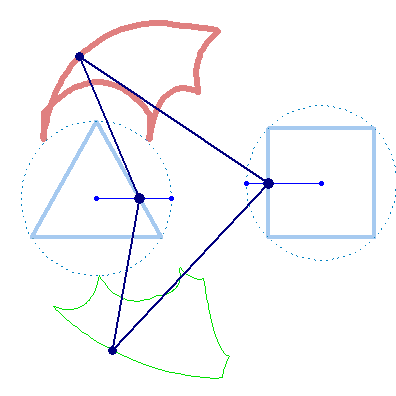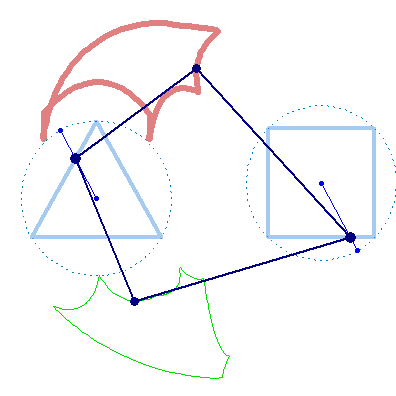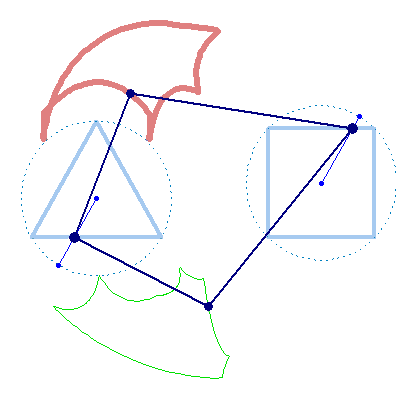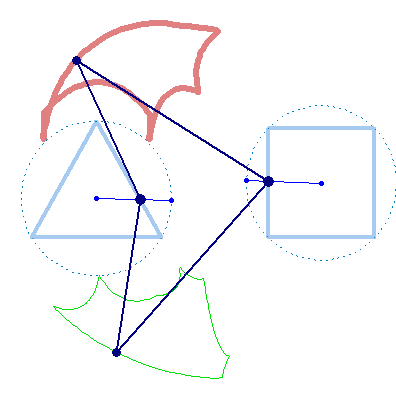
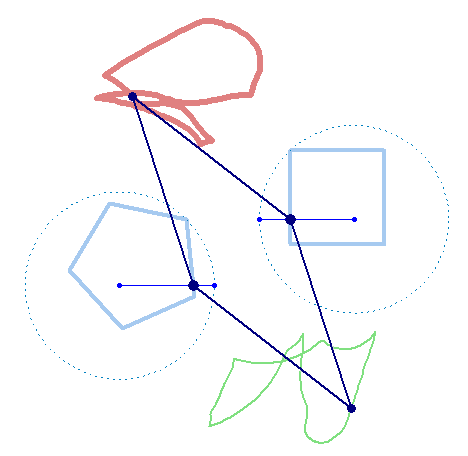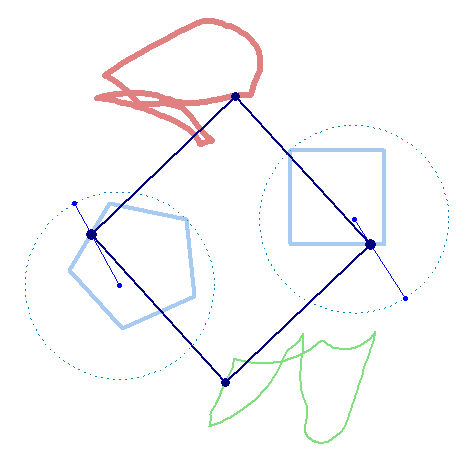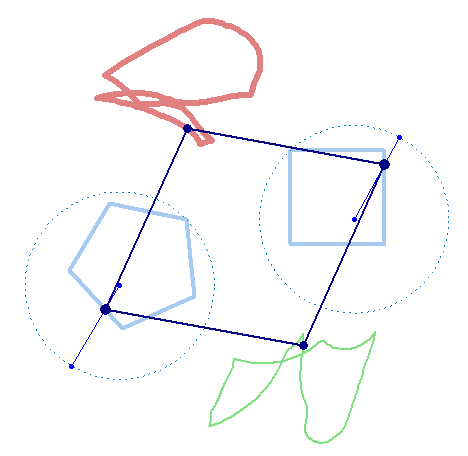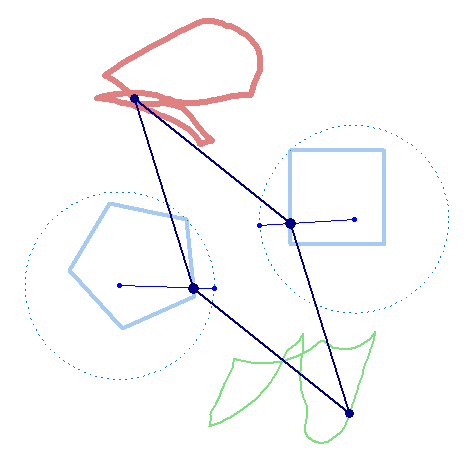
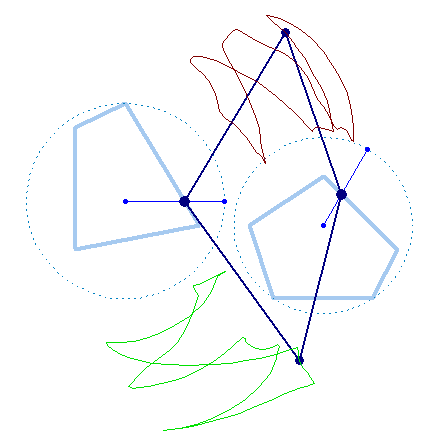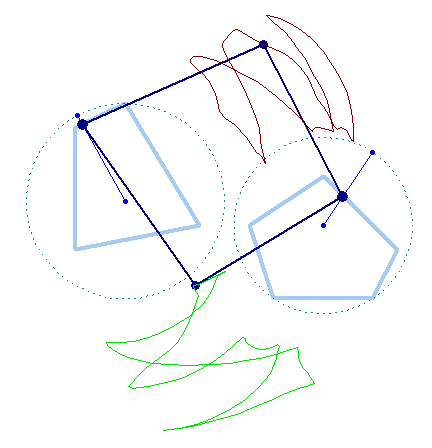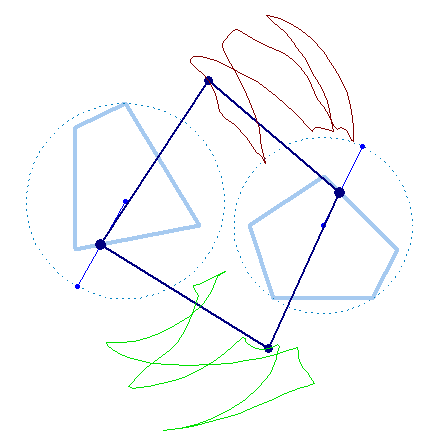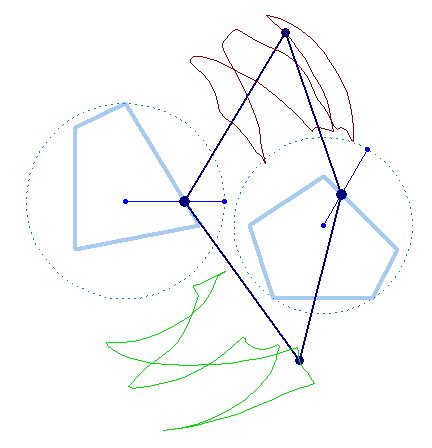
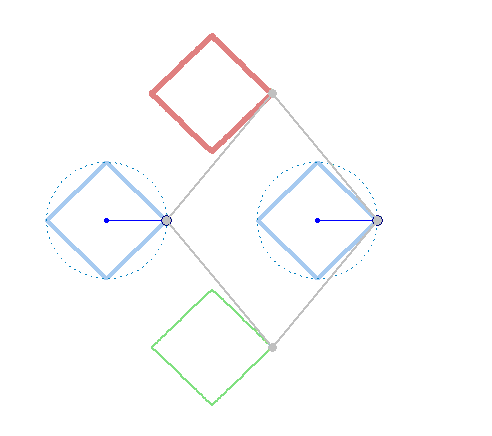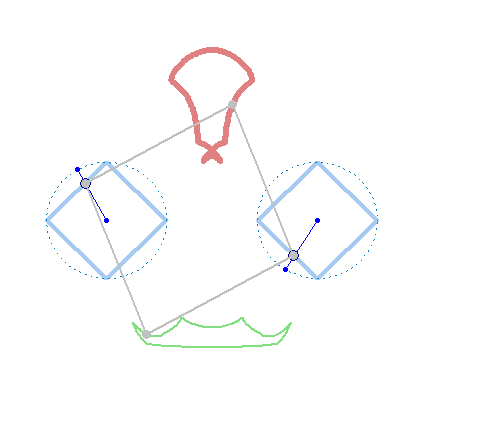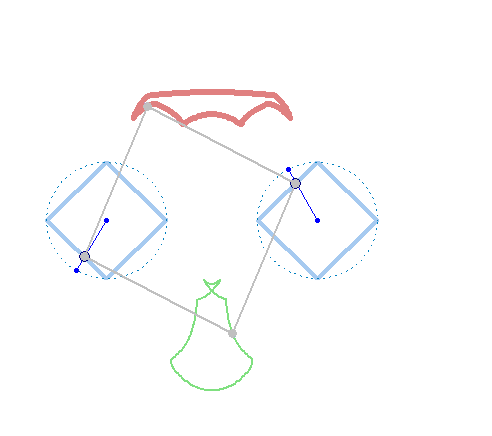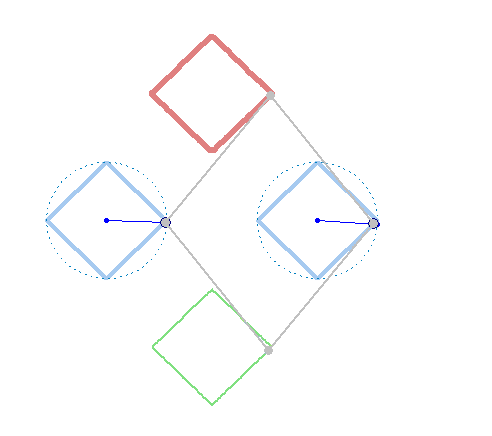
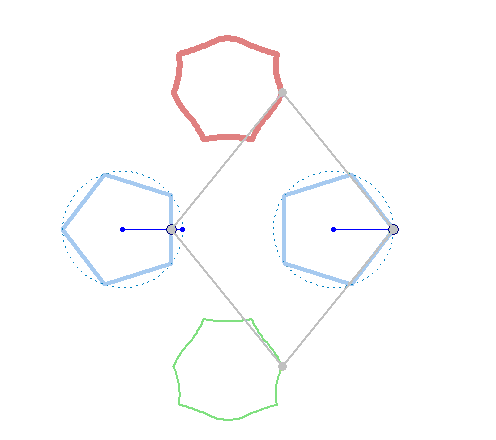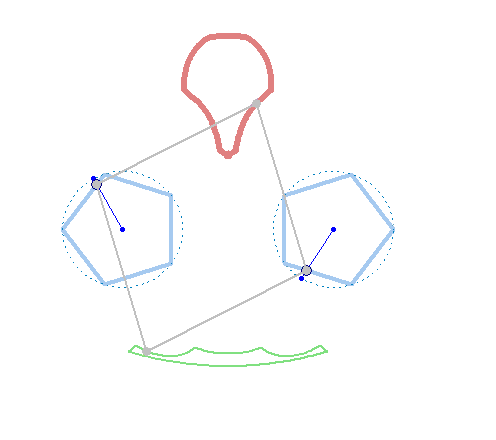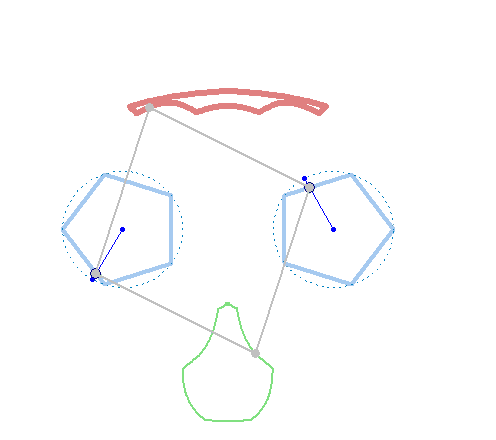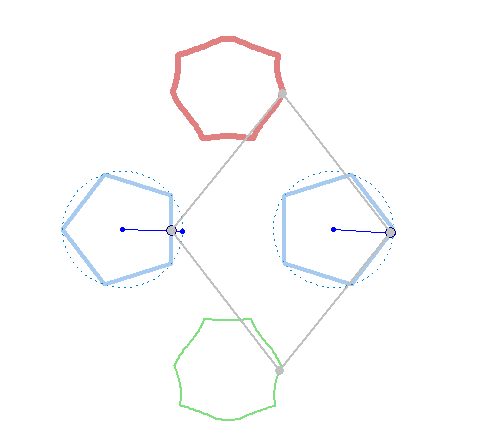
But rotation of the two must not necessarily be of the same speed:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
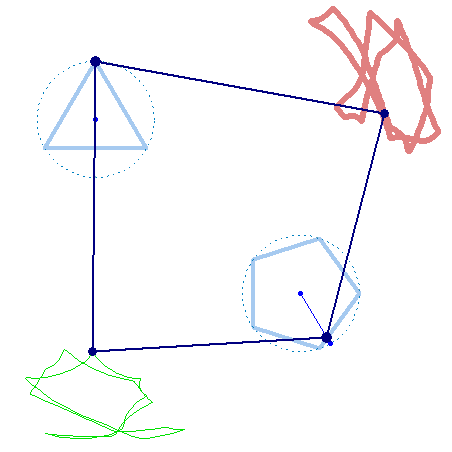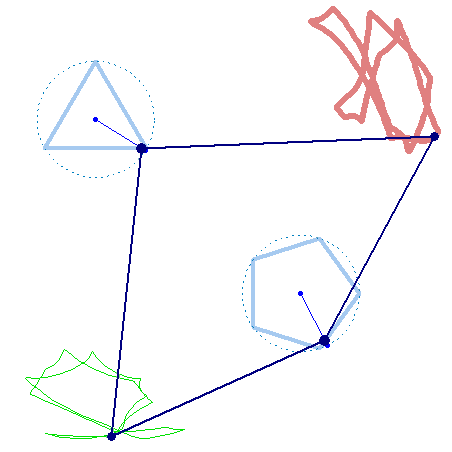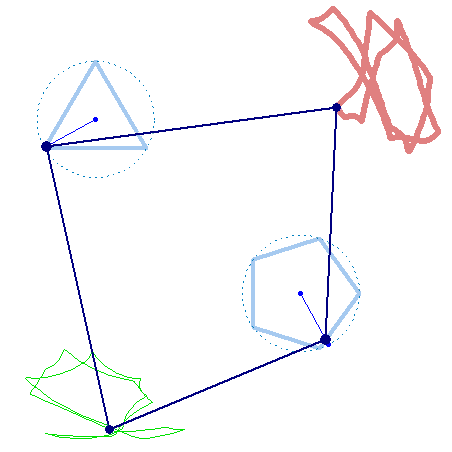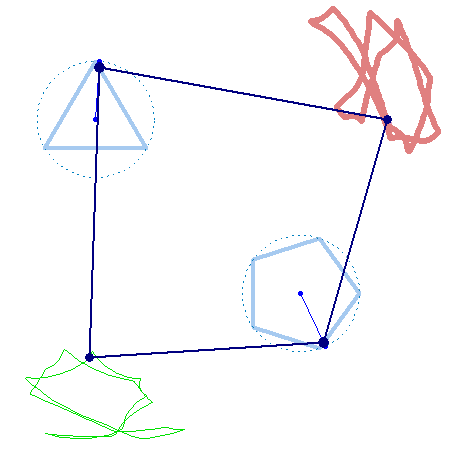
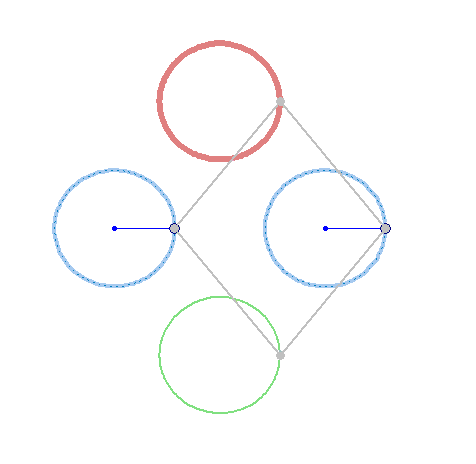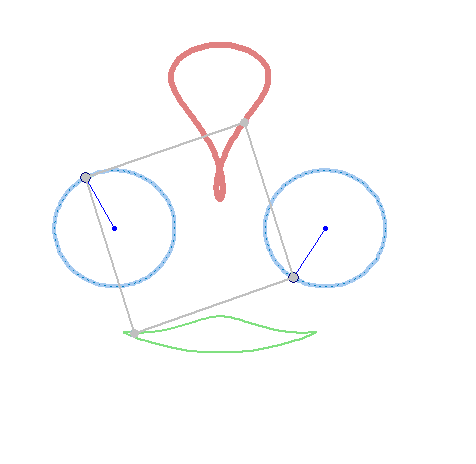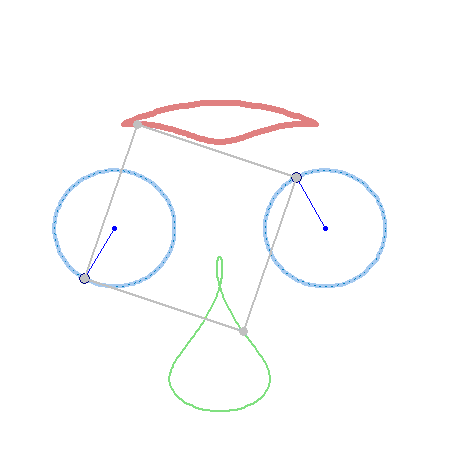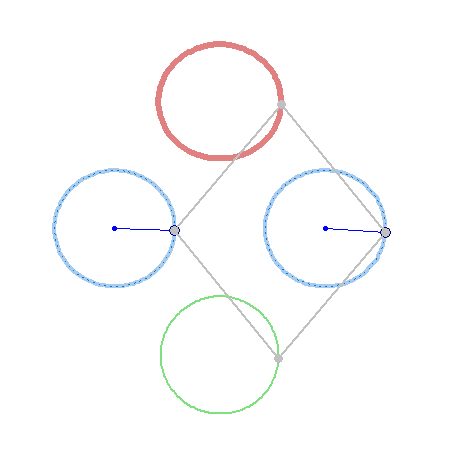
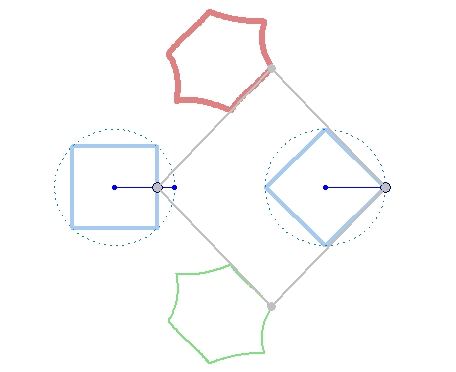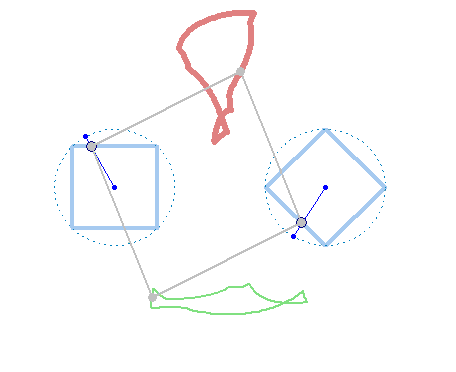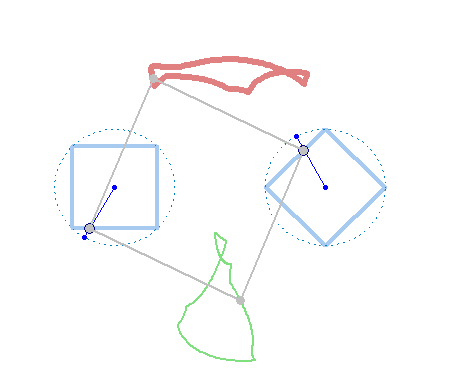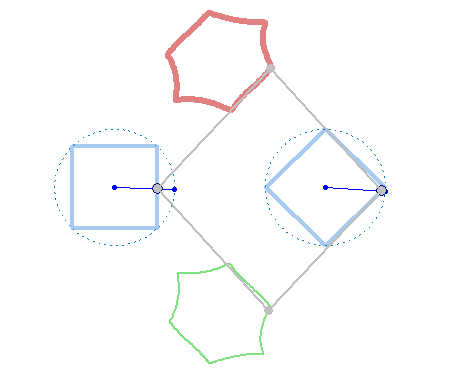
And furthermore the rotation must not be counter clockwise for both and the center of rotation must not necessarily be the center of the regular polygon:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And at last, we don't have to use regular polygons at all:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
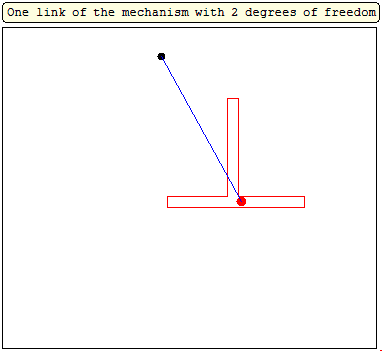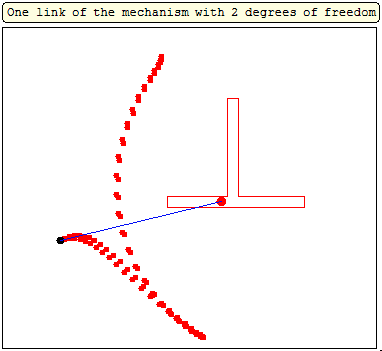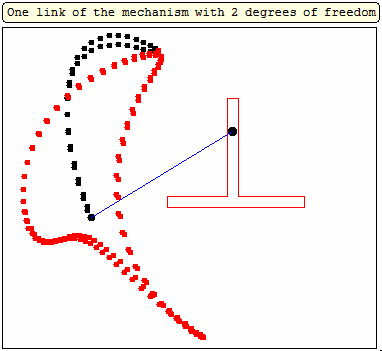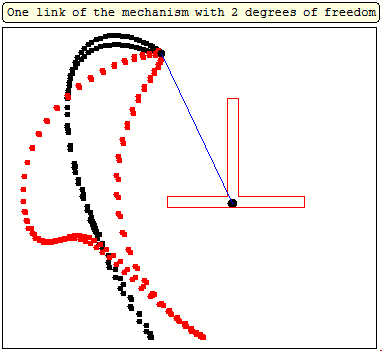
In the" unusual" mechanism of Verner two hinges of the hinged quadrilateral
move along the sides of two polygons, and the other two draw graphs. I also want to show the "unusual" (cam mechanism) made in Smath Studio.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Today in Russia, a day off is a women's day. We have almost no women at the forum, alas. But my congratulations are also my congratulations!
Я поздравляю всех наших дам с 8 марта.
Мое поздравление математическое!
При создании этой анимации пришлось решать систему нелинейных алгебраических уравнений.
Женщинам тоже приходится решать много житейских уравнений - дома, на работе, с подругами, с друзьями...
А уравнение - это некий баланс, равновесие, лад, учет своих и чужих интересов, прав и обязанностей...
Пожелаем же нашим милым дамам чувства баланса, равновесия лада... Без этого счастливая жизнь невозможна.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more fine animation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
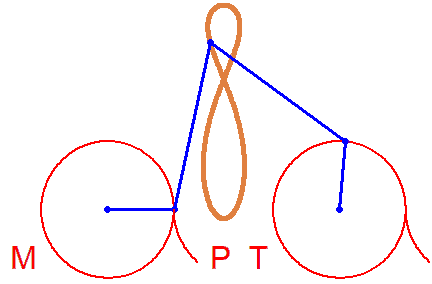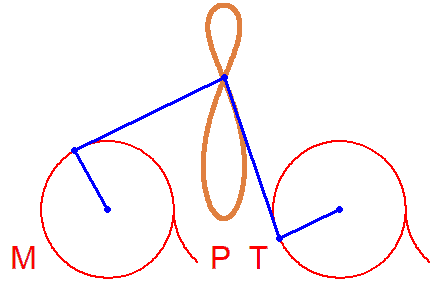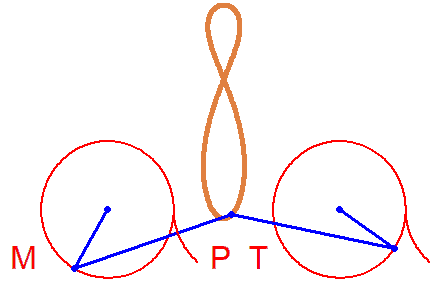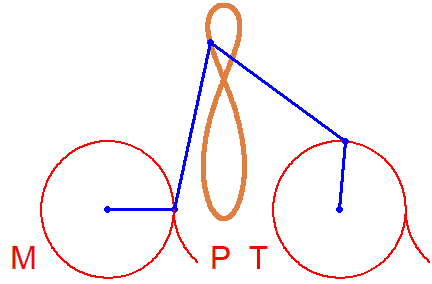
Fine too... A Bike. But rotations in different directions...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here are a few more.
With a little imagination you can see a clown face here and there.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And here's the rest of it
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
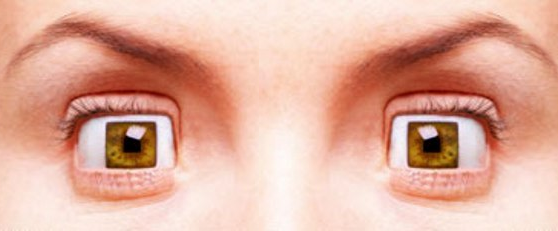
Thank you, Werner.
I woke up in the morning, looked and my eyes became square from wailing and admiration ...
PS
He looked at me with square eyes = He was very surprised when he heard from me this news.
Глаз правильный квадрат на пустой голове
Не отражается в них ни пряник ни плеть
Они открыты просто так им все равно куда смотреть
И фонари умных слов светят там и тут - зря! - там и тут
Они как окна домов люди в них не живут
Нет! нет! ты слеп!
Nautilus Pompilius - Квадратные Глаза
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is a triangle, there is a quadrangle (a square for example), there is a polygon, there is an... infiniteangle (a circle or an ellipse), and there is... a twoangle:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But now I am going to do so!
The weather in Moscow is fine for it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
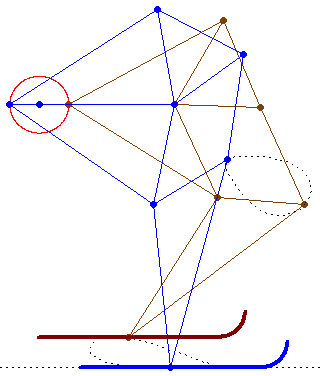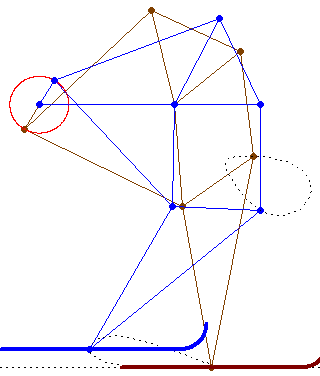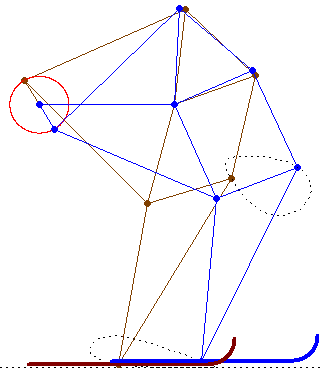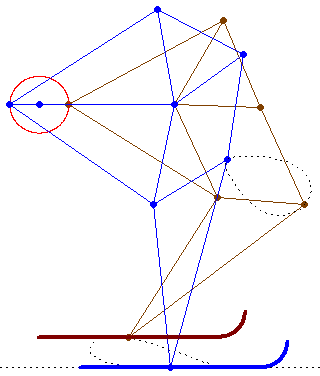
The sky run was fine!
But I thought not about the fine weather, not about the optimal temperature for sky (minus 7 grad), not about...
But about how many links, knots, traces of knots has this SnowLineMakersMachine (one German word for Werner) haben?
Can we draw all of them?
Help us Werner and all!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First but not main part
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more main but not quit correct (not steam but gas) part
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But about how many links, knots, traces of knots has this SnowLineMakersMachine (one German word for Werner) haben?
Guess its called a snowcat or a snow groomer (in german: Pistenraupe)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
But about how many links, knots, traces of knots has this SnowLineMakersMachine (one German word for Werner) haben?
Guess its called a snowcat or a snow groomer (in german: Pistenraupe)
See please
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner!
Send me please your cost, sint, coss and sins functions!
I would like to compare its with my ones!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Fridel!
But sorry!
It is not SMath but Mathcad forum.
One my student can create in C++ very interesting animation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Werner!
Send me please your cost, sint, coss and sins functions!
As already written we don't need such functions.
I simply let a beam rotate with constant velocity and calculate the intersection with all segments of the guidance polygon and use the one nearest to the center of rotation. While being pretty inefficient it calculates quick enough and so I can use whatever kind of odd polygon I want. There are a lot of restrictions at the moment, though. Center has to be inside the polygon but no error check is done. And it does not work well for non-convex polygons as I forgot to check if the point of intersection lies within the linesegment or outside. It was just a quick hack anyway.
Maybe some day I correct those flaws and post the cleaned up sheet here.