Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Stability of Offshore Platform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Stability of Offshore Platform
Hello all,
Tonight I am attempting the below problem:
The given correct answer is given as 14.49m for the centre of gravity from the keel of the platform i.e. KG=14.49m
I have so far approached this as follows:
I.e. the transverse Gravity to the Metacentre is equal to the Keel to the centre of Buoyancy + Centre of Buoyancy to the transverse Metacentre - KG.
I.e. KG=KB+BMT-GMT
I have also worked on the assumption that:
i.e. BMT is equal to the transverse second moment of the water plane divided by the underwater volume. I've also assumed that the KB is half the draft.
Further I have assumed that as the cylindrical columns are at the waterplane, the second moment of these areas will be about a circle and can be calculated as:
i.e. Pi * diameter to the power of 4/64.
I have carried on as below.
I think that I have calculated the underwater volume correctly and the second moment for one column correctly. I am not sure how to equate the total second moment for the total waterplane i.e. all 8 columns. I am sure it is not as simple as multiplying by 8 as I have done?
Further, I believe that if KB is actually T/2, then BMT would need to be a negative value which is unlikely for the metacentre to be beneath the centre of buoyancy as the metacentre is essentially the point at which the structure will rotate about when heeling either way. In fact the more I think about it the more I believe this must be impossible. So perhaps the KB value needs to be obtained another way than by assuming it is at half the draft?
Any help warmly welcomed.
Cheers,
Andy
Solved! Go to Solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
is it a dynamic problem?
If it's a dynamic process, when the platform rotates around the longitudinal axis.
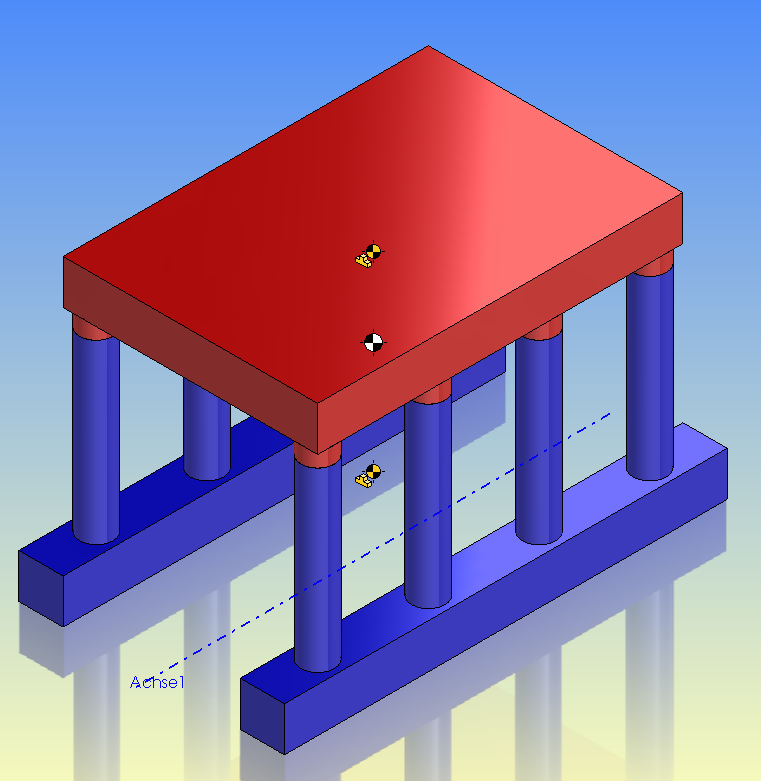
If you don't have all important measurements, how will you calculate it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I believe there is sufficient information to address the problem of "transverse rotation," i. e., roll, rotation about "Achse 1".
There is not enough information to address "longitudinal rotation," or pitching
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think it is a dynamic problem. I think it is a static stability problem i.e. to calculate the loading to give a GMt (distance from COG to transverse metacentre) for initial stability.
- « Previous
-
- 1
- 2
- Next »





