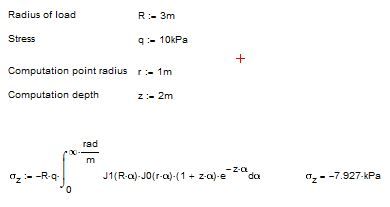Stress below circular loading

[TikkaMasala]

Hello

I'm trying to compute the stress under circular load (not only below center line, but below any point).

I have found the attached article about the topic, but I wasn't able to make the computation indicated in formula 3c. The units doesn't seem to match. (http://onlinepubs.trb.org/Onlinepubs/hrr/1963/39/39-004.pdf)

I have found an old mathcad computation sheet about the problem, but the reference to these formulas is unclear.

The attached sheet includes some of my tries to solve this problem based on the attached article.

But my feeling is that I'm not even close...

Thank you for your help in advance.

[LucMeekes · Accepted solution]

Is this what you are looking for:

Success!
Luc

[TikkaMasala]

Thank you for your quick answer.

With this change you proposed the computational stress values seem to match with the 

older mathcad sheet, which was as attached in that zip file.

Could you, or someone else, explain why the infinity is divided with meters?

I mean, yes the result is apparently correct, but the reason for strange unit 1/m for the upper and lower

integral limit is unclear to me...

[Fred_Kohlhepp]

Mathcad requires "unit balance".  The integral terms consist of terms in the form R times alpha.  R you have given the dimension meters, but R times alpha needs to be unitless or the Bessel functions won't evaluate.  So, giving alpha the units of 1/meters allowed the program to evaluate.  (It was genius!)

[MJG]

Note that you can use any unit of length since the following are true:

0m = 0cm = 0ft = etc...

∞m = ∞cm = ∞ft = etc...

Or rather, in the example given, these equalities are more applicable:

0/m = 0/cm = 0/ft = etc...

∞/m = ∞/cm = ∞/ft = etc...

[TikkaMasala]

Thanks for the comments and guidances.

As the integration formula are done to evaluate stress distribution under axisymmetric loading,

could it be that the "more correct" integration limit is infinity with units [rad/m].

The resulting stress of course remainst the same as with [1/m].

[LucMeekes]

Yes it could.
Be sure that the unit rad is defined as 1 ( unitless)

Success!
Luc

[TikkaMasala]

Yes, I agree

So the formula becomes as follows:

[LucMeekes]

Yes,

note that physically/mathematically this is incorrect, because also the lower limit of integration has a unit, and must have the same unit as thye upper limit.

However mathcad is a bit forgiving in that it will apply the correct unit to any 0 it finds/needs.

Luc