Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Stumped Help Please
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Stumped Help Please
I have a problem in mathcad I do this problem -(100ohms/50ohms)tan^-1= Now when I try to add a degree sign at the end it errors out. I have done this problem and know it works however when trying to do it again this happens. I noticed the only difference between the one that works (formula) and the one that doesn't there is a shaded out box before the degree sign (one that doesn't work) I have tried to delete it no go. Any suggestions?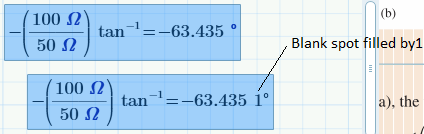
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> I have a problem in mathcad I do this problem -(100ohms/50ohms)tan^-1=
Thats no correct mathematical expression (unless tan is a scalar an not the trig function).
If tan^-1 should be the inverse function of tan, you should never call it tan^-1 (even though Mathematica does it and you probably see tan^-1 on your calculator) as it has a standardized name:- arctan. In Mathcad and Prime this function is called atan.
Prime for some unknown reason supports the usage of tan^-1 in combination with that strange postfix notation but I see no reason why this should be used.
To get the angle displayed in degree you can either type deg in the unit place holder, or type 1°(as you have done but it sure looks not good) or use the menu to insert the appropriate unit (unlike as in Mathcad 15 and below, in Prime the degree character unfortunately cannot be inserted simply via keyboard).

To conform with the standards you may (somewhere near the top of the sheet, maybe in a collpsed region) define a function arctan and use this

WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
What amazes me here is that the postfix notation actually works for all the built-in and user functions I have tried. I can't find any documentation on this.
Additionally, the tan^-1 notation works in postfix notation, but not in prefix notation.
Thinking back to how Mathcad 13-15 implemented affine temperature units with postfix operators, this postfix notation might have some interesting possibilities for user functions where it makes more sense, notationally, for the operator to follow the parameter. This is an interesting quirk that Scott has stumbled upon.
Jeff
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I wasn't amazed that postfix notation worked in Prime as I had noticed this before.
But I was amazed to see that some (it doesn't work with ln or log) inverse functions seem to be defined in two different ways and the notation with ^-1 can only be used as postfix. tan^-1 cannot be used the usual way.
As the inverse of the trig function should not be named that way (^-1) and the notation is simply wrong, I would call that a bug, not a feature 😉
Not sure what they had in mind when they implemented it.
While even a user defined function can be used in postfix notation, ....^-1 (of course) does not work with a user defined function (but that would be a nice feature 😉

Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner.
I don't have Prime right now, but can do this few comments: tan^-1 it's an usual notation for the the inverse of the tangent function but log^-1 isn't an "usual" notation for 10^x, nor ln^-1, etc. Those others are more likely a properties of the function, more than a definition of the inversion procedure. So, all red in your file are ok, that's for me. For the nice notation, you can use better the prefix operator, hope like in Mathcad 15.
Best regards.
Alvaro.
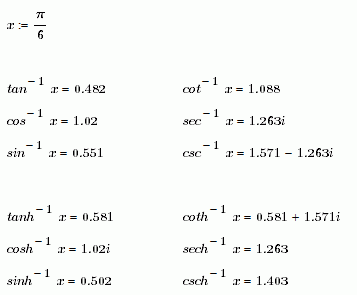
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know that sin^-1, etc. are quite common and wide spread notations.
But in my opinion it wrong to use it.
For two reasons and both have to do with the ISO standards (and also conforming national standards like DIN or ÖNORM in my area):
1) The standards define a name for the inverse functions of sin, etc. So this name (arcsin in my area, not sure about the current ISO; I think the former ISO said its asin) has to be used.
2) For funktions like sin, cos, etc there is a convenient shortcut when it comes to raising the function result to the n-th power. Instead of writing sin(x)^n we are allowed to write sin^n(x) or even sin^n x if x is a single and not a composite argument (I guess the latter short is also mentioned in the standards.
Writing the exponent directly after the function name and not after the closing argument parenthesis is not allowed for all functions, especially not for user defined functions like f(x):=..... We have to write f(x)^2 and not f^2(x).
There is a reason behind this and the reason is to avoid confusion about inverse function and reciprocal value.
f^-1(x) has to be the inverse function of f(x). It can't be anything else, because its not allowed to write an exponent before the argument parenthesis.
On the other hand with sin(x) we have the convenience to write sin^3(x) if we mean sin(x)^3 and sin^-2(x) if we mean 1/sin^(x)^2.
So what does sin^-1(x) mean. The inverse or the reciprocal value? Because of the aforementioned shortcut notation it has to be the reciprovcal value 1/sin(x). And this goes hand in hand with the fact, that the inverse of sin has its own name which must be used.
I know thats a tilt at windmills and the labeling of the keys on almost any pocket calculator or the fact, that even Wolfram uses sin^-1 for the inverse doesn't make it easier to convince people that they should not do so.
Of course I am aware that many (good quality) papers use the sin-^1 notation but nevertheless I can't help - its wrong in my opinion.
We have a similar problem with the use of "log". Log should be either used for a generic logarithm (when you write down rules which are valid for logarithms of any base) or you should provide a subscript to denote the base. If you mean log to base 10, you should (also according to the standards) write lg, if you mean the natural log you have to write ln.
There are so many publications out there, where log (without specifying a base) means either lg or ln. We see both in print and can only guess by the context, what the author means. Thats annoying and wrong, too.
Mathcad is no exception - it uses log for lg. This was a bit of surprise as I thought that in the English speaking area log is mostly used for ln. But maybe I was wrong in thinking that.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks so much for the alternative approaches to my problem! I will use these.
Peace,
Scott
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the confusion is caused by the option either of the function or the unit.
in this case you need the unit -
go to the "units" tab on the math page and under angle you have the choice of 2 different symbols for degrees or radians, steradians, revolutions or DMS.
the option on the operator tab allows the input of a number as degrees, but it will be converted to and stored as radians.
regards
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jeff,
As I read you reply, the duh kicked me. I am going to us my educational option, starting today.
Thanks.
Scott





