Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Sum of series. Symbolic vs numeric
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sum of series. Symbolic vs numeric
Why I'm getting different results for the sum in the attached worksheet with the symbolic and numeric evaluations ?
I think I've made somewhere a mistake..., but I cannot find where.
Probably I am so far not able to see the forest behind the tree...
Many thanks for help, Liv.
The worksheet was saved in Mcd11, but same results in Mcd15.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard.
Yes, it's not enough to make this difference.
Then the discrepancy is this other: using symbolic it's assumed that in a summative, the upper limit is biggest than the lower limit, but not in the numerical evaluation. The difference between both values (1/12) came from this, as it's showed in the attached. Also is the cause of the discrepancy identified by Fred.
Best regards.
Alvaro.
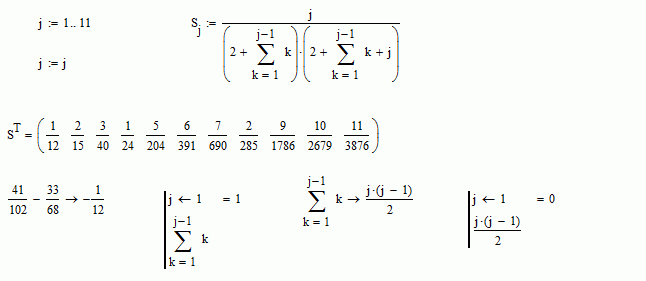
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Liviu.
It's just a round error. For example, if you modify the expression for the sumatorie, get a better numerical result, as is showed in the attached.
Best regards.
Alvaro.
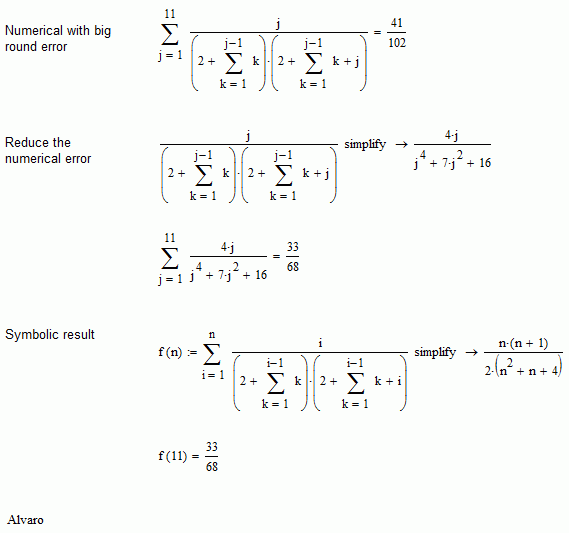
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure you are right. I don't believe this should have any significant numerical error:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The individual elements calculate correctly:
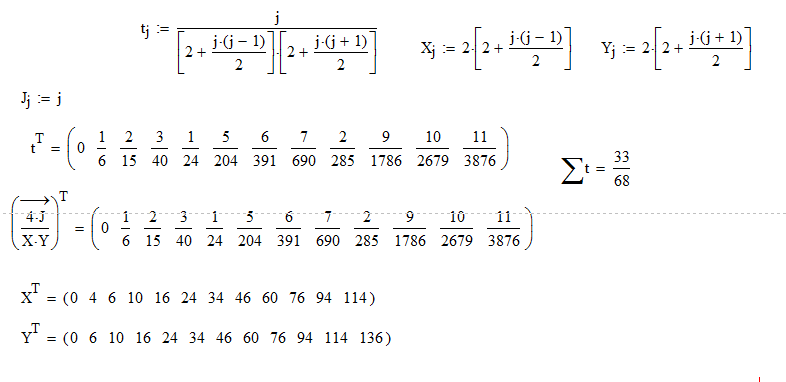
But the summations don't correlate:
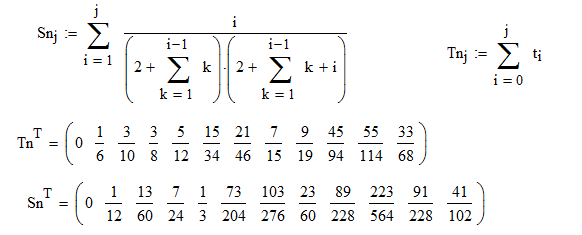
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard.
Yes, it's not enough to make this difference.
Then the discrepancy is this other: using symbolic it's assumed that in a summative, the upper limit is biggest than the lower limit, but not in the numerical evaluation. The difference between both values (1/12) came from this, as it's showed in the attached. Also is the cause of the discrepancy identified by Fred.
Best regards.
Alvaro.
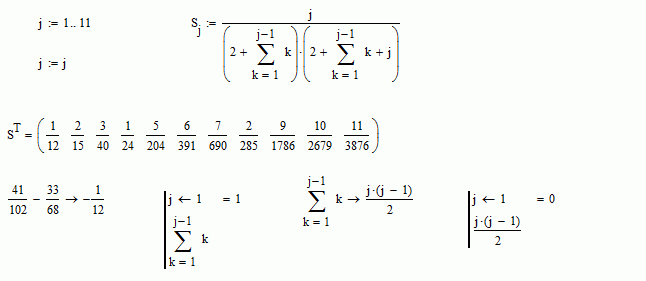
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, but the symbolic processor is not self consistent:
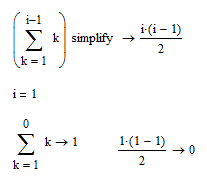
Edit:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard.
Yes, very inconsistent. Same issue appear sometimes with for loops, and are very hard to discover the 'error'. Point is which is the correct answer for that. For me, mupad and mathcad are bad. Wolfram alpha says that it is zero, not one:
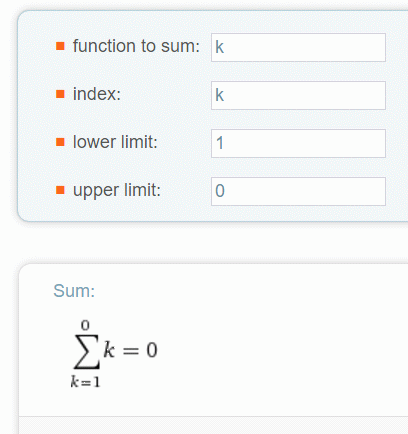
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't know if there is a convention for this, but if the assumption is that the upper limit must be greater then the lower limit the sum should return an error, not 0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, that's some radical. For integrals (and the integral symbol it's a S deformable) it is int(f,a,b) = - int(f,b,a). But for sums i guess, but not absolutely sure, that it is zero because there are nothing to add, then must to be zero.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, interesting point about integration. However, to me the sum from 0 to 1 should be the same as the sum from 1 to 0. It should not matter whether ones goes through the values of k in any particular order, because addition is commutative.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats the programmers view, not the mathematicians 😉
Unfortunately the implentation of the Fourier Sigma summation notation in Mathcad follows the programmers view of a simple for-loop which, from a mathematical point of view, simply is wrong.
In math we have the concept of the "empty sum" when the lower limit is larger than the upper one and it is defined to be zero. That way a lot of things can be presented in a very short way while otherwise would require some kind of case-by-case analysis. -> Empty sum - Wikipedia, the free encyclopedia
For some more in-depth reading about sums, summation notation and arithmetic with sums you may have a look at http://www.csie.ntu.edu.tw/~r97002/temp/Concrete%20Mathematics%202e.pdf
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fair enough. Then the sum from k=1 to 0 should not be allowed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Following the mathematical definition is should be allowed but should yield 0 as Alvaro already said.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner. That it is. "Empty sum". I remotely remember this convention, but don't do your research. It seems more than a bug than other thing in Mathcad.
Mupad is a German program, and have some others 'unusual' conventions, and someone's actually betters than american's. But for this case I don't know if there are a 'special' convention by the German mathematicians or it is just a bug in mupad, but guess that this is not the case.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
But for this case I don't know if there are a 'special' convention by the German mathematicians
Sure not. The problem seems that Mathcads numerics and also Mupad were implemented by programmers who thought that it undoubtedly (?) should be that way and the problem slipped by the consulting mathematicians.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There also are strange effects in other software, too.
While Mathacds numerics and muPad seem to agree on
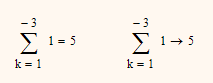
good old (really old) Derive thinks that the result should be -3

and Geogebras CAS agrees on
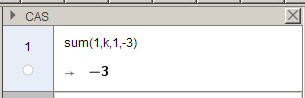
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
While Mathacds numerics and muPad seem to agree
I don't think that is certain. It's possible that someone noticed the discrepancy in the results, and somehow "fixed it" for certain calculations involving only numbers in the parser between Mathcad and MuPad. If so, then what they created is a discrepancy between MuPad and itself, depending on whether the expression is purely numeric or not. Since the Maple engine in MC11 gives the sum as zero my guess is that Mupad is indeed internally inconsistent, but without access to native MuPad there is no way to be sure.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi.
Ah, Derive, it's not dead, it's a Texas Instrument symbiont. But actually was never a good option.
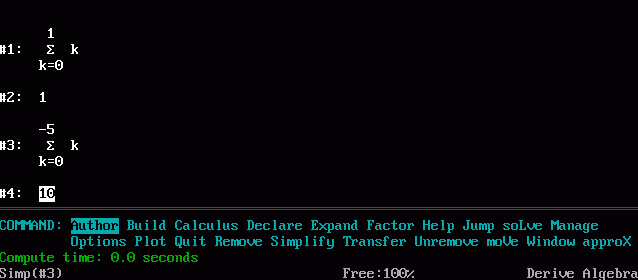
Richard suspicion it's right. Mupad implement an error over bad ranges.
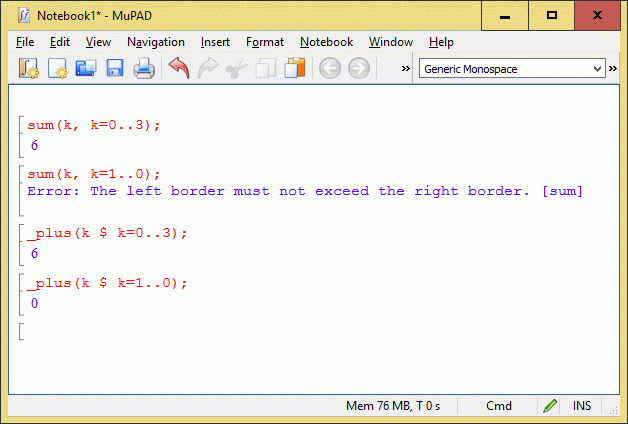
But while sum is very consistent, the recommended function for numerics have the 'usual' convention. MuPad is German, and those guys have their own set of conventions, which actually it's perfect to me. Too much uniformization can't be a good idea.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"Since the Maple engine in MC11 gives the sum as zero"
Not so sure about that. Here's mathcad 11:

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc.
Seems that maple's guys (french candian's, I guess) apply the convention for integrals:
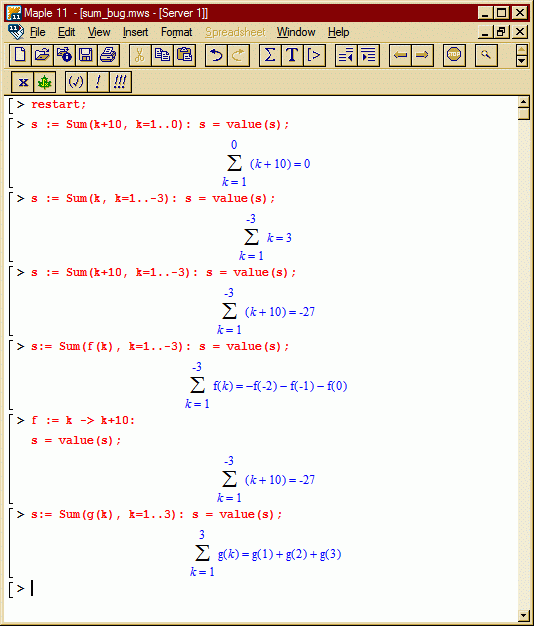
But also use some strange convention for how take the limits for the sums. ¿If there are 3 integers between the maple range 1..3, are also 3 integers between the range 1..-3?
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK. Maple gets the prize for weirdest of all! What logic do they use to come to the conclusion that the sum of f(k) from 1 to -3 is -f(-2)-f(-1)-f(0)? That makes no sense to me. What happened to f(-3) and f(1)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard.
As people says: "more was lost in the war". How much could be two single points? For an integral, you can take out a numerable set of single points without change the integral value; for instance, the interval limits. But for sums, don't seems a good practice. Mupad have the better assumption. Wolfram alpha too.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To put the example to the extreme (Mathcad 11):
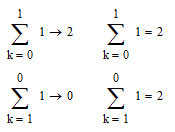
(Prime 3.1 Express, numeric only):

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks like Maple in Mathcad 11 followed the correct mathematical definition, while muPad (and Mathcads numerics) don't.
In MC15 the results are the same (wrong) ones regardless if you evaluate numeric or symbolic.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But at least then mathcad 15 provides consistent results (consistently wrong, OK, but consistent).
I got a different impression from the OP's description.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But at least then mathcad 15 provides consistent results (consistently wrong, OK, but consistent).
That's not the case. See my post above. If you symbolically simplify the sum and then evaluate symbolically, the result is 0. If you symbolically evaluate the sum the result is 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is still a discrepancy in Mathcad 15 symbolics
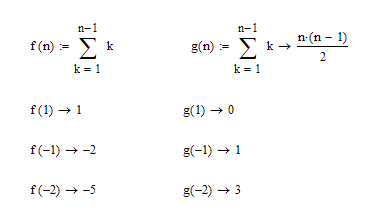
It should make no difference if you evaluate the expression symbolically before the function call.
Of course this would mean that the sum should only simplify to that expression if you add "assume,n>1,n=integer" which possibly would make everyday use a bit more cumbersome 🙂
Following the mathematically definition all results should be zero, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As there is in mathcad 11:

Wheras wolfram Alpha says:
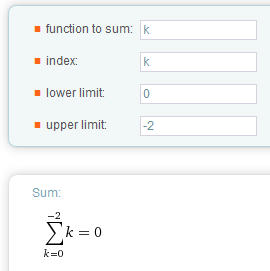
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you a lot for considering my issue and for the prompt answers.
I've started to write my problem in Mathcad in more detail, pretty much like Fred did above, but not finished since left for work.
After posting I've noticed too that there is a term in the beginning of the series with an upper limit of summation smaller than the lower limit and that might generate inconsistency or/and the error in numeric evaluation.
Best, Liv.





